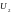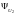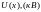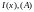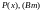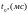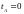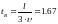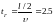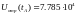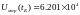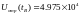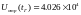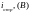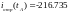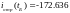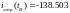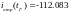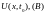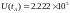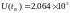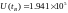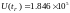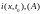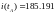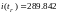МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИСТЕТ»

Инженерная школа энергетики

Отделение электроэнергетики и электротехники

Расчетно-графическая работа №6

Расчет длинных линий в установившемся и переходном режимах

Вариант 730

Исполнитель:
студент группы	5А8В		Воронина Е.А.
Руководитель:
к.т.н., доцент ОЭЭ ИШЭ			Шандарова Е.Б.

Томск 2020

ЗАДАНИЕ

Для одной фазы линии электропередачи длиной l = 1500 км и заданными удельными параметрами выполнить следующее:

1. В установившемся режиме при заданном фазном напряжении в конце линии

а ) определить волновое сопротивление Z_в, постоянную γ=α+jβ, фазовую скорость V, длину волны λ, комплексы действующих значений токов  напряжения  а также активные мощности в начале линии P₁ и конце линии P₂, эффективность передачи энергии по линии (КПД) 

б) изменяя координату x от 0 до l рассчитать распределение вдоль линии действующих значений напряжения U(x) и тока I(x), а также активной мощности P(x);

в) по результатам расчетов построить совмещенные графики зависимостей для действующих значений U(x) и I(x), а также активной мощности P(x).

2 . В переходном режиме при подключении линии без потерь (R₀  ≈ 0;G₀ ≈ 0) к источнику постоянного напряжения   рассчитать и построить совмещенные графики зависимостей распределения вдоль линии волн тока i(x, t₀) и напряжения u(x, t₀), соответствующих моменту времени   после подключения источника, когда отраженные от конца линии волны напряжения и тока достигли середины линии.

3. Проанализировать полученные результаты, графики зависимостей и сформулировать выводы по работе.

Исходные данные:

Таблица 1

№			R	L	C
-	кВ	град	Ом	Гн	мкФ
7	200	-45	400	1.27	7,69

Таблица 2

№	R0	L0	G0	C0
-	Ом/км	Гн/км	См/км	Ф/км
3	0.04	1.2*10-3	1,1*10-6	0.93*10-8

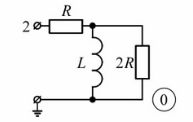
Рис. 1 Схема нагрузки линии

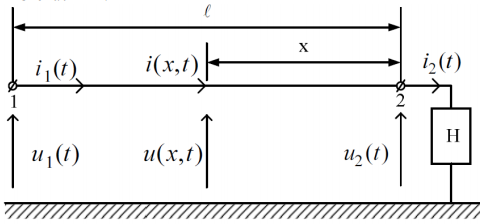
Рис. 2 Схема линии

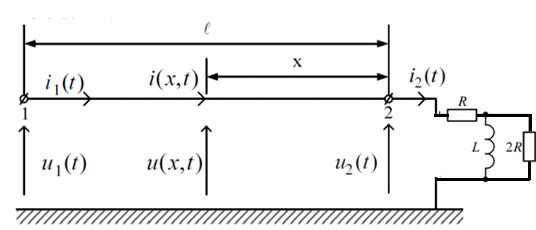
Рис. 3 Схема линии

1. В установившемся режиме при заданном фазном напряжении в конце линии

а ) определить волновое сопротивление Z_в, постоянную γ=α+jβ, фазовую скорость V, длину волны λ, комплексы действующих значений токов  напряжения  а также активные мощности в начале линии P₁ и конце линии P₂, эффективность передачи энергии по линии (КПД) 

Заданное фазное напряжение:

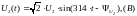
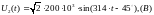
Определим в конце линии величины такие как:

Комплексное волновое сопротивление:

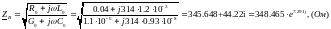
Постоянная распространения:

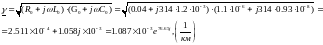
Коэффициент затухания α и коэффициент фазы β:

Фазовая скорость:

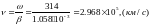
Длина волны:

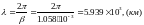
Комплексное сопротивление нагрузки при комплексном сопротивлении ёмкости:

Сопротивление нагрузки будет равно эквивалентному сопротивлению схемы нагрузки, которая изображена на рис. 1:

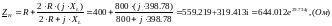
Комплекс действующего значения тока в нагрузке по закону Ома:

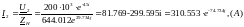
Комплексные постоянные интегрирования:

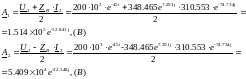
Комплексы действующих значений напряжения и тока в начале линии

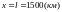
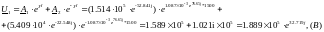
Найдем активные мощности в конце линии и начале:

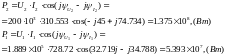
Эффективность передачи энергии по линии:

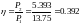
б) изменяя координату x от 0 до 1500 рассчитать распределение вдоль линии действующих значений напряжения U(x) и тока I(x), а также активной мощности P(x);

Используя уравнения:

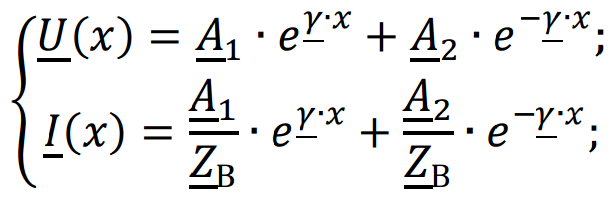
рассчитаем действующие значения напряжения 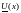и тока 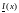, а так же активную мощность . Результаты расчетов занесем в таблицу 3:

Таблица 3

x, км	0	300	600	900	1200	1500
	200	213.2	212.7	202.7	191.1	188.9
	310.553	325.753	416.553	534.704	644.66	728.72
	5.393*10^7	6.935*10^7	8.608*10^7	1.031*10^8	1.201*10^8	1.375*10^8

в) по результатам расчетов построить совмещенные графики зависимостей для действующих значений U(x) и I(x), а также активной мощности P(x).

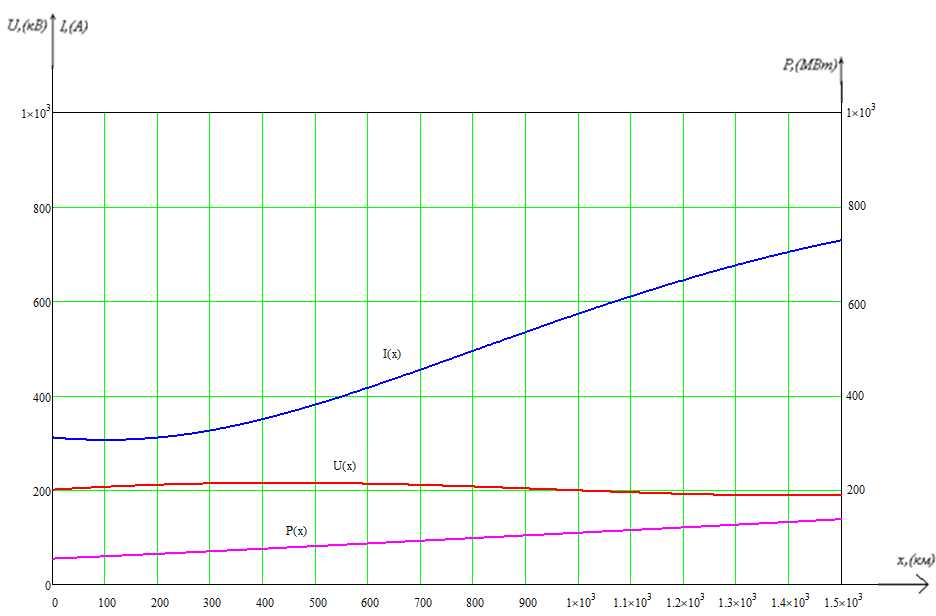
Рис.3- Зависимости

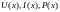
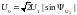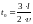2. В переходном режиме при подключении линии без потерь (R₀  ≈ 0;G₀ ≈ 0) к источнику постоянного напряжения рассчитать и построить совмещенные графики зависимостей распределения вдоль линии волн тока i(x, t₀) и напряжения u(x, t₀), соответствующих моменту времени  после подключения источника, когда отраженные от конца линии волны напряжения и тока достигли середины линии.

Источник постоянного напряжения:

Волновое сопротивление:

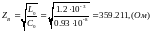
Фазовая скорость:

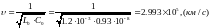
Определим падающие волны напряжения и тока:

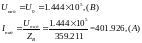
Найдем напряжение 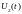и ток 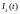в нагрузке, воспользовавшись классическим методом для цепи первого порядка:

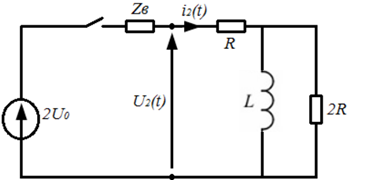
Рис.4 – Схема для нахождения мгновенных значений тока и напряжения в конце линии

• Находим ННУ при t=0_{_}.

Так как ключ еще не сработал, то в цепи нет ни тока ни напряжения, следовательно

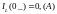
• Теперь находим ЗНУ при t=0₊.

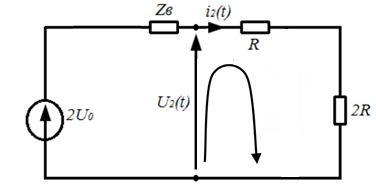
Рис.5 – Схема для нахождения ЗНУ

Ключ уже сработал, 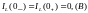, а это означает что мы получим разрыв (рис.5)

Рассчитаем ток, используя закон Ома:

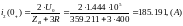
Теперь найдем напряжение, используя II закон Кирхгофа и обойдя контур как указано на рис.5:

• Определяем принужденную составляющую при t=∞

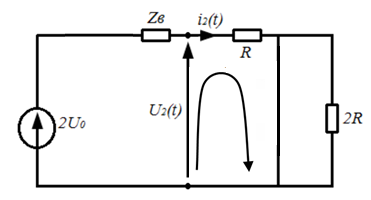
Рис.6 – Схема для нахождения принужденной составляющей

Схема после коммутации, установившийся режим, конденсатор будет разрывом (рис.6), находим ток как и в прошлом пункте используя закон Ома:

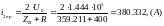
Напряжение аналогично напряжению ЗНУ найдем через II закон Кирхгофа взяв контур обхода, который указан на рис.6:

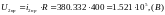
• Определяем корень характеристического уравнения

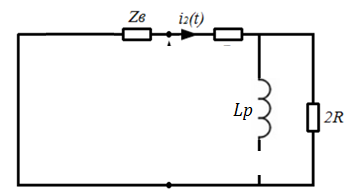
Рис.7 – Схема для нахождения корня характеристического уравнения

Для получения схемы заменяем источник ЭДС на закоротку, а конденсатор обозначаем 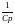и делаем разрыв (желательно в месте реактивного сопротивления, так будет удобнее считать полное сопротивление). Находим полное сопротивление и приравниваем к нулю:

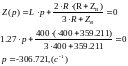
• Находим постоянные интегрирования:

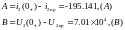
• Записываем конечный результат:

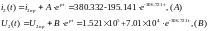
Отраженные от конца линии волны напряжения будут иметь вид:

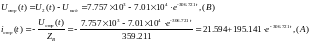
Рассчитываем распределение напряжения и тока вдоль линии для момента времени:

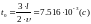, после подключения источника, когда отраженные от конца линии волны напряжения и тока достигли середины линии. Для этого заполним таблицу 4:

Таблица 4

Точка	А Середина линии	Б	В	Г Нагрузка

Теперь построим графики для :

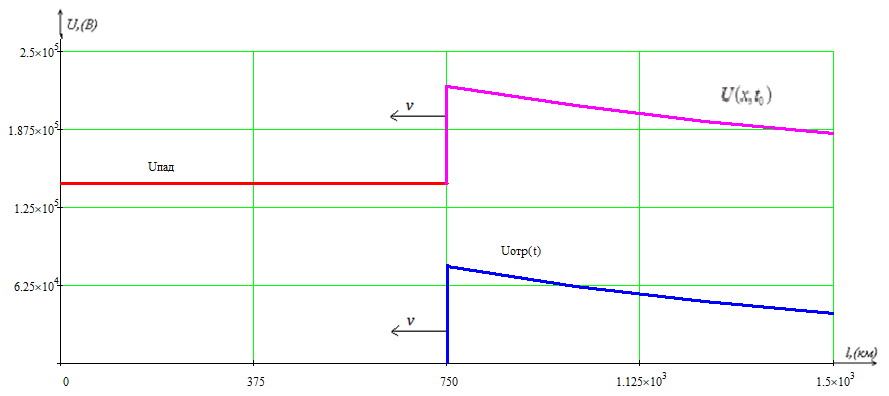
Рис.8 – напряжения в различных точках линии

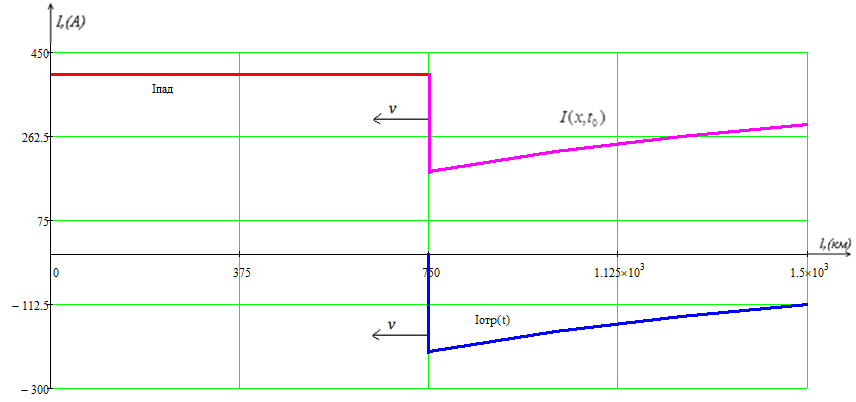
Рис.9 – Токи в различных точках линии

3. Проанализировать полученные результаты, графики зависимостей и сформулировать выводы по работе.

Вывод: в ходе решения задания в установившемся режиме при заданном фазном напряжении в конце линии были рассчитаны следующие параметры: волновое сопротивление, постоянная распространения, фазовая скорость, длина волны, комплексы действующих значений и токов и напряжения, а также активные мощности в начале и конце линии и КПД. Также были построены зависимости U(x), I(x) и P(x): изменение напряжения и тока вдоль линии в функции x обусловлено наличием продольных сопротивлений и поперечных проводимостей, а активная мощность P монотонно убывает к концу линии.

В переходном режиме при подключении линии без потерь к источнику постоянного напряжения были рассчитаны законы изменения тока i(x, to) и напряжения u(x, to) для соответствующего момента времени после подключения источника, когда отраженные от конца линии волны напряжения и тока достигли середины линии и построен график распределения напряжения и тока вдоль линии для этого момента времени. В каждой точке линии напряжение и ток равны сумме падающих и отраженных волн, которые запаздывают во времени относительно соответственно начала и конца линии.

Также были выявлены значения напряжений и токов, которые должны выдержать изоляция и площадь сечения провода:

В установившемся режиме Umax=213,2кВ при x=300км (конец линии), Umin=188,9кВ при x=900 км (начало линии), Imax=728.72А при x=1500 км (конец линии), Imin=310.553кА при x=0 км.

В переходном режиме Umax= В в точке А (середина линии), Umin= В в точке Г (нагрузка), Imax= А в точке Г (нагрузка), Imin= А в точке А (середина линии)