Добавил:

Shanie Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Авиационный Технический Университет

Предмет:

Организация и планирование производства

Файл:

Лабораторные / ЛР3 Игры с природой

.docx

Скачиваний:

Добавлен:

13.11.2021

Размер:

52.21 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

ФГБОУ ВО

Уфимский государственный авиационный технический университет

Кафедра УИ

Отчёт

по лабораторной работе №3

по дисциплине «Организация и планирование производства»

Тема: «Игры с природой»

Выполнил: ст. гр. И-208

Исламова Р. Р.

Принял: к. э. н., доц.

Кузнецова Н. П.

Уфа 2021 г.

Цель работы: изучение специальных критериев Вальда, Сэвиджа, Гурвица и Лапласа для принятия решения в условиях неопределённости природы.

Задача 1

Решается вопрос о выпуске телевизоров при различных предположениях о ёмкости рынка. Критерием выбора стратегии выпуска является максимальная прибыль. Известны вероятности различных значений ёмкости рынка, образующих полную группу взаимоисключающих событий P_j (с вероятностью P₁ = 0,1 купят А₁ шт. телевизоров; с вероятностью P₂ = 0,2 купят А₂шт. телевизоров; с вероятностью P₃ = 0,5 купят А₃ шт. телевизоров; с вероятностью P₄ = 0,2 купят А₄ шт. телевизоров; 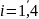). Определить, используя критерии Вальда, Сэвиджа, Гурвица и Лапласа, оптимальную стратегию предприятия (таблица 1).

Таблица 1 – Исходные данные к задаче 1

№	А₁, тыс. шт.	А₂, тыс. шт.	А₃, тыс. шт.	А₄, тыс. шт.	Отпускная цена телевизора Ц, у. е.	Полные затраты на производство телевизора С, у. е.
1	100	200	300	400	100	50
2	105	205	305	405	150	70
3	95	190	290	380	130	60
4	80	210	310	405	120	55

Внесём в таблицу данные о прогнозируемой прибыли за продажу телевизоров. Данные приведены в таблице 2.

Таблица 2 – Прогнозируемая прибыль

№	А₁, тыс. у. е.	А₂, тыс. у. е.	А₃, тыс. у. е.	А₄, тыс. у. е.
1	10000	20000	30000	40000
2	15750	30750	45750	60750
3	12350	24700	37700	49400
4	9600	25200	37200	48600

Решение

Критерий Лапласа предполагает, что все состояния природы равновероятны. Тогда при j = 4 p = 1/4 = 0,25.

Рассчитаем прибыль с учётом вероятности, тогда для стратегий 1-4 получим прибыль, равную:

1 – 25 000 у. е.;

2 – 38 250 у. е.;

3 – 31 037 у. е.;

4 – 30 150 у. е.

Как видим, по критерию Лапласа наиболее выгодной является стратегия 2, так как её реализация принесёт наибольшую прибыль.

Критерий Гурвица используем минимумы и максимумы строк. Внесём их в таблицу 3.

Таблица 3 – Данные для критерия Гурвица

Стратегия	Минимум строк	Максимум строк	А (минимум строк) + (1 – α) (максимум строк)
1	10000	40000	25000
2	15750	60750	38250
3	12350	49400	30875
4	9600	48600	29100

При α = 0,5 максимальная прибыль получается при стратегии 2.

Критерий Сэвиджа. Матрица для критерия представлена в таблице 4.

Таблица 4 – Матрица затрат для критерия Сэвиджа

Стратегия	А₁	А₂	А₃	А₄	Максимум строк
1	400	0	0	0	400
2	6150	10750	15750	20750	20750
3	2750	4700	7700	9400	9400
4	0	5200	7200	8600	8600

При решении задачи по критерию Сэвиджа наименее рискованной, следовательно, наиболее оптимальной является стратегия 1.

Критерий Вальда. Используем максиминный критерий, так как результат оценивается по итоговой прибыли. Результаты решения представлены в таблице 5.

Таблица 5 – Матрица для критерия Вальда

Стратегия	А₁	А₂	А₃	А₄	Минимум строк
1	10000	20000	30000	40000	10000
2	15750	30750	45750	60750	15750
3	12350	24700	37700	49400	12350
4	9600	25200	37200	48600	9600

Максимином в данной задаче является стратегия 2.

Таким образом, по трём из четырёх критериев наиболее оптимальной стратегией является стратегия 2.

Задача 2

На вновь организованную выставку требуется набрать экскурсоводов. Каждый экскурсовод может провести 4 экскурсии в день (каждая экскурсия по 25 человек). Известны затраты на содержание выставки в день, зарплата экскурсовода в день, цена билета. Ежедневно выставку могут посетить 50, 100, 150, 200, 250, 300 человек. Найти оптимальное число экскурсоводов для работы на выставке, используя критерии Вальда, Сэвиджа, Гурвица и Лапласа (таблица 2).

Таблица 6 – Исходные данные к задаче 2

№ варианта	Затраты на содержание выставки, руб/день	З/п экскурсовода, руб/день	Цена билета, руб
1	80	40	2
2	85	45	7
3	90	50	10
4	95	55	15

Решение

Максимально возможное число экскурсоводов – 3. Будем считать, что оплату каждый получает за день, т. е. вне зависимости от количества проведённых экскурсий. Тогда матрица прибыли в каждом случае примет вид, как в таблице 7.

Таблица 7 – Матрица прибыли к задаче 2

Стратегия	50	100	150	200	250	300
1 (1 экс.)	-20	80	20	-80	-140	-240
2 (1 экс.)	220	570	265	-85	-390	-740
3 (1 экс.)	360	860	410	-90	-540	-1040
4 (1 экс.)	600	1350	655	-95	-790	-1540
1 (2 экс.)	-60	40	140	240	180	0
2 (2 экс.)	175	525	875	1225	920	480
3 (2 экс.)	310	810	1310	1810	1360	760
4 (2 экс.)	545	1295	2045	2795	2100	1240
1 (3 экс.)	-100	0	100	200	300	400
2 (3 экс.)	130	480	830	1180	1530	1880
3 (3 экс.)	260	760	1260	1760	2260	2760
4 (4 экс.)	490	1240	1990	2740	3490	4240

Критерий Лапласа. Для шести вариантов состояния природы p = 0,17. Тогда матрица примет вид, как в таблице 8.

Таблица 8 – Матрица для критерия Лапласа

Стратегия	50	100	150	200	250	300	Прибыль
1 (1 экс.)	-20	80	20	-80	-140	-240	-63,33
2 (1 экс.)	220	570	265	-85	-390	-740	-26,67
3 (1 экс.)	360	860	410	-90	-540	-1040	-6,67
4 (1 экс.)	600	1350	655	-95	-790	-1540	30,00
1 (2 экс.)	-60	40	140	240	180	0	90,00
2 (2 экс.)	175	525	875	1225	920	480	700,00
3 (2 экс.)	310	810	1310	1810	1360	760	1060,00
4 (2 экс.)	545	1295	2045	2795	2100	1240	1670,00
1 (3 экс.)	-100	0	100	200	300	400	150,00
2 (3 экс.)	130	480	830	1180	1530	1880	1005,00
3 (3 экс.)	260	760	1260	1760	2260	2760	1510,00
4 (4 экс.)	490	1240	1990	2740	3490	4240	2365,00

Как видно из матрицы, в большинстве стратегий с наймом одного экскурсовода итогом являются убытки, следовательно, уже на этом этапе считаем, что один экскурсовод невыгоден. Максимальная прибыль наблюдается при использовании стратегии 4 с наймом троих экскурсоводов.

Критерий Гурвица. Рассчитаем значения при α = 0,5. Результаты расчётов представлены в таблице 9.

Таблица 9 – Расчёты по критерию Гурвица

Стратегия	Минимум строк	Максимум строк	А(минимум строк) + +(1 – α) (максимум строк)
1 (1 экс.)	-240	80	-80
2 (1 экс.)	-740	570	-85
3 (1 экс.)	-1040	860	-90
4 (1 экс.)	-1540	1350	-95
1 (2 экс.)	-60	240	90
2 (2 экс.)	175	1225	700
3 (2 экс.)	310	1810	1060
4 (2 экс.)	545	2795	1670
1 (3 экс.)	-100	400	150
2 (3 экс.)	130	1880	1005
3 (3 экс.)	260	2760	1510
4 (4 экс.)	490	4240	2365

При α = 0,5 максимальная прибыль также наблюдается при использовании стратегии 4 с наймом троих экскурсоводов.

Критерий Сэвиджа. Рассчитаем значения для матрицы затрат. Результаты представлены в таблице 10.

Таблица 10 – Матрица для критерия Сэвиджа

Стратегия	50	100	150	200	250	300	Максимум строк
1 (1 экс.)	80	80	0	15	650	1300	1300
2 (1 экс.)	320	570	245	10	400	800	800
3 (1 экс.)	460	860	390	5	250	500	860

Продолжение таблицы 10

Стратегия	50	100	150	200	250	300	Максимум строк
4 (1 экс.)	700	1350	635	0	0	0	1350
1 (2 экс.)	40	40	120	335	970	1540	1540
2 (2 экс.)	275	525	855	1320	1710	2020	2020
3 (2 экс.)	410	810	1290	1905	2150	2300	2300
4 (2 экс.)	645	1295	2025	2890	2890	2780	2890
1 (3 экс.)	0	0	80	295	1090	1940	1940
2 (3 экс.)	230	480	810	1275	2320	3420	3420
3 (3 экс.)	360	760	1240	1855	3050	4300	4300
4 (4 экс.)	590	1240	1970	2835	4280	5780	5780

При решении задачи с помощью критерия Сэвиджа наименее рискованным является стратегия 2 с одним экскурсоводом.

Критерий Вальда. Используем максиминный критерий, так как результат оценивается по итоговой прибыли. Результаты решения представлены в таблице 11.

Таблица 11 – Таблица для критерия Вальда

Стратегия	50	100	150	200	250	300	Минимум строк
1 (1 экс.)	-20	80	20	-80	-140	-240	-240
2 (1 экс.)	220	570	265	-85	-390	-740	-740
3 (1 экс.)	360	860	410	-90	-540	-1040	-1040
4 (1 экс.)	600	1350	655	-95	-790	-1540	-1540
1 (2 экс.)	-60	40	140	240	180	0	-60
2 (2 экс.)	175	525	875	1225	920	480	175
3 (2 экс.)	310	810	1310	1810	1360	760	310
4 (2 экс.)	545	1295	2045	2795	2100	1240	545
1 (3 экс.)	-100	0	100	200	300	400	-100
2 (3 экс.)	130	480	830	1180	1530	1880	130
3 (3 экс.)	260	760	1260	1760	2260	2760	260
4 (4 экс.)	490	1240	1990	2740	3490	4240	490

1 / 21 2 > Следующая >>>

Соседние файлы в папке Лабораторные

#
13.11.202137.54 Кб6ЛР1 Развитие производственной мощности предприятия.docx
#
13.11.202117.76 Кб8ЛР1 Расчёты.xlsx
#
13.11.2021153.36 Кб4ЛР2 Выбор решения в условиях неопределённости.docx
#
13.11.202152.21 Кб5ЛР3 Игры с природой.docx
#
13.11.202119.72 Кб5ЛР3 Расчёты.xlsx
#
13.11.202145.56 Кб5ЛР4 Метод принятия решения.docx