1. Fcm алгоритм нечіткої кластеризації
Алгоритм нечіткої кластеризації називають FCM-алгоритмом (Fuzzy Classifier Means, Fuzzy C-Means). Метою FCM-алгоритму кластеризації є автоматична класифікація множини об'єктів, які задаються векторами ознак в просторі ознак. Іншими словами, такий алгоритм визначає кластери і, відповідно, класифікує об'єкти. Кластери представляються нечіткими множинами і, крім того, межі між кластерами також є нечіткими.
FCM-алгоритм кластеризації припускає, що об'єкти належать всім кластерам з певною ФП. Ступінь приналежності визначається відстанню від об'єкту до відповідних кластерних центрів. Даний алгоритм ітеративно обчислює центри кластерів і нові ступені приналежності об'єктів.
Для
заданої множини K
вхідних
векторів
і N
кластерів
,
що виділяються, передбачається, що
будь-який
належить будь-якому
із ступенем приналежності,
де
j
– номер кластера, а k
– вхідного вектора.
Приймаються до уваги наступні умови нормування:
Мета алгоритму полягає в мінімізації суми всіх зважених відстаней
де q– фіксований параметр, що задається перед ітераціями.
Для досягнення вищезгаданої мети необхідно розв’язати наступну систему рівнянь:
Спільно
з умовами нормування
дана система диференціальних рівнянь
має наступний розв’язок:
(зважений центр тяжіння (center of gravity – cog)) і
2. Розв’язання задачі нечіткої кластеризації з використанням MatLab методом fcm
У системі MatLab для розв’язання завдання нечіткої кластеризації на основі алгоритму FCM може бути використаний спеціальний графічний інтерфейс кластеризації, що викликається функцією findcluster. Розглянемо особливості його застосування.
Функція findcluster призначена для виклику графічного інтерфейсу програми нечіткої кластеризації для методу нечітких с-середніх і методу субтрактивної кластеризації (subtractive clustering). Вона може бути викликана в одному з наступних форматів: findcluster або findcluster('file.dat'). У першому випадку функція findcluster викликає графічний інтерфейс GUI програми для виконання нечіткої кластеризації алгоритмом FCM і/або нечіткій субтрактивної кластеризації. При цьому необхідно завантажити в робочу область початкові дані із зовнішнього файлу за допомогою кнопки Load Data (рис. 4.1).
Рис. 4.1.
У другому випадку функція findcluster('file.dat') викликає графічний інтерфейс, а в робочу область автоматично завантажуються дані кластеризації із зовнішнього файлу file.dat. При цьому на графіку відображаються значення матриці даних для перших двох ознак. Результат із завантаженими початковими даними із зовнішнього файлу fcmdata.dat представлений на рис. 4.2.
Рис. 4.2.
Вибір методу нечіткої кластеризації здійснюється за допомогою списку Methods. Для кожного з методів нечіткої кластеризації у відповідних рядках введення встановлені значення параметрів алгоритмів за умовчанням. В цьому випадку вони мають наступні значення:
- Cluster Num: число шуканих нечітких кластерів с, дорівнює с=2;
- Max Iteration#: максимальне число ітерацій s, дорівнює s=100;
- Min Improvement: параметр збіжності алгоритму е, дорівнює е=0.00001;
- Exponent: експоненціальна вага m для розрахунку матриці нечіткого розбиття, дорівнює m=2.
Ці значення можуть бути змінені користувачем. Для цього необхідно встановити курсор введення у відповідне поле і набрати потрібні цифри з урахуванням допустимих значень параметрів.
Після натиснення на кнопку Start починає роботу відповідний алгоритм нечіткої кластеризації з параметрами, встановленими за умовчанням або зміненими користувачем. Результати роботи алгоритму відображаються на графіку (рис. 4.3). Знайдені центри кластерів зображені чорними квадратиками, і їх координати можна зберегти в зовнішньому файлі з метою подальшого аналізу, натиснувши кнопку Save Center…
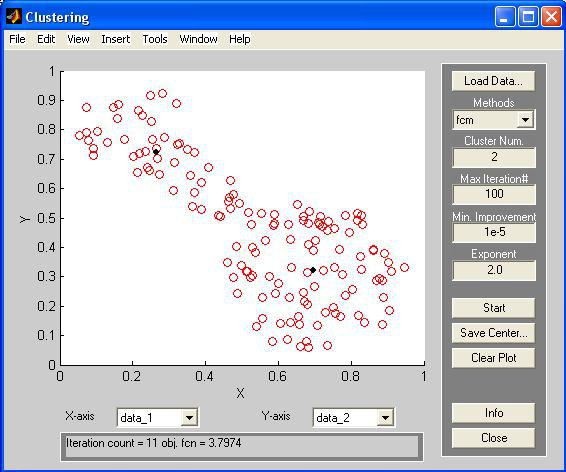
Рис. 4.3.
Параметр iteration count показує кількість ітерацій, а obj.fcn – відповідне значення цільової функції.