Типи функцій приналежності, що використовуються в системі SciLab

Для роботи з fuzzy logic потрібно завантажити модуль SciFLT в систему SciLAB. Зробити це можна відкривши файл loader.sce з цього пакету і виконавши команду execute-> load into SciLAB.

Інструментарій нечіткої логіки (ІНЛ) у складі пакету SciFLT містить 11 вбудованих типів функцій приналежності (ФП), що формуються на основі кусково-лінійних функцій, розподілу Гауса, сигмоїдної кривої, квадратичних і кубічних поліноміальних кривих.

До найбільш простих ФП (і в цьому їх головне достоїнство) можна віднести трикутну і трапецієвидну. Найменування трикутної ФП – trimf (triangle membership function). У параметричному вигляді вона є ні що інше, як набір трьох крапок, що створюють трикутник.

Опис функції: у = trimf(x [а b с]), де вектор x позначає базову множину, на якій визначається ФП, величини а і с задають основу трикутника, b – його вершину.

У аналітичному вигляді трикутна ФП може бути задана таким чином:

Далі розглянемо приклади використання різних ФП в системі SciFLT. Прикладами є фрагменти програм і коментарів на мові пакету SciLAB.

Приклад 1. Програма використання ФП trimf (результат на рис.1).

x=linspace(0,1,100)'; //задаємо множину х

y1=trimf(x[0 0.2 0.4]); //і три трикутні функції на ньому

y2=trimf(x[0.2 0.5 0.9]);

y3=trimf(x[0.5 0.6 0.9 ]);

xbasc();

//будуємо функції приналежності

plot2d(x,[y1 y2 y3],leg="y1@y2@y3");

//підписуємо рисунок

xtitle("Triangular Member Function Example","x","mu(x)");

Символ “ ' ” у рядку визначення базової множини x показує транспонованість базової множини.

Рис. 1. Трикутні функції приналежності

Трапецієвидна ФП, trapmf (trapezoid membership function), відрізняється від попередньої функції лише тим, що має верхню основу.

Опис функції: у = trаpmf(x [а b с d]), де параметри а і d задають нижню основу, b і с – верхню основу трапеції.

Аналітичний запис трапецієвидної функції має вигляд:

Рис. 2. Трапецієвидні функції приналежності

Приклад 2. Програма використання ФП trapmf (результат на Рис. 2).

x=linspace(0,1,100)';

y1=trapmf(x[0 0.2 0.4 0.6]);

y2=trapmf(x[0.2 0.5 0.6 0.9]);

y3=trapmf(x[0.5 0.6 0.8 0.9 ]);

xbasc(); plot2d(x,[y1 y2 y3],leg="y1@y2@y3");

xtitle("Trapezoidal Member Function Example","x","mu(x)");

Символ “ ' ” у рядку визначення базової множини x показує транспонованість базової множини.

На основі функції розподілу Гауса в SciFLT можна побудувати ФП двох видів: просту ФП Гауса і двосторонню ФП, утворену за допомогою різних функцій розподілу Гауса. Перша з них позначається – gaussmf, а друга – gauss2mf.

Опис функції: у = gaussmf(x [σ с]).

Симетрична функція Гауса залежить від двох параметрів σ і с:

Опис двосторонньої функції приналежності: y = gauss2mf(x, [σ₁ c₁ σ₂ c₂]).

Останній вираз є комбінацією двох різних функцій розподілу Гауса. Перша визначається параметрами σ₁ і c₁ і задає форму лівої сторони, а друга (параметри σ₂ і c₂) – правої сторони ФП.

Якщо c₁ < c₂, то в цьому випадку функція gauss2mf досягає свого максимального значення на рівні 1. Інакше – максимальне значення функції менше 1.

На рис. 3. представлені графіки кривих gaussmf і gauss2mf, заданих в програмі з прикладу 3.

Рис. 3. Гаусові криві

Приклад 3. Програма використання ФП gaussmf.

x=linspace(0,1,100)';

y1=gaussmf(x[0.3 0.1]);

y2=gauss2mf(x[0.2 0.1 0.5 0.2]); xbasc();

plot2d(x,[y1 y2],leg="y1@y2");

xtitle("Gaussian Member Function Example","x","mu(x)");

Символ “ ' ” у рядку визначення базової множини x показує транспонованість базової множини.

Наступною функцією, яка дозволяє представляти нечіткі суб'єктивні переваги, є ФП «узагальнений дзвін». Вона позначається gbellmf (bell shape membership function). Її відмінність від розглянутих раніше ФП полягає в додаванні третього параметру, що дозволяє здійснювати плавний перехід від нечіткої множини до чіткої.

Опис функції: y = gbellmf(x, [a b c]).

Функція «узагальнений дзвін» має наступний аналітичний вигляд:

,

де с визначає розташування центру ФП, а і b впливають на форму кривої (рис. 4).

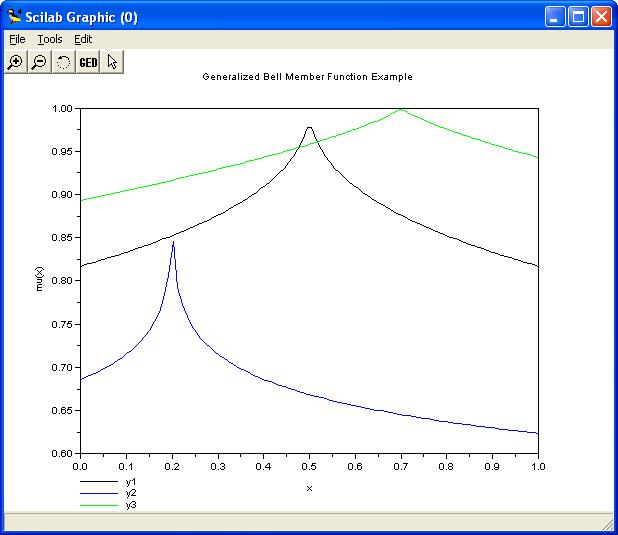
Рис. 4. Дзвіноподібні функції приналежності

Приклад 4. Програма використання gbellmf (результат на рис. 4).

x=linspace(0,1,100)';

y1=gbellmf(x[0.5 10 0.5]);

y2=gbellmf(x[0.2 10 0.2]);

y3=gbellmf(x[0.7 10 0.8]);

xbasc();

plot2d(x,[y1 y2 y3],leg="y1@y2@y3");

xtitle("Generalized Bell Member Function Example","x","mu(x)");

Символ “ ' ” у рядку визначення базової множини x показує транспонованість базової множини.

ФП на основі функції розподілу Гауса і ФП «узагальнений дзвін» відрізняються гладкістю і простотою запису і є найбільш використовуваними при описі нечітких множин.

Але не дивлячись на те, що гаусові і дзвіноподібні ФП мають властивість гладкості, вони не дозволяють формувати асиметричні ФП. Для цих цілей в SciFLT існує набір сигмоїдних функцій, які можуть бути відкриті або зліва, або справа в залежності від типу функції. Симетричні і закриті функції синтезують з використанням двох додаткових сигмоїдів. Основна сигмоїдна ФП позначається sigmf, а додаткові – dsigmf і psigmf.

Опис основної сигмоидной функції: y = sigmf(x, [a c]).

У аналітичній формі сигмоїдна функція sigmf записується таким чином:

.

Залежно від знаку параметра а дана ФП буде відкрита справа або зліва (рис. 5), що дозволяє застосовувати її при описі таких нечітких понять, як «дуже великий», «вкрай негативно» і тому подібні.

Опис додаткової сигмоїдної функції: y= dsigmf(x, [a₁ c₁ a₂ c₂]).

ФП dsigmf залежить від чотирьох параметрів a₁, c₁, a₂, c₂ і визначається як різниця двох сигмоїдних функцій: f₁(x,a₁,c₁) – f₂(x,a₂,c₂).

Опис додаткової сигмоїдної функції: y = psigmf(x,[a₁ c₁ a₂ c₂]).

ФП psigmf також як і попередня функція залежить від чотирьох параметрів a₁, c₁, a₂, c₂ і визначається як твір два сигмоїдних функцій: f₁(x,a₁,c₁)*f₂(x,a₂,c₂).

Рис. 5. Сигмоїдні функції приналежності

Приклад 5. Програма використання сигмоїдних функцій (результат на рис. 5).

x=linspace(0,1,100)';

sig1=sigmf(x[12 0.3]);

sig2=sigmf(x[ -12 0.7]);

psig=psigmf(x[15 0.5 -15 0.7]);

dsig=dsigmf(x[15 0.1 15 0.3]); xbasc();

plot2d(x,[sig1 sig2 psig dsig],leg="sig1@sig2@psig@dsig");

xtitle("Sigmoidals Member Functions Examples","x","mu(x)");

Символ “ ' ” у рядку визначення базової множини x показує транспонованість базової множини.

Інструментарій нечіткої логіки SciFLT дає можливість формування ФП на основі поліноміальних кривих. Відповідні функції називаються Z-функції (zmf), PI-функції (pimf) і S-функції (smf). Функція zmf є асиметричною поліноміальною кривою, відкритою зліва, функція smf – дзеркальне відображення функції zmf. Функція pimf дорівнює нулю в правій і лівій межах і приймає значення, що дорівнює одиниці в середині деякого відрізку (рис. 6).

Опис функції: у = zmf(x [а b]).

Параметри а і b визначають екстремальні значення кривої.

Опис функції: у = pimf(x [а b с d]).

Параметри а і d задають перехід функції в нульове значення, параметри b і с – в одиничне.

Опис функції: у = smf(x [а b]).

Параметри а і b визначають екстремальні значення кривої.

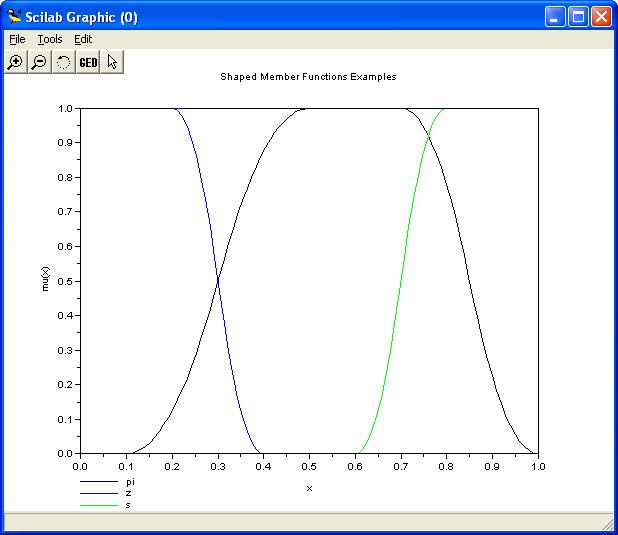
Рис. 6.Поліноміальні криві

Приклад 6. Програма використання поліноміальних кривих (результат на рис. 6).

x=linspace(0,1,100)';

pi=pimf(x[0.1 0.5 0.7 1.0]);

z=zmf(x[0.2 0.4]);

s=smf(x[0.6 0.8]);

xbasc();

plot2d(x,[pi z s],leg="pi@z@s");

xtitle("Shaped Member Functions Examples","x","mu(x)");

Символ “ ' ” у рядку визначення базової множини x показує транспонованість базової множини.

Крім розглянутих вище функцій, що дозволяють представляти нечіткі множини, в SciFLT можна формувати власні ФП або модифікувати вбудовані.