Міністерство освіти і науки України

Харківський національний університет радіоелектроніки

МЕТОДИЧНІ ВКАЗІВКИ

до лабораторних робіт

з дисципліни

"НЕЧІТКІ МНОЖИНИ"

для підготовки магістрів усіх форм навчання

спеціальності 122 − Комп’ютерні науки

галузі знань 12 − Інформаційні технології

Електронне видання

Затверджено

кафедрою "Штучного інтелекту"

Протокол № ___ від "__" __________ 2018 р.

Харків 2018

Методичні вказівки до лабораторних робіт з дисципліни "Нечіткі множини" для підготовки фахівців освітньо-кваліфікаційного рівня магістр за спеціальністю 122 – Комп’ютерні науки [Електронне видання] / Упоряд. К.Е. Петров. – Харків: ХНУРЕ, 2018 – 57 с.

Упорядник К.Е. Петров

Зміст

Вступ……………………………………………..…….……….……..….…….3

Лабораторна робота № 1…………………………...………………...….….....6

Лабораторна робота № 2…………………………………..….……………...10

Лабораторна робота № 3……………………….…..………………….....…..21

Лабораторна робота № 4……………………….…..……………….…....…..25

Рекомендована література …………………………..……………………....57

ВСТУП

Сьогодні нечітка логіка розглядається як стандартний метод моделювання і проектування. У 1997 р. мова нечіткого управління (Fuzzy Control Language) внесена до Міжнародного стандарту програмованих контролерів IЕС 1131-7. Системи на нечітких множинах розроблені і успішно упроваджені в таких областях, як: медична діагностика, технічна діагностика, фінансовий менеджмент, управління персоналом, біржове прогнозування, розпізнавання образів, розвідка копалин, виявлення шахрайств, управління комп'ютерними мережами, управління технологічними процесами, управління транспортом, логістика, пошук інформації в Інтернеті, радіозв'язок і телебачення. Спектр додатків дуже широкий – від побутових відеокамер, пилососів і пральних машин до засобів наведення ракет ППО і управління бойовими вертольотами і літаками. Як і раніше лідирує Японія, в якій випущено понад 4800 «нечітких» патентів (для порівняння, в США їх близько 1700). Практичний досвід розробки систем на нечітких множинах свідчить, що терміни і вартість їх проектування значно нижчі, ніж при використанні традиційного математичного апарату, при цьому забезпечуються необхідні рівні якості. Отець нечіткої логіки Лотфі Заде якось із цього приводу відмітив, що «майже завжди можна зробити такий же самий продукт без нечіткої логіки, але з нечіткою буде швидше і дешевше».

Мета дисципліни полягає у вивченні теоретичних основ та практичних аспектів використання нечітких методів інтелектуальних обчислень для проектування систем штучного інтелекту; отримання студентами теоретичних і практичних знань щодо основ теорії нечітких множин і систем, алгоритмів нечіткого логічного виведення з метою застосування цих знань для розробки алгоритмічного і програмного забезпечення технічних і інформаційних інтелектуальних систем, в умовах відсутності докладного і однозначного опису зовнішнього середовища; формування у студентів з теоретичних і практичних навичок щодо створення сучасних інтелектуальних систем підтримки прийняття рішень і нечітких систем управління складними системами.

За результатами вивчення дисципліни студенти повинні:

знати: концепції теорії нечітких множин (НМ) та галузі їх застосування в системах обчислювального інтелекту; основні принципи нечіткої логіки і нечітких обчислень; алгоритми нечіткого логічного виведення Мамдані, Такагі-Сугено-Канга (ТСК) та ін. і принципіи їх застосування при створенні сучасних інформаційних інтелектуальних систем; стратегії реалізації побудови нейро-фаззі моделей та гібридних моделей на основі інтеграції даних та знань;

вміти: проводити найбільш раціональний вибір функцій належності нечітких множин для формалізації лінгвістичних змінних та нечітких інтервалів; виконувати операції над нечіткими множинами; застосовувати алгоритми нечіткого логічного виведення Мамдані, ТСК та ін. для вирішення конкретних завдань; будувати нечіткі моделі, що використовуються для опису, аналізу та моделювання складних слабко формалізованих систем і процесів; оцінювати обчислювальну складність моделювання нечітких процесів.

Лабораторна робота №1 Нечіткі множини і операції над ними

1.1 Мета роботи

Метою заняття є вивчення основних понять теорії нечітких множин; вивчення методів побудови нечітких множин з використанням різних типів функцій приналежності; ознайомлення з найбільш поширеними логічними операціями над нечіткими множинами.

1.2. Методичні вказівки з організації самостійної роботи студентів

Основною причиною появи теорії нечітких множин (fuzzy sets) стали нечіткі і наближені міркування, що використовувались для опису людиною процесів, систем, об'єктів. Математична теорія нечітких множин (fuzzy sets) і нечітка логіка (fuzzy logic) є узагальненнями класичної теорії множин і класичної формальної логіки.

У класичній математиці під множиною розуміється сукупність елементів (об'єктів), що мають деяку спільну властивість. Наприклад, множина чисел, не менших заданого числа; множина векторів, сума компонентів кожного з яких не перевершує одиниці і т.п. При цьому, для будь-якого елемента множини розглядаються лише дві можливості: або цей елемент належить даній множині (тобто має дану властивість), або не належить даній множині (тобто не має даної властивості). Таким чином, в описі множини у звичайному розумінні необхідно дотримуватися чіткого критерію, що дозволяє судити про належність або неналежність будь-якого елемента даній множині.

Поняття нечіткої множини – спроба математичної формалізації нечіткої інформації з метою її використання при побудові математичних моделей складних систем. В основі цього поняття лежить уявлення про те, що елементи, які складають дану множину і мають деяку спільну властивість, можуть мати цю властивість в різному ступені і, отже, належати даній множини з "різним ступенем". При такому підході висловлення типу "елемент належить даній множині" втрачають зміст, оскільки необхідно вказати "наскільки сильно" або з яким ступенем даний елемент належить множині. Один з найпростіших способів математичного опису нечіткої множини – характеризація ступеня належності елемента множині чисел, наприклад, з інтервалу [0, 1]. Тобто нечітка множина є розширенням класичного канторівського поняття множини, з припущенням, що характеристична функція (функція належності елемента множині) може набувати будь-яких значень в інтервалі [0, 1], а не тільки значень 0 або 1. Також були визначені основні операції із нечіткими множинами.

Для підготовки до лабораторної роботи слід опрацювати конспект лекцій за темами: «Основні поняття теорії нечітких множин», «Операції над нечіткими множинами», а також відповідний матеріал з переліку рекомендованої літератури [1, 2, 3, 5, 6].

1.3. Методичні вказівки та короткі відомості щодо виконання лабораторної роботи

1. Виконати завдання 1, 2.

2. Оформити звіт за результатами лабораторної роботи та захистити його.

Завдання 1.

Задані і дві його нечітких підмножини і , де :

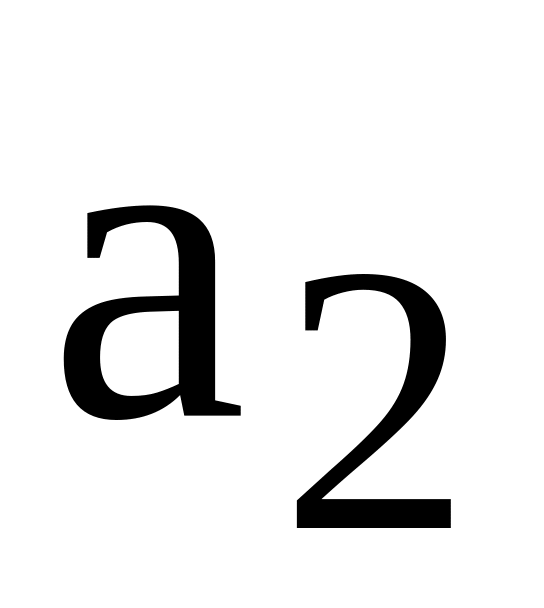
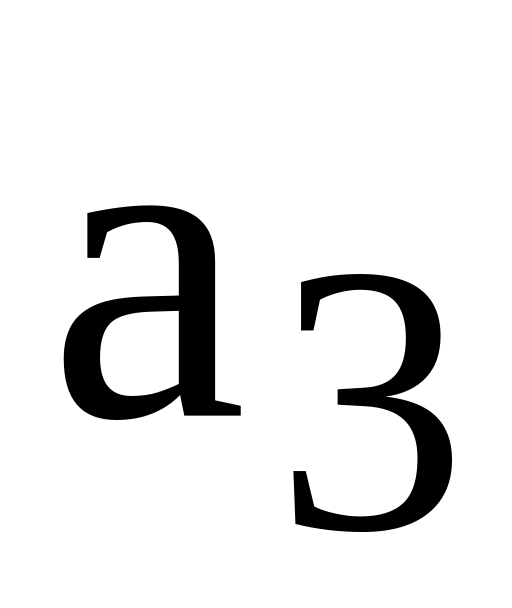
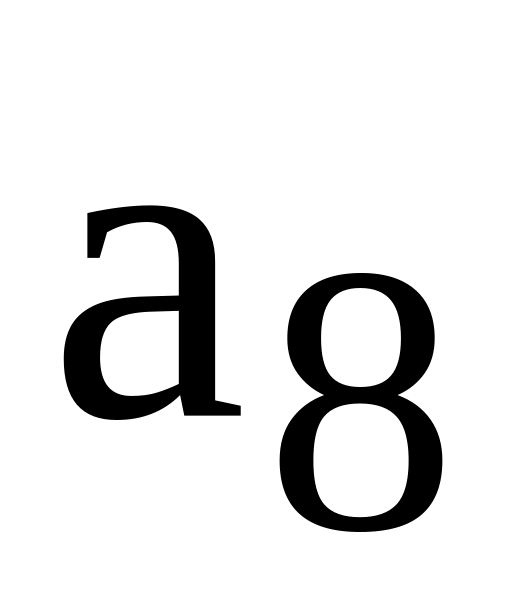
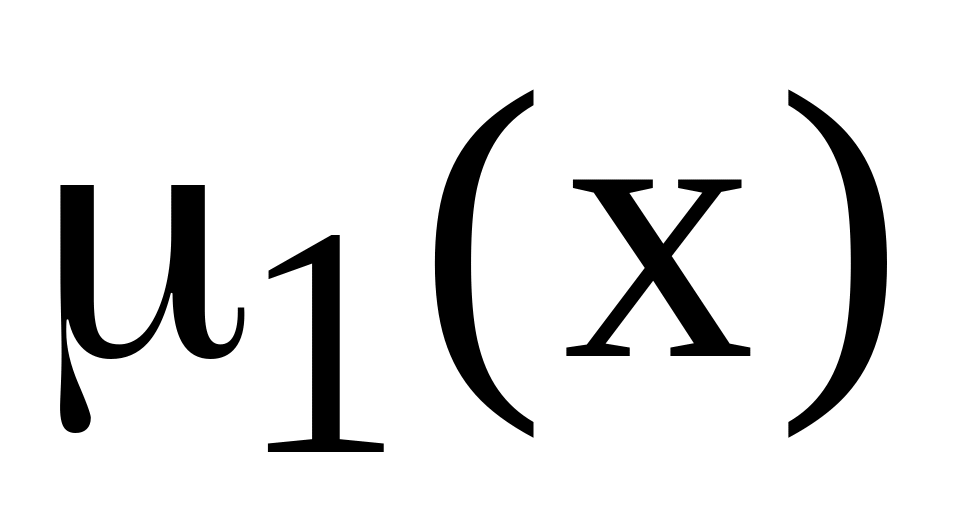
	0,1	0,6	0,9	1	0,5	0,8	0,4	0,5
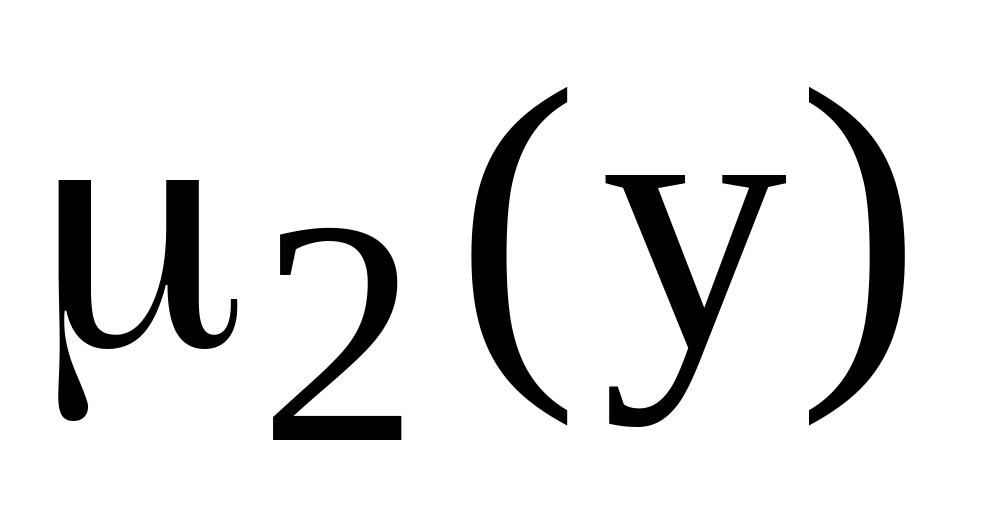
	0,7	0,5	1	0,6	0,4	0,3	0	0,2

Потрібно.

1. Представити Х і Y геометрично.

2. Знайти функції приналежності і представити геометрично множини: , , , , .

3. Знайти відстані між множинами Х і Y:

• абсолютну і відносну відстані Хеммінга;

• абсолютну і відносну відстані Евкліда.

4. Знайти підмножини (звичайні), найближчі до Х і Y. Обчислити індекси нечіткості Х і Y.

Варіанти завдань.

Варіант 1.

	0,2	0,8	0,5	1	0	0,9	0,3	0,4
	0,7	0	0	0,6	0,4	1	0	0,4

Варіант 2.

	1	0,6	0,3	0	0	0,5	0,5	0,9
	0,7	0,4	0	0,5	0,8	1	1	0,6

Варіант 3.

	0,5	0,3	0	0,8	0,9	1	0,4	0,2
	0,5	1	1	0,8	0,4	0	0	0,5

Варіант 4.

	0	0	0,7	0,6	0,1	0,5	0,8	1
	0,5	0,3	0	0,6	0,7	1	0,7	0,5

Варіант 5.

	0,4	0,7	0,2	0	0,3	0,7	1	0,7
	0,5	0,1	0	0,5	0,7	0,9	1	1

Варіант 6.

	1	1	0,6	0	0,7	0,4	0,1	0
	0,6	0,9	0,5	0,3	0	0,5	1	0.7

Варіант 7.

	0,5	0,8	1	0,4	0	0	0,2	0,6
	0,5	0,2	0,1	0	0	0,6	0,8	0,6

Варіант 8.

	1	0,5	0,6	0,9	0	0,5	0,4	0,2
	0	0,7	0,8	0,9	0,5	1	1	0

Варіант 9.

	0,6	0,4	0,8	0,5	0,9	0,3	0	0,2
	0,8	0,6	0,9	1	1	0,3	0	0

Варіант 10.

	0,4	0,5	0,2	0	0,5	0,7	0,9	1
	0,4	0,2	0,6	0,9	1	0,7	0,3	0,1

Розв’язання. Приведемо розв’язання задачі в електронній таблиці Excel (див. рис. 1–3).

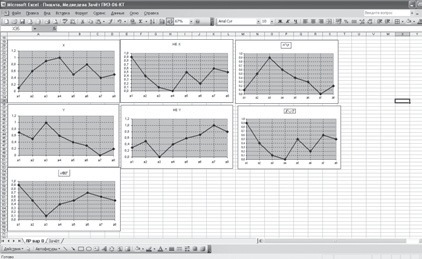
Рис. 1. Геометрична інтерпретація розв’язання завдання (п. 1, 2)

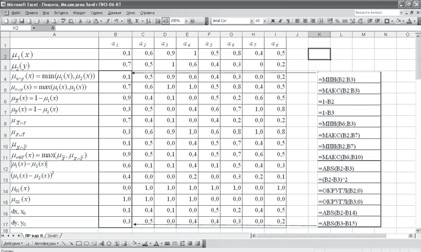
Рис. 2. Розв’язання завдання в Excel (п. 2)

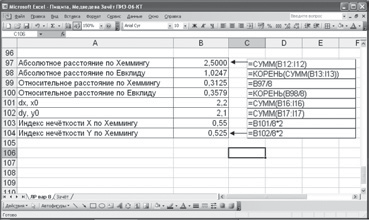
Рис. 3. Розв’язання завдання в Excel (п. 3, 4)

Вправа. Індекси нечіткості за евклідовою метрикою обчислить самостійно.

Завдання 2. Дослідити способи формування нечітких множин з використанням різних типів функцій приналежності і реалізувати операції над ними