Никитина Дарья ПИН-21Д ЛР2
.docx
Лабораторная
работа №2
Компьютерный
практикум по математическому анализу
никитина
дарья пин-21д



Текст программы
clear; clc;close all
% Практикум 2. Приложения определенного интеграла
% Упражнение 1 (Upr_2_1.m)
x=0:0.01:pi/2;
x1=0:0.1:10;
y=x.*cos(x);
y1=x1.*cos(x1);
subplot(2,1,1)
plot(x1,y1);grid
xlabel('x'); ylabel('y');
title('y=x*cos(x), 0 < x < 10pi')
subplot(2,1,2)
plot(x,y,'r',x,zeros(size(x)),'--r');grid
hold on
plot(x,x,'b--')
plot(x,-x,'g--')
ylim([-1,1])
hold off
xlabel('x'); ylabel('y')
title('y=x*cos(x), 0 < x < pi/2')
legend('y=xcos(x)','y=0','y=x','y=-x','Location','southeast')
syms x
I=int(x*cos(x), 0,pi/2);
fprintf('Интеграл =%5.4f\n ',double(I))
Результат
Интеграл =0.5708


Текст программы
clear; clc;close all
% Практикум 2. Приложения определенного интеграла
%1. Вычисление площадей фигур, ограниченных кривыми,
%заданными уравнениями в декартовых координатах.
% Упражнение (Upr_2_2.m)
% Определение координат х1 и х2 точек пересечения графиков
% Решение уравнения у2-у1=0 в символьном виде
syms x
sy=-2*x^2-6*x+7;% Символьная функция y2-y1
R=solve(sy,x);% Решение уравнения у2-у1=0
x1=double(R(1));% Левая граница интервала интегрирования
x2=double(R(2));% Правая граница интервала интегрирования
% Построение графиков, ограничивающих область интегрирования
x=x1:0.01:x2;
y1=x.^2+2*x;
y2=7-4*x-x.^2;
plot(x,y1,'r',x,y2,'b','LineWidth',2);grid
xlabel('x'); ylabel('y')
title('Область интегрирования')
legend('y1=x.^2+2*x','y2=7-4*x-x.^2')
I=double(int(sy,x1,x2));% Вычисление интеграла
% Вывод результата в окно команд
fprintf('Интеграл на отрезке [ %5.3f; %5.3f] равен %5.3f\n ',[x1 x2 I])
Результат
Интеграл на отрезке [ -3.898; 0.898] равен 36.768


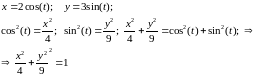
Получаем уравнение эллипса с полуосями a=2; b=3
Текст программы
clear; clc;close all
% Практикум 2. Приложения определенного интеграла
%2. Вычисление площади фигуры, ограниченной кривой,
% заданной параметрически
% 2. Вычисление площади фигуры, ограниченной кривой, заданной параметрически
% Упражнение 3. (Upr_2_3.m)
% Случай а).
t=0:0.01:2*pi;
disp('а).Площадь ограниченная линиями x=cos(t)^n; y=sin(t).^n;')
n=input(' Введите n = ');
x=cos(t).^n; y=sin(t).^n;
dx=-n*cos(t).^(n-1).*sin(t);%Производная x'(t)
plot(x,y,'r','LineWidth',1.5);grid
xlabel('x'); ylabel('y')
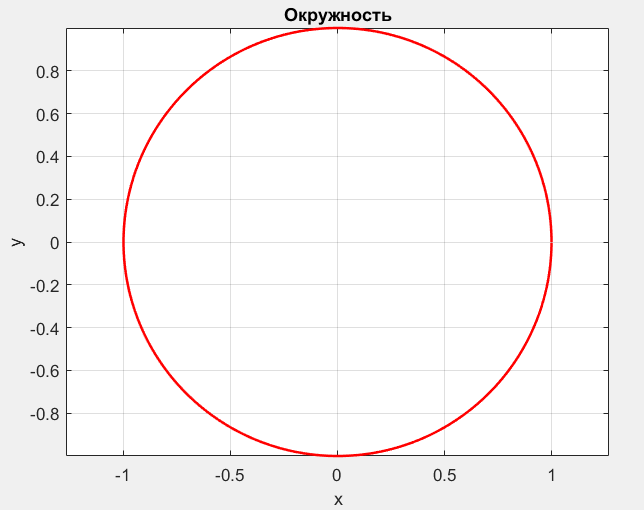
if n==1
Tit='Окружность';
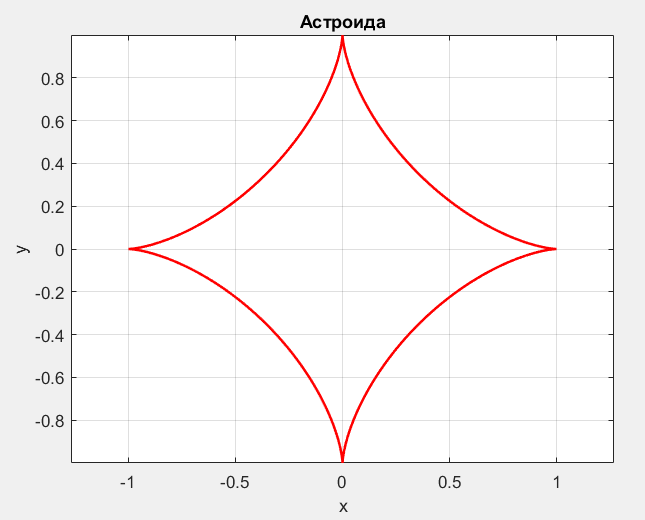
else
Tit='Астроида';
end
title(Tit)
axis equal
syms t
sf=sin(t).^n.*(-n*cos(t).^(n-1).*sin(t));% Подынтегральная функция
Is=int(sf,2*pi,0);% Интеграл
disp('Интеграл в символьном виде')
disp(Is)
I=double(Is);
fprintf('Численное значение площади = %5.3f\n ',I)
% Случай b)
disp(' ')
disp('б). Площадь ограниченная линиями x=2cos(t); y=3sin(t)')
t=0:0.01:2*pi;
x1=2*cos(t); y1=3*sin(t);
figure
plot(x1,y1,'r','LineWidth',1.5);grid
axis equal
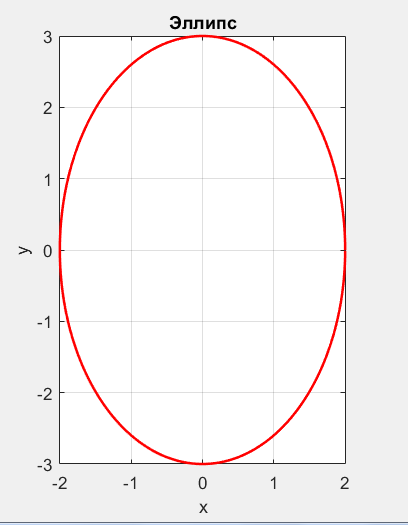
% Эллипс с полуосями a=2 и b=3 помещен в рамку графической области
axis([-2, 2, -3 ,3]);
xlabel('x'); ylabel('y')
title('Эллипс')
syms t
sf1=3*sin(t).*(-2*sin(t));% Подынтегральная функция
Is1=int(sf1,2*pi,0);% Интеграл
disp('Интеграл в символьном виде')
I1=double(Is1);
disp(Is1)
I1=double(Is1);
fprintf('Численное значение площади = %5.3f\n ',I1)
Результат
а).Площадь ограниченная линиями x=cos(t)^n; y=sin(t).^n;
Введите n = 1
Интеграл в символьном виде
pi
Численное значение площади = 3.142
а).Площадь ограниченная линиями x=cos(t)^n; y=sin(t).^n;
Введите n = 3
Интеграл в символьном виде
(3*pi)/8
Численное значение площади = 1.178
б). Площадь ограниченная линиями x=2cos(t); y=3sin(t)
Интеграл в символьном виде
6*pi
Численное значение площади = 18.850

Текст программы
clear; clc;close all
% Практикум 2. Приложения определенного интеграла
%3. Вычисление площади фигуры, ограниченной кривой,
%заданной уравнением в полярных координатах.
% Упражнение 4. (Upr_2_4.m)
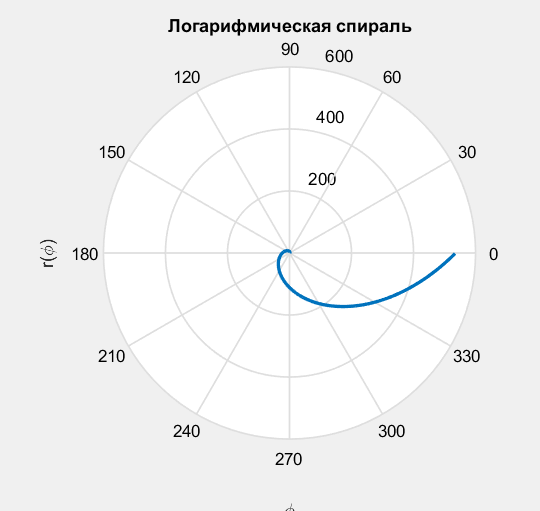
%% ==== Случай а). ==========
fi=0:0.01:2*pi;
r=exp(fi);
p=polar(fi,r);
xlabel('\phi'); ylabel('r(\phi)')
title('Логарифмическая спираль')
set(p,'LineWidth',2)
% Вычисление площади
syms fi
Is=int(exp(2*fi),0,2*pi)/2;
disp('Интеграл в символьном виде')
disp(Is)
I=double(Is);
fprintf('Численное значение площади, ограниченной спиралью = %5.3f\n ',I)
%% ======== Случай б),================
figure
% Построение дуг
fi=pi/4:0.01:3*pi/4;
r1=1; r2=2;
p=polar(fi,r2*ones(size(fi)));
set(p,'LineWidth',2)
hold on
p1=polar(fi,r1*ones(size(fi)));
set(p1,'LineWidth',2)
% Построение лучей
rr=1:0.1:2;
p2=polar(pi/4*ones(size(rr)),rr);
set(p2,'LineWidth',2)
p3=polar(3*pi/4*ones(size(rr)),rr);
set(p3,'LineWidth',2)
xlabel('\phi'); ylabel('r(\phi)')
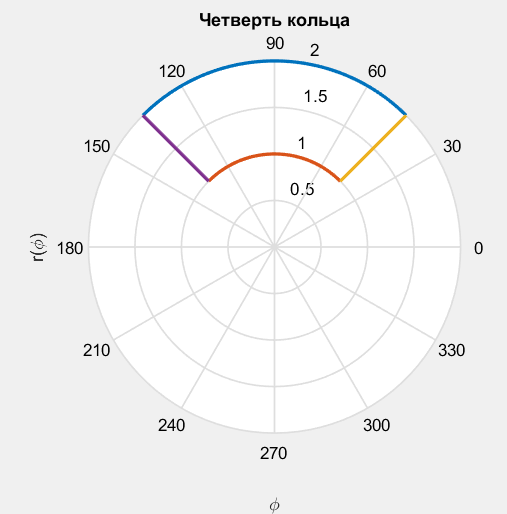
title('Четверть кольца')
hold off
% Вычисление площади 1/4 кольца
S=(pi*r2^2-pi*r1^2)/4;
disp(' ')
fprintf('Значение площади четверти кольца = %5.3f\n ',S)
Результат
Интеграл в символьном виде
exp(4*pi)/4 - 1/4
Численное значение площади, ограниченной спиралью = 71687.578
Значение площади четверти кольца = 2.356

Текст программы
clear; clc;close all
% Практикум 2. Приложения определенного интеграла
% 4. Вычисление длины дуги. Декартортовая система координат
% Упражнение 5. (Upr_2_5.m)
x=1:0.1:2;
y=x.^2;
plot(x,y','r','LineWidth',2);grid
xlabel('x'); ylabel('y')
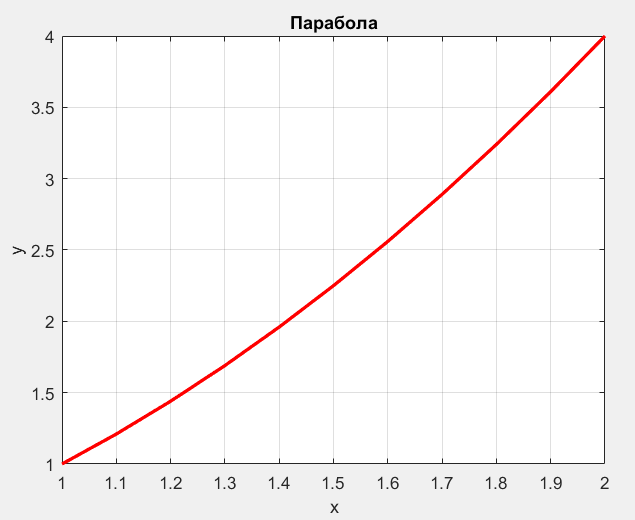
title('Парабола')
dy=2*x;
syms x
Is=int(sqrt(1+(2*x)^2),1,2);
disp('Интеграл в символьном виде:')
disp(Is)
I=double(Is);
fprintf('Численное значение длины дуги параболы = %5.3f\n ',I)
Результат
Интеграл в символьном виде:
log(17^(1/2) + 4)/4 - log(5^(1/2) + 2)/4 - 5^(1/2)/2 + 17^(1/2)
Численное значение длины дуги параболы = 3.168

Текст программы
clear; clc;close all
% Практикум 2. Приложения определенного интеграла
% 4. Вычисление длины дуги параметрически заданной
% Упражнение 6 (Upr_2_6.m)
t=0:0.01:2*pi;
x=cos(t).^3;
y=sin(t).^3;
plot(x,y','r','LineWidth',2);grid
xlabel('x'); ylabel('y')
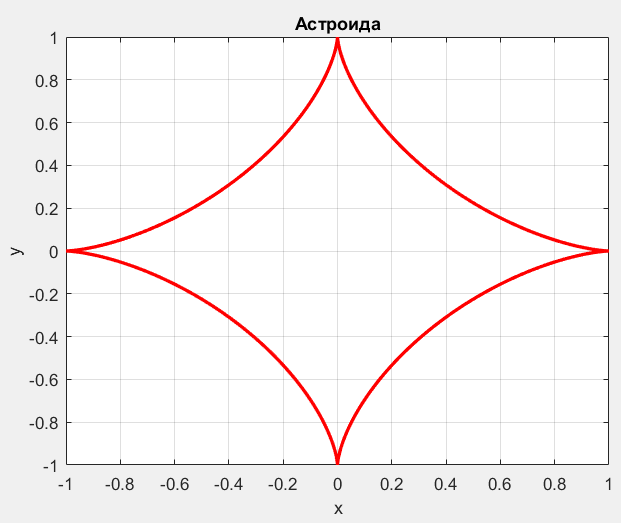
title('Астроида')
syms t
fs=sqrt(cos(t).^6+sin(t).^6);% Подынтегральная функция
Is=int(fs,0,2*pi);
I=double(Is);
fprintf('Длины дуги астроиды = %5.3f\n',I)
Результат
Длины дуги астроиды = 4.844
Текст программы
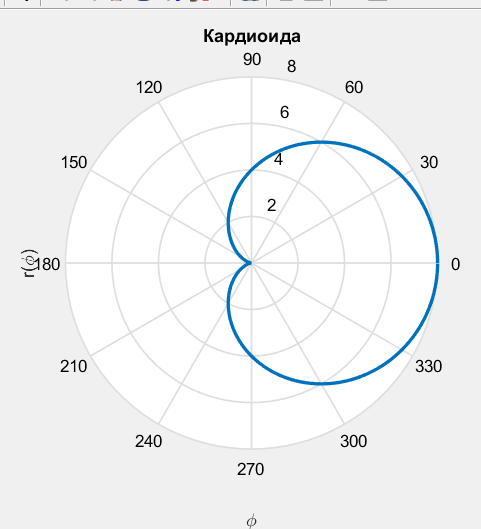
% 4. Вычисление длины дуги заданной в полярных координатах
% Упражнение 7 (Upr_2_7.m)
fi=0:0.01:2*pi;
r=4*(1+cos(fi));
p=polar(fi,r);
set(p,'LineWidth',2)
xlabel('\phi'); ylabel('r(\phi)')
title('Кардиоида')
syms fi
fs=sqrt(16*(1+cos(fi)).^2+(-4*sin(fi)).^2);% Подынтегральная функция
% Вычисление длины дуги
Is=int(fs,0,2*pi);
I=double(Is);
fprintf('Длина дуги кардиоиды = %5.3f\n',I)
Результат
Длина дуги кардиоиды = 32.000

Текст программы
clear; clc;close all
% Практикум 2. Приложения определенного интеграла
% 5. Вычисление объема тела вращения.
% Упражнение 8 (Upr_2_8.m)
%% ==== Вычисление объема тела вращения вокруг оси Ох =======
% Построение графика синусоиды
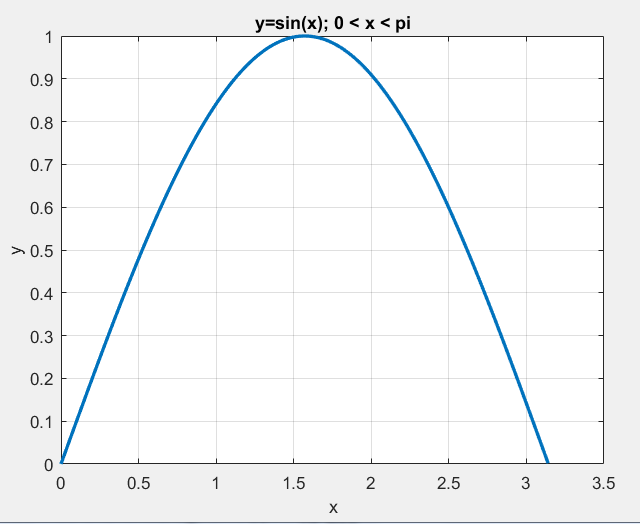
x=0:0.01:pi;
y=sin(x);
plot(x,y,'LineWidth',2);grid
xlabel('x'); ylabel('y');
title('y=sin(x); 0 < x < pi')
%Вычисление определенного интеграла в символьном виде
disp('Объем тела вращения вокруг оси Ох')
syms x
fsx=sin(x).^2;% Подынтегральная функция
Isx=pi*int(fsx,0,pi);%Вычисление определенного интеграла
disp('Объем в символьном виде:')
disp(Isx)
Vx=double(Isx);
fprintf('Численное значения объема Vx = %5.3f\n ',Vx)
%% ==== Вычисление объема тела вращения вокруг оси Оу =======
disp(' ')
disp('Объем тела вращения вокруг оси Оy')
fs=x.*sin(x);% Подынтегральная функция
Isy=2*pi*int(fs,0,pi); %Вычисление определенного интеграла
disp('Объем в символьном виде:')
disp(Isy)
Vy=double(Isy);
fprintf('Численное значения объема Vy = %5.3f\n ',Vy)
%% ======== Построение поверхностей тел вращения ===
u = linspace(0, pi, 30);
v = linspace(0, pi, 30);
x=0:0.1:pi;
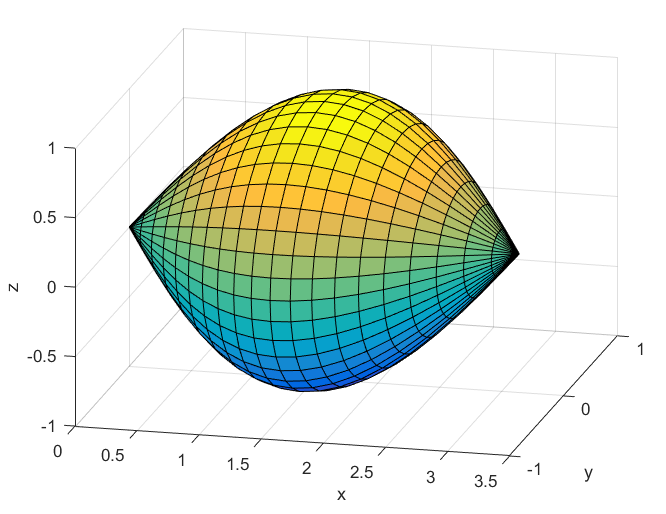
% Вращение функции y=sin(x) вокруг оси Ох
u = (0:0.05*pi:pi)';
v = [0:0.05*pi:2*pi];
X = u*ones(size(v));
Y = sin(u)*cos(v);
Z = sin(u)*sin(v);
figure('Color','w')
surf(X,Y,Z);
xlabel('x'); ylabel('y'); zlabel('z')
view(14,24)
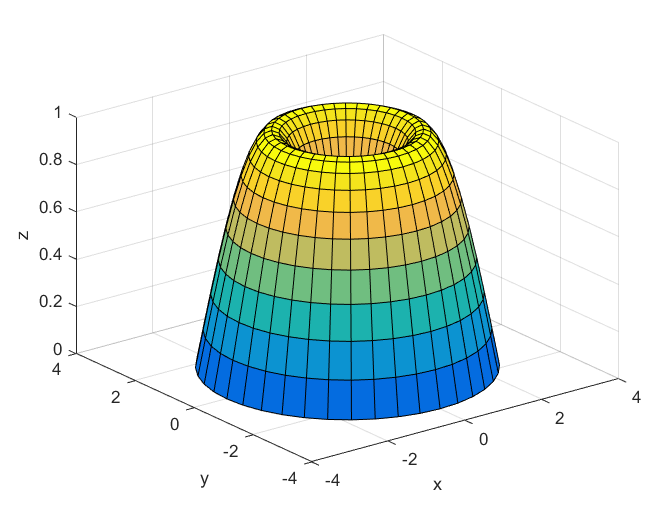
% Вращение функции y=sin(x) вокруг оси Оу
u = (0:0.05*pi:pi)';
v = [0:0.05*pi:2*pi];
X = u*sin(v);
Y = u*cos(v);
Z = sin(u)*ones(size(v));
figure('Color','w')
surf(X,Y,Z);
xlabel('x'); ylabel('y'); zlabel('z')
Результат
Объем тела вращения вокруг оси Ох
Объем в символьном виде:
pi^2/2
Численное значения объема Vx = 4.935
Объем тела вращения вокруг оси Оy
Объем в символьном виде:
2*pi^2
Численное значения объема Vy = 19.739