
Контрольная
работа №2
КОМПЬЮТЕРНЫЙ
ПРАКТИКУМ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
НИКИТИНА
ДАРЬЯ ПИН-21Д


Вариант 2
1.
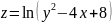 .
.
а) Изобразить в MATLAB график функции,
б) изобразить в MATLAB область определения
Линии, не принадлежащие области определения, выделять пунктиром!!!
2.
Изобразить
на координатной плоскости линии уровня
для функции
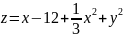 ,
придавая
,
придавая
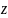 значения от
значения от
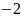 до
до
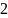 через 1.
через 1.
а) Построить в MATLAB линии уровня непосредственно по заданию. б) построить поверхность, состоящую из линий уровня при помощи функции с шагом 0,1. в) построить плоские линии уровня без нанесения и с нанесением значений функции с шагом 0,5. Нанести сетку.
3. Записать уравнения касательной плоскости и нормали к поверхности S в точке M0
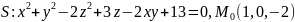 .
.
а) Изобразить в MATLAB поверхность, б) изобразить в MATLAB на одном рисунке поверхность локально около точки M0 , касательную плоскость и нормаль. Выбрать несколько ракурсов рисунка
4.
Найдите точное (
 ) и приближенные (
) и приближенные ( )
, (
)
, (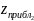 )
значения функции
)
значения функции
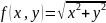 в
точке (4,05; 2,96)
в
точке (4,05; 2,96)
найти, используя полный дифференциал функции двух переменных; - используя формулу Тейлора до 2-го порядка включительно
а)
в MATLAB
на одном рисунке построить локально
около исследуемой точки
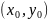 поверхность
поверхность
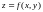 и поверхность
и поверхность
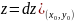 .
Провести через т
вертикальную линию параллельно оси
аппликат OZ.
Отметить точное значение функции
на поверхности
и приближенное значение на поверхности
.
Показать разность (выделить
жирный отрезок
на прямой)
приращения аппликаты
.
Провести через т
вертикальную линию параллельно оси
аппликат OZ.
Отметить точное значение функции
на поверхности
и приближенное значение на поверхности
.
Показать разность (выделить
жирный отрезок
на прямой)
приращения аппликаты
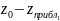 .
.
б)
На втором рисунке тоже самое проделать
с поверхностью
и функцией
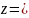 Провести вертикальную линию
параллельно оси аппликат OZ.
Отметить точное значение функции
на поверхности
и приближенное значение на поверхности
.
Показать разность (выделить
жирный отрезок
на прямой)
приращения аппликаты
Провести вертикальную линию
параллельно оси аппликат OZ.
Отметить точное значение функции
на поверхности
и приближенное значение на поверхности
.
Показать разность (выделить
жирный отрезок
на прямой)
приращения аппликаты
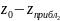 .
.
5. Найти точки безусловного экстремума (добавить исследование в письменную часть). а) В MATLAB построить поверхность , по возможности, определить визуально наличие и примерное расположение точек безусловного минимума и максимума функции . Отметить точки на рисунках в матлаб, сравнить с письменным исследованием.
б)
В MATLAB
построить
на поверхности
кривую,
определяемую ограничением
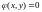 .
По возможности, определить визуально
наличие и примерное расположение точек
условного
минимума и максимума
этой функции при данном ограничении.
.
По возможности, определить визуально
наличие и примерное расположение точек
условного
минимума и максимума
этой функции при данном ограничении.
в,г,д)
Изобразить эту же кривую без самой
поверхности в пространстве и в различных
ракурсах (в
плоскости OZX,
OZY),
отметить на рисунке точки условного
экстремума.
Найти точки экстремума
функции
 при условии, что
при условии, что
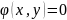 (использовать прямой метод)
(использовать прямой метод)
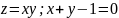 .
.
Результаты, полученные в MATLAB, должны снабжаться краткими пояснениями. На рисунках экономить ненужно. Бывает не лишним сделать рисунки в различных приближениях и ракурсах.
Вариант 2
1. .
а) Изобразить в MATLAB график функции,
б) изобразить в MATLAB область определения
Линии, не принадлежащие области определения, выделять пунктиром!!!
Решение:
ООФ:
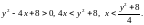

Область определения функции (темно синяя область), граница (парабола) не входит.
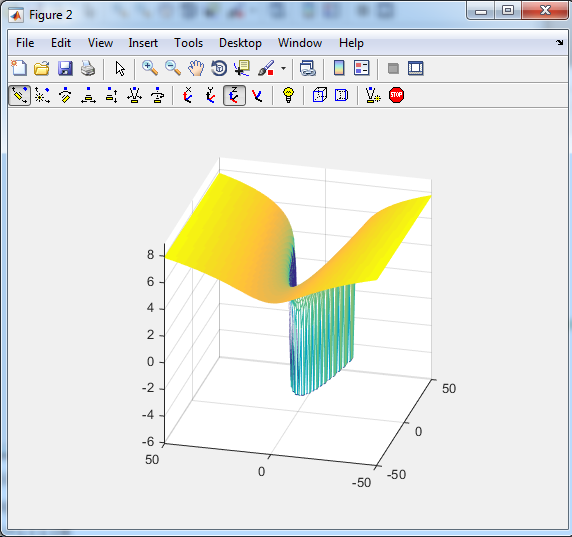
При
подходе точки к границе (парабола)
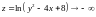 ,
поэтому, для наглядности, поверхность
обрезали снизу плоскостью
,
поэтому, для наглядности, поверхность
обрезали снизу плоскостью
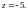
clc;
Minx=-10;%нижняя граница оси X
Maxx=100;%верхняя граница оси X
Miny=-20;%нижняя граница оси Y
Maxy=20;%верхняя граница оси Y
x=Minx:0.1:Maxx;% сетка по оси X
X=[Minx Maxx];
Y=[Miny Maxy];
Z=[0 0];% линия координат
hold on
x=-2:0.1:100;%сетка по оси OX
y=2*sqrt(x+2);% верхняя полупарабола
y1=-2*sqrt(x+2);% нижняя полупарабола
figure(1);
hold on;
X1=[-20 100 100 -20 -20];
Y1=[-25 -25 25 25 -25];
fill(X1,Y1,[0 0 1]);% закрашивание прямоугольника
fill([x fliplr(x)], [y fliplr(y1)], [1 1 1])% закрашивание внутренности параболы
plot(x,y,'g:',x,y1,'g:');% график параболы
plot(X,Z, 'k');% ось X
plot(Z,Y, 'k');% ось Y
x=-50:1:50;%сетка по оси OX
y=-50:1:50;
y1=-50:1:50;
N=length(x);
for i=1:1:N
for j=1:1:N
a(i,j)=y(i)^2-x(j)*4+8;
a1(i,j)=y1(i)^2-x(j)*4+8;
if a(i,j)<=0.001
z(i,j)=-5;% обрезка нижней части поверхности
else
z(i,j)=log(a(i,j));
end
if a1(i,j)<=0.001
z1(i,j)=-5;% обрезка нижней части поверхности
else
z1(i,j)=log(a(i,j));%формирование 3-й координаты поверхности
end
end
end
figure(2);
mesh(x,y,z);% одна половина (y>0)поверхности
hold on;
mesh(x,y1,z1);% другая половина (y<0)поверхности
