
- •Теоретические основы электротехники
- •Применение функций комплексного переменного для описания плоскопараллельных полей
- •Функция потока
- •Выражение для напряженности через функцию потока
- •Уравнения Лапласа для функций потенциала и потока
- •Функция комплексного переменного
- •Сравнение условий Коши-Римана и выражений для напряженности поля:
- •Метод заданного комплексного потенциала.
- •. Пусть комплексный потенциал задан в виде:
- •Поле уединенного заряженного кругового цилиндра
- •. Поле двух тонких заряженных нитей
- •Линии равного потенциала в системе двух заряженных проводов
- •Линии равной напряженности поля в системе двух заряженных проводов
- •Картина поля двух линейных проводов и реальной линии передачи
- •Поле параллельных несоосных цилиндров
. Пусть комплексный потенциал задан в виде:
W(z) = jA ln z = jA ln(r·ej ) = jA ( ln r + j ) = – A + jA ln r = V + jU,
тогда:
V = – A = const уравнение линии напряженности, т.е. = const. Эти линии представляют собой лучи, исходящие из начала координат;
U = A ln r = const уравнение линии равного потенциала, т.е. r = const . Эти линии представляют собой концентрические окружности с центром в начале координат.
Принимая постоянным приращения потенциала и функции потока ( V = const и
U = const), получаем постоянство приращения координаты = const при переходе от одной к другой линии напряженности и постоянство отношений
радиусов соседних линий равного потенциала |
|
|
rk 1 |
const |
|
|
rk |
||||||
|
|
|
|
|
||
|
|
|
|
|
|

Поле уединенного заряженного кругового цилиндра
При =2 получаем поверхность, охватывающую весь проводник с полным зарядом
V3
V4
U3 |
V |
|
2 |
|
U2 |
 U1 V1
U1 V1
U1 U2 U3 |
V1 V2 V3 |
E q |
|
V |
q |
|
|
|
|
l |
|
||||
|
|
|
|
|||
V A 2 |
|
|
A |
|
|
|
|
|
2 |
||||
|
|
|||||
|
|
|
|
|||
V |
|
|
U |
|
ln r |
|
2 |
2 |
|||||
|
|
|
|

Поле создается тонкой заряженной нитью, расположенной в точке с координатой z = z0
W(z) = jA ln z |
|
|
|
|
|
|
|
|
|
|
W = j A ln( z – z0) |
|
||
j y |
|
|
||
|
|
|
||
|
E |
|||
|
|
|
||
z |
|
z – z0 |
x |
|
0  z0
z0
. Поле двух тонких заряженных нитей
Для двух заряженных нитей с зарядами 1 и 2, расположенных в точках с координатами z10 и z20 запишем выражение для комплексного потенциала, воспользовавшись принципом наложения:
W (z) = jA1 ln (z–z10) + jA2 ln (z–z20) + C1 + j
|
|
|
C2. |
|
||
C1 и C2 – произвольные постоянные, зависящие от выбора места расположения начальных (нулевых) |
||||||
линий функции потока и потенциал |
|
|
|
|||
A1 |
1 |
A2 |
|
2 |
1 = – 2 = |
|
2 |
2 |
|||||
|
|
|
||||
Комплексный потенциал в произвольной точке имеет вид:
W j |
|
ln |
z z10 |
C1 jC2 |
|
2 |
z z20 |
||||
|
|
|

W |
j |
|
ln |
z z10 |
2 |
z z20 |
z1
– b
W
C1 jC2 |
z10 = – b ; z20 = |
|
+ b |
y
|
|
|
r1 |
r2 |
|
= (z + b) |
z |
z2 = (z – b) |
|
||
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
0 |
|
+ b |
x |
j |
|
ln z b |
C1 jC2 |
|
|
|
2 |
z b |
|
|
|
z1 = z + b = r1 e j 1 |
|
|
|
z2 = z – b = r2 e j 2 |
|
|
|
|
|
|
|
|||||||||||
W j |
|
|
|
ln |
|
z b |
C1 |
jC2 |
W j |
|
ln |
r1 |
e |
j( 1 |
2 ) |
C1 |
jC2 |
|||||
|
|
|
|
|
|
|
2 |
r2 |
|
|
||||||||||||
|
2 |
|
z b |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
W j |
|
|
|
ln |
r2 |
|
jC2 |
|
|
( 1 2 ) C1 = V + j U |
|
|
|
|
|
|
|
|
||||
|
|
|
|
r1 |
2 |
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Положим C2=0 , тогда получим U=0 при r1=r2, то есть линия нулевого потенциала – это ось ординат
U |
|
|
ln |
r2 |
C2 |
V |
|
|
( 2 1 ) C1 |
||
|
2 |
||||||||||
2 |
r1 |
||||||||||
|
|
|
|
|
|
||||||
U |
|
|
ln r2 |
C2 const |
|
r2 |
const |
||||
2 |
|
r |
|||||||||
|
|
r1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
|
|

Линии равного потенциала в системе двух заряженных проводов
Линии равного потенциала – это окружности с центрами на оси OX с координатами центра:
r |
k const |
|
|
|
x0 |
|
|
|
1 k 2 |
b |
y0 0 |
||
2 |
|
|
|
|
k |
2 |
|||||||
r1 |
|
|
|
||||||||||
|
|
|
|
|
|
1 |
|
|
|
||||
и радиусом: |
R |
|
|
2k |
|
|
|
b |
|
|
|
|
|
|
|
1 k 2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Чтобы приращение потенциала при переходе от любой линии равного потенциала к соседней оставалась постоянным, должно быть соблюдено условие:
|
|
|
r2, 1 |
|
r2, |
|
|
|
|
k 1 |
|
k 1 |
|
|
U U 1 U |
ln |
ln |
|
|
ln |
const |
B const |
|||||||
|
|
|
||||||||||||
|
r |
|
2 |
k |
||||||||||
|
2 |
|
r |
|
|
|
k |
|||||||
|
|
|
1, 1 |
|
1, |
|
|
|
|
|
|
|
||

Линии равной напряженности поля в системе двух заряженных проводов
Положив в выражении для функции потока C1=0, получим V=0 при 2 |
1 |
||||||||
V |
|
( |
|
) const |
|
2 |
|
const |
|
|
2 |
|
|||||||
|
2 |
|
1 |
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
Линия напряженности поля является уравнением дуги окружности, пересекающейся с проводами
КоординатыV V 1 V центров окружностей:
|
0 |
y bctg |
x0 |
0 |
|
|
bctg( ) bctg |
|
y0 |
||
V V 1 V |
const |

Картина поля двух линейных проводов и реальной линии передачи
B 3
/ 6
Формулы для определения положения линейных проводов (электрических осей) , эквивалентным двум проводам круглого сечения
h x0 - координата центра окружности равного потенциала
h |
|
1 k 2 |
|
|
b |
R |
|
|
2k |
|
|
|
b |
|||
|
|
|
|
|
1 k |
2 |
|
|
||||||||
|
|
|
|
|
||||||||||||
|
|
1 |
k |
2 |
|
|
|
|||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b h2 R2
На рисунке заштрихованы сечения проводов около контуров сечений
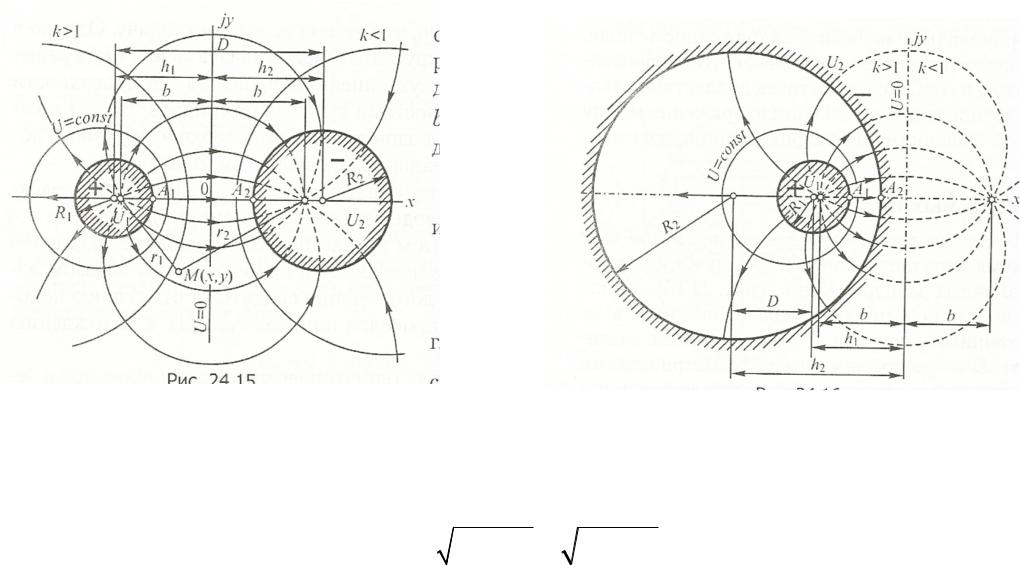
Поле параллельных несоосных цилиндров
|
|
|
|
|
Положение плоскости нулевого потенциала: |
|
|
D2 |
R22 R12 |
||||||||
|
D |
2 |
2 |
2 |
|
D |
2 |
2 |
2 |
h1 |
|
D2 |
R12 R22 |
h2 |
|
||
h1 |
|
R1 |
R2 |
h2 |
|
R1 |
R2 |
|
2D |
|
2D |
||||||
|
|
2D |
|
|
|
2D |
|
|
|
|
|
|
|
||||
b h2 |
R2 |
|
h2 |
R2 |
- положение электрических осей |
1 |
1 |
|
2 |
2 |
|
