- •Сложный теплообмен (теплопередача)
- •Расчетная формула стационарного процесса теплопередачи имеет следующий вид:
- •Однако, во многих случаях можно рассматривать величину коэффициента теплопередачи постоянной по всей поверхности
- •Теплопередача чрез плоскую стенку
- •На основе закона Фурье и уравнения Ньютона – Рихмана можно написать:
- •Решая эти уравнения относительно разности температур, находим:
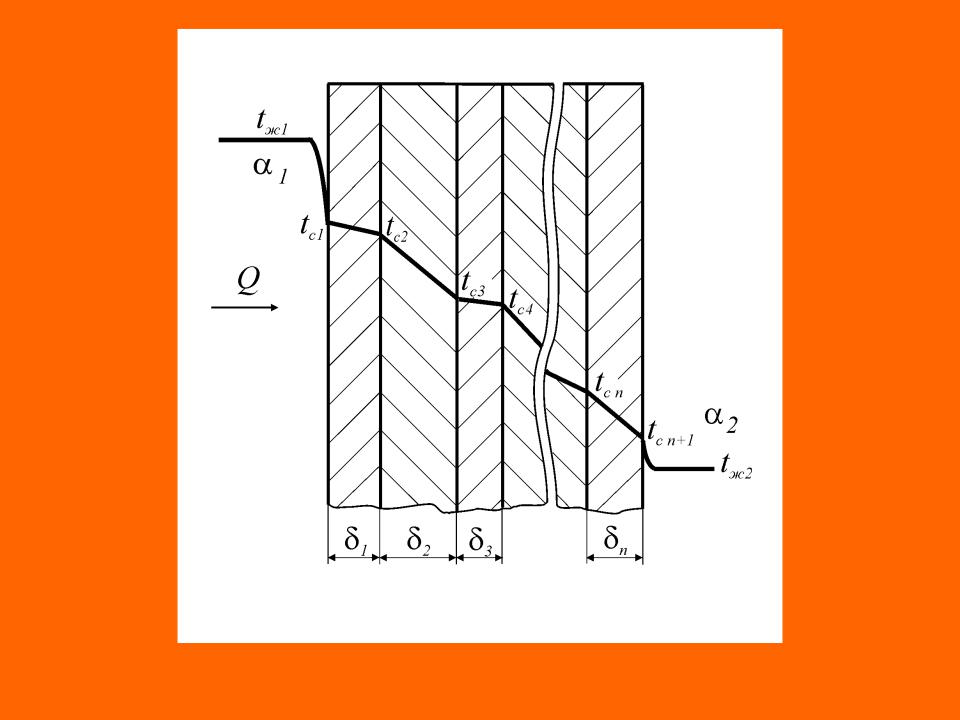
- •В случае теплопередачи через многослойную стенку, состоящую из n слоев тепловой поток и
- •Теплопередача через цилиндрическую стенку
- •Тепловой поток, передаваемый от горячего теплоносителя к поверхности стенки
- •Решая уравнения относительно разности температур и суммируя полученные выражения, получим расчетное уравнение для
- •После определения величины теплового потока Q можно найти температуры на поверхности стенки:
- •Уравнение теплопередачи для криволинейной поверхности
- •где Fmi – средняя поверхность теплопередачи, в частном
- •Линейное термическое сопротивление стенки
- •Увеличение ∆t может быть связано с изменением технологии процесса, что не всегда возможно.

Сложный теплообмен (теплопередача)
Процесс передачи теплоты от одной среды (теплоносителя) к другой среде (теплоносителю) через разделяющую их стенку называется теплопередачей и состоит из процессов теплоотдачи от горячего теплоносителя к поверхности стенки, передачи теплоты теплопроводностью через многослойную (или однослойную) стенку и процесса теплоотдачи от поверхности стенки к холодному теплоносителю. При установившемся процессе теплопередачи средние температуры горячего и холодного теплоносителей (сред) остаются постоянными вдоль поверхности стенки, а тепловой поток сохраняет неизменное значение (Q = const).

Расчетная формула стационарного процесса теплопередачи имеет следующий вид:
Q kF tср
где Q – тепловой поток; k – коэффициент теплопередачи; F – площадь поверхность теплопередачи; tср = (tm1 – tm2) – средний
температурный напор (средняя разность температур).
Коэффициент теплопередачи k выражает количество передаваемой теплоты в единицу времени через единицу площади поверхности при температурном напоре равном 1 градусу.
В большинстве случаев при движении теплообменивающи- хся жидкостей вдоль поверхности теплообмена их температуры изменяются. Коэффициент теплопередачи также изменяется по поверхности теплообмена.

Однако, во многих случаях можно рассматривать величину коэффициента теплопередачи постоянной по всей поверхности теплообмена, а разность температур между жидкостями принимать средней по поверхности теплообмена.
В этом случае для определения теплового потока имеем
Q k tdF
Коэффициент теплопередачиF имеет очень важное прикладное
значение. Расчетные формулы для определения коэффициента теплопередачи, а также формулы для определения среднего температурного напора (средней разности температур) рассматриваются ниже.

Теплопередача чрез плоскую стенку
Рассмотрим процесс передачи теплоты через плоскую стенку с площадью поверхности F, толщиной стенки , коэффициентом теплопроводности материала стенки , при известных температурах горячего tж1 и холодного
теплоносителей, а также коэффициентов теплоотдачи от горячего 1 и холодного 2 теплоносителей. Температура
на внешних поверхностях стенки неизвестны.
При стационарном температурном поле системы тепловой поток и плотность теплового потока постоянны.
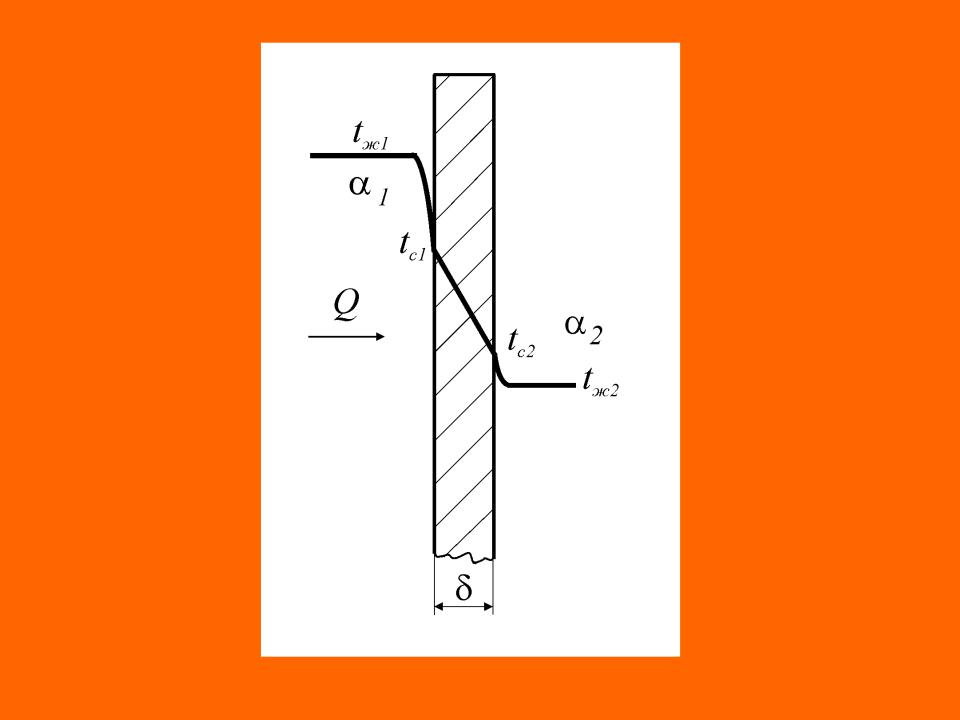

На основе закона Фурье и уравнения Ньютона – Рихмана можно написать:
плотность теплового потока, передаваемого от горячего теплоносителя поверхности стенки
q1 QF 1 tж1 tс1
та же плотность теплового потока передается теплопроводно-
стью через стенку
q2 QF tc1 tc2
и передается от поверхности стенки к холодному
теплоносителю
q3 QF 2 tж2 tс2

Решая эти уравнения относительно разности температур, находим:
tж1 tc1 1 q1 R1q1 ;
1
tc1 tc2 1 q2 R2q2 ;
1
tc2 tж2 1 q3 R3q3 .
2
Складывая по частям выражения разностей температур и учитывая, что q q1 q2 q3 получим выражение для
итоговой разности температур
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|
t |
|
t |
|
|
|
|
|
|
|
|
q R |
R |
R q Rq, |
ж1 |
ж2 |
|
|
|
|
|
|
|
|||||
|
|
|
|||||||||||
|
|
|
1 |
|
1 |
|
|
1 |
2 |
3 |
|||
|
|
|
|
|
|
|
2 |
|
|
|
|||

где R R1 R2 R3 |
– термическое сопротивление |
теплопередачи |
плоской стенки (м2К\Bm); |
R |
1 |
; |
R2 |
|
; |
R3 |
1 |
|
|
|
|||||
|
|
||||||
1 |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
– термические сопротивления теплоотдачи со стороны горячего теплоносителя, теплопроводности плоской стенки и термические сопротивления теплоотдачи со стороны холодного теплоносителя соответственно.
Отсюда, следует выражение для плотности теплового потока |
|||
и теплового потока (уравнение теплопередачи плоской |
|||
стенки): |
q |
1 |
tж1 tж2 k tж1 tж2 ; |
|
R |
||
|
|
|
|
Q qF kF tж1 tж2

где k=1/R – коэффициентом теплопередачи плоской стенки,
Вт/(м2 ∙К)
1 |
1 |
|
|
|
|
1 |
|
|
|
|
||
k |
|
|
|
|
|
|
|
|
|
|
, |
|
R |
R1 R2 R3 |
|
1 |
|
|
|
1 |
|
||||
|
|
|
|
2 |
||||||||
|
|
|
|
|
|
1 |
|
|
||||
После определения количества передаваемой теплоты (Q, q) можно найти температуры на поверхностях стенки из выражений разности температур:
t t |
|
q 1 t |
q 1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
с1 |
ж1 |
|
|
|
ж2 |
|
|
|
|
|
1 |
2 |
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
tс2 |
tж2 |
q |
|
tж1 |
q |
|
|
|
|
2 |
1 |
|
|||||||
|
|
|
|
|
|
|
|||

В случае теплопередачи через многослойную стенку, состоящую из n слоев тепловой поток и плотность теплового потока и следовательно коэффициент теплопередачи определяются с учетом термических сопротивлений каждого слоя
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
k |
|
|
|
|
|
|
|
||||||||||
R |
R R R |
|
|||||||||||||||
|
|
|
|
|
|
1 |
|
2 |
|
|
3 |
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
|
i n |
|
|
i |
|
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Температура поверхности и на стыке |
слоев определяется из тех же |
||||||||||||||||
|
|
1 |
|
|
i 1 |
|
|
|
i |
|
|
2 |
|
|
|||
соображений, что и для однослойной стенки
|
|
1 |
i |
i |
|
|
tc i 1 tж1 |
|
|
|
|||
|
|
|||||
q |
1 |
|
|
|||
|
|
1 |
i |
|||