Свободные колебания в поле постоянной силы

На материальную точку кроме упругой силы, действует сила постоянная по величине и направлению.

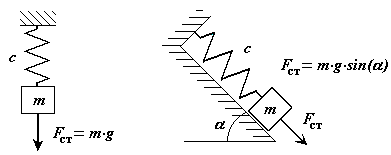
Рис. 2-4

Обозначим ее , тогда дифференциальное уравнение движения точки примет вид:

или , где

Начальные условия имеют вид: при , .

Это неоднородное дифференциальное уравнение. Его решение складывается из решения однородного дифференциального уравнения и частного решения неоднородного дифференциального уравнения .

Решение имеет вид:

,

Если начало отсчета координаты сдвинуть на , , тогда в новой системе отсчета решение будет иметь вид:

,

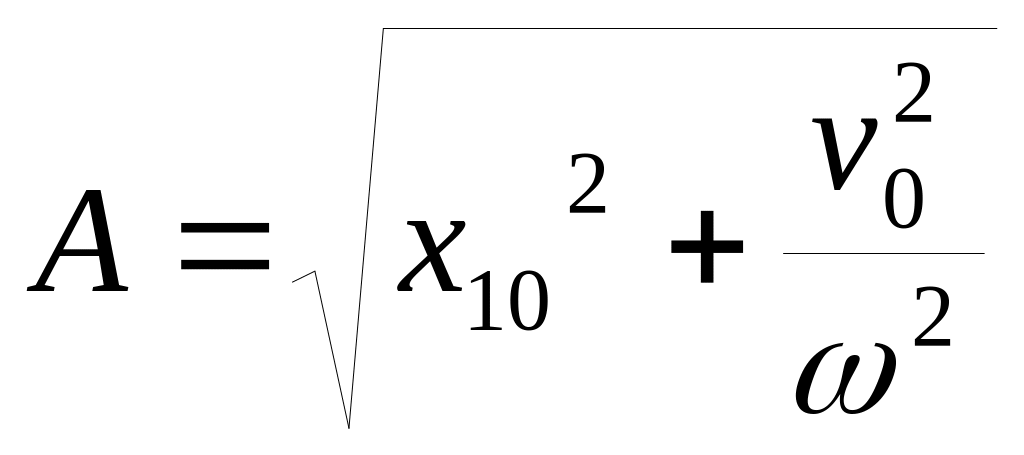- амплитуда колебаний;

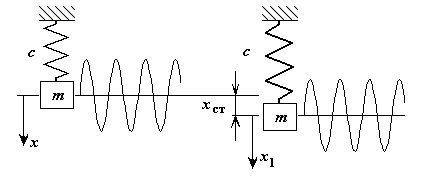
Рис. 2-5

Параллельное включение упругих элементов

Масса закреплена с помощью двух упругих элементов расположенных параллельно.

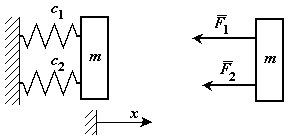
Рис. 2-6

Сместим массу на расстояние . , ,

Результирующая жесткость упругих элементов расположенных параллельно равна сумме жесткостей этих элементов..

Последовательное включение упругих элементов

М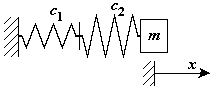 асса закреплена с помощью двух упругих элементов расположенных последовательно.

Рис. 2-7

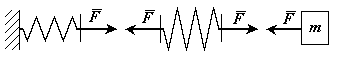
Рис. 2-8

Сместим массу на расстояние . В упругих элементах возникает восстанавливающая (упругая) сила , одинаковая для обоих элементов. Первый упругий элемент изменит длину на , второй - на . . , , .

, следовательно

Обратная величина результирующей жесткости упругих элементов расположенных последовательно равна сумме обратных величин жесткостей этих элементов.

Обратная величина жесткости упругого элемента называется податливостью этого элемента.

, , ,

Результирующая податливость упругих элементов расположенных последовательно равна сумме податливостей этих элементов..

Вынужденные колебания без сопротивления

Рассмотрим движение точки под действием двух сил: одна восстанавливающая, другая зависит от времени. - гармоническая возмущающая сила.

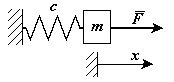- амплитуда возмущающей силы.

- круговая частота возмущающей силы.

Рис. 2-9

Дифференциальное уравнение движения точки с массой , закрепленной на упругом элементе, под действием возмущающей гармонической силы имеет вид:

Задавая решение уравнения в виде: и подставляя его в дифференциальное уравнение получим алгебраическое уравнение для определения амплитуды вынужденных колебаний.

.

Разделим его на массу и обозначим , тогда и окончательно

- амплитуда вынужденных колебаний.

- частота собственных колебаний

Материальная точка колеблется с амплитудой и частотой возмущающей силы .

Построим зависимость модуля амплитуды от частоты возмущающей силы .

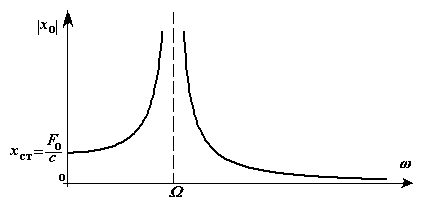
Рис. 2-10

Модуль амплитуды вынужденных колебаний возрастает от (при ) до бесконечности (при ) и убывает от бесконечности (при ) до нуля (при ).

Явление, когда частота возмущающей силы совпадает с собственной частотой колебаний системы, называется резонансом.