
Статика и кинематика / Теоретическая механика
.pdf71
на систему (как внешних, включая реакции связей, так и внутренних) на действительном элементарном перемещении этой системы.
n |
r |
r |
|
dT = ∑(Fke drk ) |
(2.23) |
||
k =1
Теорема об изменении кинетической энергии системы матери-
альных точек (в интегральной форме). Изменение кинетической энергии системы равно сумме работ всех сил, действующих на систему (как внешних, включая реакции связей, так и внутренних) на данном переме-
щение системы.
T −T = |
n |
r |
n |
r |
(2.24) |
∑ |
A(F e )+ |
∑ |
A(F i ). |
||
0 |
k |
k |
|
||
|
k =1 |
|
k =1 |
|
|
Замечание о работе внутренних сил. Для неизменяемой системы материальных точек. (в частности, для твердого тела) работа внутренних с при любом действительном перемещении системы равна нулю. Для неизменяемой системы (2.24) запишется в виде:
n r |
(2.25) |
T − T0 = ∑ A(Fke ) |
k=1
3.Принцип Даламбера. Элементы аналитической механики.
3.1.Принцип Даламбера.
Пусть точка механической системы движется под действием некоторой системы сил (эти силы могут быть разбиты либо на внешние и внутренние, либо на активные и силы реакций связей). Равнодействующую этой системы сходящихся сил обозначим F .
Силой инерции точки называется векторная величина F ин , равная произведению массы точки на ее ускорение и направленная противоположно ускорению:
F ин |
r |
= −ma |
Сила F ин фиктивна, она не входит в число реальных сил, действующих на точку.
Принцип Даламбера для материальной точки: силы, действую-
щие на материальную точку, и сила инерции в любой момент времени образуют систему сил, эквивалентную нулю, то есть находящуюся в равновесии.
F + F ин = 0
Принцип Даламбера для механической системы: внешние силы,
действующие на механическую систему, и силы инерции в любой момент
72
времени образуют систему сил, эквивалентную нулю, то есть находящуюся в равновесии.
В соответствии с этим принципом, если к каждой точке системы до-
бавить силу |
F ин = −m |
r |
|
, то система сил, состоящая из внешних F e |
и фик- |
|
a |
k |
|||||
|
k |
k |
|
k |
|
|
тивных F ин |
сил, будет удовлетворять всем уравнениям статики, т.е. глав- |
|||||
k |
|
|
|
|
|
|
ный вектор системы сил и ее главный момент относительно произвольного центра О будут равны нулю:
m r |
n r |
, |
∑ Fi e + ∑ Fkин = 0 |
||
m r
∑ M
i=1
i=1 |
k =1 |
|
r |
n r |
r |
O (Fi e )+ ∑ M O |
(Fkин )= 0 . |
|
k =1
В координатной форме эти уравнения записываются так:
m |
n |
m |
r |
n |
|
r |
∑ Fixe + ∑ Fkxин = 0 |
∑ M x (Fi e )+ ∑ M x |
(Fkин )= 0 |
||||
i=1 |
k =1 |
i=1 |
r |
k =1 |
|
r |
m |
n |
m |
n |
|
||
∑ Fiye + ∑ Fkyин = 0 |
∑ M y |
(Fi e )+ ∑ M y |
(Fkин )= 0 |
|||
i=1 |
k =1 |
i=1 |
r |
k =1 |
|
r |
m |
n |
m |
n |
|
||
∑ Fize + ∑ Fkzин = 0 |
∑ M z |
(Fi e )+ ∑ M z |
(Fkин )= 0 . |
|||
i=1 |
k =1 |
i=1 |
|
k =1 |
|
|
Принцип Даламбера позволяет перенести методы решения задач статики на задачи динамики.
Систему сил инерции, приложенных к точкам системы можно привести к силе и паре сил, а именно к главному вектору сил инерции
r |
n r |
|
|
|
|
Rин |
= ∑ Fkин , приложенному в заданном центре О, и главному моменту сил |
||||
|
k =1 |
r |
n r |
r |
|
инерции относительно этого центра |
|||||
M 0ин |
= ∑ M 0 |
(Fkин ). |
|||
k =1
Можно показать, что Rин при любом движении системы (твердого тела) подсчитывается по формуле:
r |
, |
Rин = −maC |
где m - масса системы, aC - ускорение центра масс.
Выражения для главного момента сил инерции твердого тела и его проекций на координатные оси:
1.При поступательном движении: M Cин = 0 .
2.При вращении вокруг неподвижной оси z: M zин = I z ε .
3.При плоскопараллельном движении: M Cин = IC ε . Здесь ε - угловое
ускорение тела, Iz и Iс - моменты инерции тела относительно оси z и оси, проходящей через центр масс перпендикулярно основной плоскости.
Моменты инерции M zин и M Cин направлены противоположно угловому ускорению ε .
73
3.2. Классификация механических связей. Обобщенные координаты.
Классификация механических связей. Механическими связями на-
зываются некоторые устройства (тела), накладывающие ограничения на положения и скорости точек механической системы. Эти ограничения выполняются всегда независимо от заданных сил и записываются в виде соотношений, называемых уравнениями связей.
Стационарными связями называются связи, не зависящие от времени; связи, зависящие от времени, называются нестационарными.
Связи, в уравнения которых входят координаты точек и время, называются геометрическими. Связи называются кинематическими (дифференциальными), если в уравнения связей входят скорости, координаты точек и время.
Если кинематическую связь можно «заменить» эквивалентной геометрической, то она называется кинематической интегрируемой, в противном случае – неинтегрируемой.
Геометрические и кинематические интегрируемые связи называются голономными, а кинематические неинтегрируемые - неголономными. Механическая система называется голономной, если на нее наложены только голономные связи, и неголономной, если имеется хотя бы одна неголономная связь.
Связи называются неосвобождающими, если ограничения, накладываемые ими на положения точек, их скорости и время, могут быть записаны в форме равенств. Освобождающие связи записываются в форме неравенств.
Возможным (виртуальным) перемещением точки механической системы называется воображаемое, бесконечно малое, допускаемое наложенными связями перемещение δr из положения, занимаемого точкой в данный момент времени.
Для стационарных связей действительные перемещения точек находятся среди возможных.
Механическая система может иметь множество различных возможных перемещений. Однако для систем, состоящих из материальных твердых тел и конечного количества материальных точек, существует некоторое число независимых между собой возможных перемещений, через которые можно выразить любое другое возможное перемещение. Число независимых перемещений называется числом степеней свободы механиче-
ской системы.
Обобщенными координатами называются независимые между собой переменные, которые однозначно определяют положение каждой точки механической системы. В случае голономной системы число степеней
74
свободы равно числу обобщенных координат, в случае неголономной системы число степеней свободы меньше числа обобщенных координат.
Идеальные связи. Связи называются идеальными, если сумма работ их реакций Ri равна нулю на любом возможном перемещении системы:
∑δA(Ri )= 0 .
i
Любой сложный механизм, состоящий из нескольких твердых тел, можно трактовать как механическую систему с идеальными связями, если тела соединены абсолютно жестко, при помощи идеальных шарниров (без трения), невесомыми нерастяжимыми идеально гибкими нитями. Кроме того, поверхности соприкосновения должны быть либо абсолютно гладкими, если одно тело скользит по поверхности другого, либо идеально шероховатыми, когда одно из тел катится по поверхности другого без проскальзывания.
3.3 Принцип возможных перемещений.
Рассмотрим задачу о равновесии механической системы. При наличии связей уравнения равновесия механической системы, получаемые геометрическим методом, кроме активных сил содержат еще и реакции связей. Число подлежащих определению реакций тем больше, чем больше связей ограничивают исследуемую систему. Естественно искать такие условия равновесия, которые не содержали бы реакции связей. Эти условия могут быть получены с помощью принципа возможных перемещений.
Принцип возможных перемещений является принципом, устанавливающим необходимые и достаточные условия равновесия системы материальных точек, а именно:
Необходимым и достаточным условием равновесия системы материальных точек с идеальными связями, является равенство нулю суммы работ всех активных сил, действующих на точки системы, на любом возможном перемещении системы, т.е.
n |
r |
(3.1) |
∑δA(Fi a )= 0 . |
||
i=1
3.4.Общее уравнение динамики.
Принцип Даламбера и принцип возможных перемещений определя-
75
ют общее уравнение динамики, что можно сформулировать следующим образом: в каждый момент движения механической системы с идеальными связями сумма элементарных работ всех активных сил и даламберовых сил инерции на любом возможном перемещении точек материальной системы равна нулю.
n |
r |
n |
r |
ин )= 0 . |
(3.2) |
∑δA(Fi a )+ ∑δA(Fi |
|||||
i=1 |
|
i=1 |
|
|
|
Уравнение (3.2) представляет собой общее уравнение динамики. Оно называется также уравнением Даламбера - Лагранжа.
Для голономной системы количество этих уравнений будет равно числу степеней свободы этой механической системы.
3.5. Уравнения Лагранжа второго рода.
Для описания движения голономной механической системы. с п степенями свободы, на·которую наложены идеальные связи, бывает удобно использовать уравнения Лагранжа второго рода:
d |
|
∂T |
|
|
∂T |
|
|
( j =1, 2,KS) . |
|
|
|
|
|
− |
|
= Q j |
, |
(3.3) |
|
|
& |
|
|||||||
dt |
|
|
|
∂q j |
|
|
|
|
|
|
∂q j |
|
|
|
|
|
|||
Здесь q j - обобщенные координаты. количество которых равно числу степеней свободы S, q& j - обобщенные скорости, равные производным по времени от обобщенных координат, T - кинетическая энергия системы, Q j - обобщенные силы. Уравнения Лагранжа второго рода получают-
ся из общего уравнения динамики, при переходе к·обобщённым координатам, путём математических преобразований.
Величины T и Q j должны быть представлены в виде функций обобщенных координат, обобщенных скоростей и времени:
|
|
|
& |
& |
T = T (q1 ,K, qS , q1 ,K, qS , t ) , |
||||
|
|
|
& |
& |
Q j = Q j (q1 ,K, qS , q1 |
,K, qS , t) . |
|||
Обобщенные силы находятся из выражения для суммы элементар- |
||||
ных работ активных сил F a |
на возможном перемещении системы, преоб- |
|||
i |
|
|
|
|
разованного к виду: |
|
|
|
|
|
r |
r |
r |
S |
|
|
|||
∑δA(Fi a )= ∑ Fi a |
δr = ∑Q j δq j . |
|||
i |
|
i |
|
j =1 |
Количество обобщенных сил равно числу степеней свободы S.
76
Преимущество уравнений Лагранжа второго рода состоит в том, что они получаются из выражения для кинетической энергии, а для ее вычисления нужно определить скорости точек механической системы. Методы определения этих скоростей изучены в кинематике.
77
РАСЧЕТНО-ГРАФИЧЕСКИЕ РАБОТЫ ЗАДАНИЕ С-2
Определение реакций опор составной конструкции.
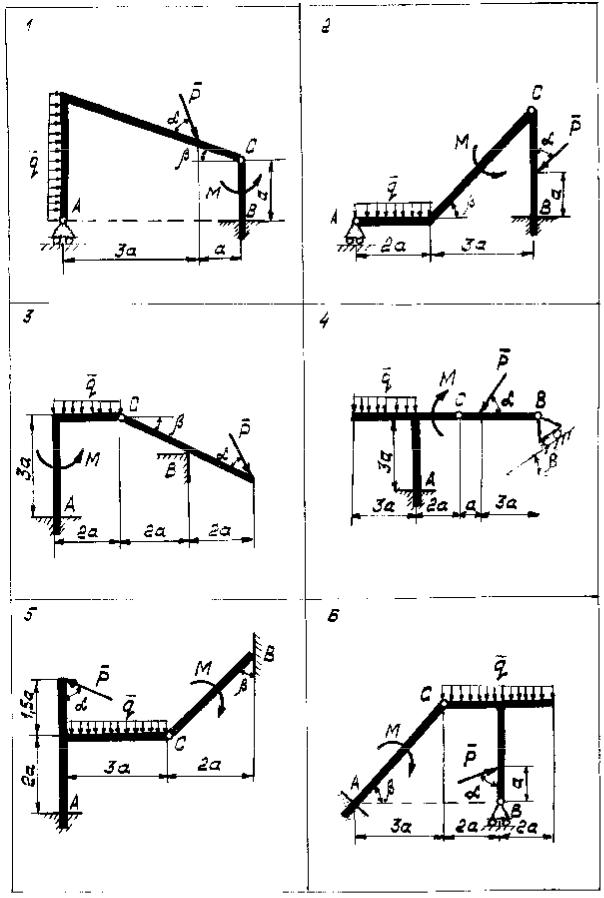
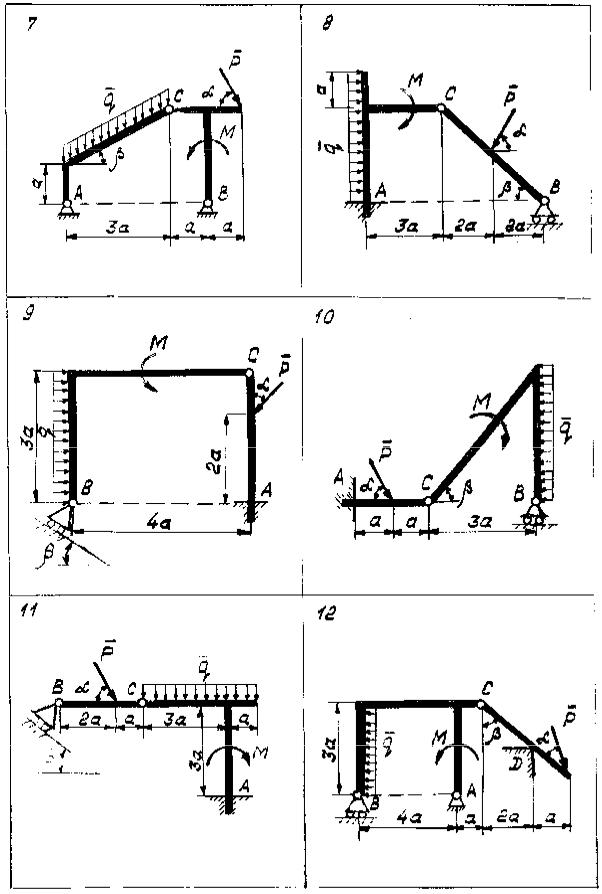
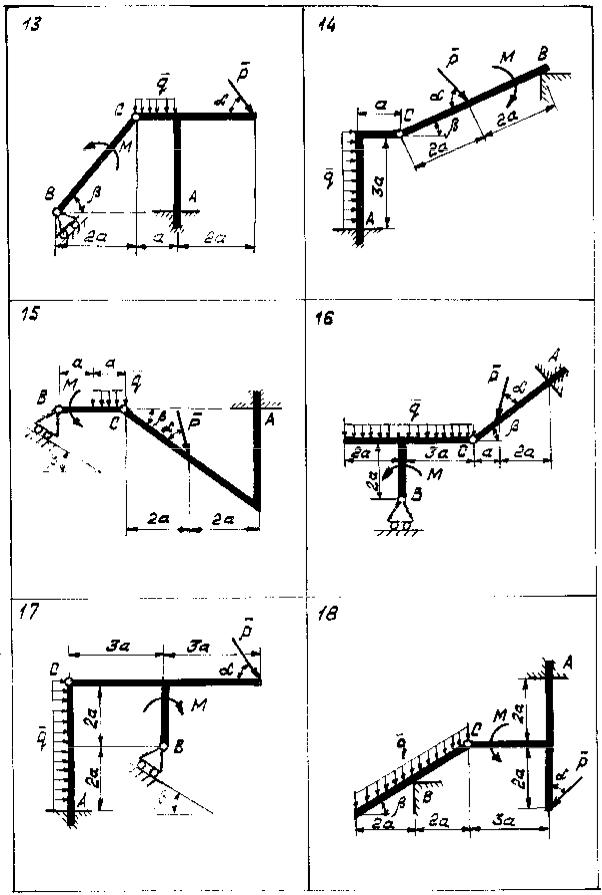
Определить реакции опор и давление в промежуточном шарнире C заданной составной конструкции. Схемы конструкции представлены на рис. 2.1–2.5, а необходимые данные - в таблице 2.
|
|
|
|
|
|
Таблица 2 |
№№ |
P, |
М, |
q, |
a, |
α, |
β, |
п/п |
кН |
кН·м |
кН/м |
м |
град. |
град. |
1 |
10 |
5 |
1,4 |
1,0 |
45 |
30 |
2 |
12 |
8 |
1,0 |
2,0 |
60 |
15 |
3 |
15 |
4 |
0,8 |
1,5 |
30 |
15 |
4 |
14 |
6 |
1,8 |
1,0 |
75 |
30 |
5 |
20 |
4 |
1,4 |
2,0 |
60 |
15 |
6 |
16 |
10 |
1,2 |
1,0 |
30 |
15 |
7 |
18 |
8 |
1,6 |
1,5 |
60 |
30 |
8 |
20 |
12 |
2,2 |
1,0 |
75 |
30 |
9 |
22 |
6 |
1,2 |
2,0 |
45 |
30 |
10 |
30 |
8 |
2,4 |
1,5 |
30 |
15 |
11 |
10 |
5 |
1,4 |
1,0 |
45 |
30 |
12 |
12 |
8 |
1,0 |
2,0 |
60 |
15 |
13 |
15 |
4 |
0,8 |
1,5 |
30 |
15 |
14 |
14 |
6 |
1,8 |
1,0 |
75 |
30 |
15 |
20 |
4 |
1,4 |
2,0 |
60 |
15 |
16 |
16 |
10 |
1,2 |
1,0 |
30 |
15 |
17 |
18 |
8 |
1,6 |
1,5 |
60 |
30 |
18 |
20 |
12 |
2,2 |
1,0 |
75 |
30 |
19 |
22 |
6 |
1,2 |
2,0 |
45 |
30 |
20 |
30 |
8 |
2,4 |
1,5 |
30 |
15 |
21 |
10 |
5 |
1,4 |
1,0 |
45 |
30 |
22 |
12 |
8 |
1,0 |
2,0 |
60 |
15 |
23 |
15 |
4 |
0,8 |
1,5 |
30 |
15 |
24 |
14 |
6 |
1,8 |
1,0 |
75 |
30 |
25 |
20 |
4 |
1,4 |
2,0 |
60 |
15 |
26 |
16 |
10 |
1,2 |
1,0 |
30 |
15 |
27 |
18 |
8 |
1,6 |
1,5 |
60 |
30 |
28 |
20 |
12 |
2,2 |
1,0 |
75 |
30 |
29 |
22 |
6 |
1,2 |
2,0 |
45 |
30 |
30 |
30 |
8 |
2,4 |
1,5 |
30 |
15 |
78
Рис. 2.1
79
Рис. 2.2
80
Рис. 2.3
