Лекции 4 сем в pdf по ТОЭ

4.6Процедура аналитически-численного анализа динамики нелинейных цепей

1.Выбираем модель, которой замещаем исследуемую цепь.

2.Выбираем соответствующие этой модели функции, которыми аппроксимируем нелинейные характеристики элементов цепи.

3.Описываем динамику составленной модели уравнением (4.1).

4.Описываем искомые точные решения обобщенными функциями с регулярными составляющими в виде функционально-степенных рядов.

5.Используя соответствующие формулы, перестраиваем исходное уравнение к виду

A D x t G D f t T t .

6.Выполнив над полученным уравнением преобразование Лапласа формируем уравнение

A p X p C p .

7.Последовательно записываем решения этого уравнения в виде соответствующих формул.

8.Вычисляем коэффициенты этого решения по соответствующим формулам и переводим результат в t-область.

9.При t 0 проверяем одно из трех условий существования решения.

10.Задаем уровень ε h предельной абсолютной локальной погрешности, выбираем одну из верхних оценок этой погрешности и соответствующую величину первого шага расчета.

11.Выполняем численную часть метода.

12.Результатом аналитически-численного расчета является область, содержащая неизвестное

12

5 Собственные теоремы теории электрических цепей

5.1Метод эквивалентных преобразований источников

5.1.1Назначение метода

Метод предназначен для частичного изменения структуры цепи и правой части ее уравнений динамики.

5.1.2Общий случай метода

Примечание. Поскольку эти теоремы пригодны для алгебраических описаний цепи, то изложение далее будет идти в p-области.

Примечание. Эквивалентность относительно выделенных зажимов здесь и далее означает, что все то, что происходит вне этой выделенной ветви или части цепи, может быть различным, а все то, что происходит в выделенной ветви или части цепи — одинаковым. Иными словами: если все, что находится слева от зажимов, поместить в «черный ящик», то пользуясь лишь зажимами 1 и 2 мы не сможем определить, какая цепь находится в «ящике».

Доказательство.

5.1.3Исключительный случай метода

5.1.3.1 Расщепление ветви

Z2 p

2

13

В таком случае источник может быть преобразован с помощью искусственного приема, называемого

расщеплением ветви:

2

Мы ничего не нарушили, поскольку в преобразованной цепи I0(p) = 0 по закону токов Кирхгофа:

I p I0 p I p 0 I0 p 0 .

После расщепления ветви источники тока легко преобразуются в источники напряжения:

1

Z1 p

Z2 p

2

5.1.3.2 Расщепление узла

Как видно из общего случая, для того, чтобы источник напряжения преобразовать в источники тока, надо иметь параллельный ему резистор.

В этом случае прибегнем к искусственному приему, называемому расщеплением узла:

В этом случае мы ничего не нарушили, поскольку U 00 0 по уравнению Кирхгофа для контура:

U p U00 U p 0 U00 0 .

14

Сначала выразим токи в цепи через контурные токи:

I1 p I1K p I3K pI 2 p I1K p I 2K p

I3 p I 2K p I3K p .I 4 p I3K p

I5 p I 2K p

I 6 p I1K p

Затем запишем уравнения Кирхгофа для выбранных независимых контуров и контурных токов:

Мы получили три уравнения для независимых контуров с четырьмя неизвестными. Теперь, если вместо истинных токов подставить их выражения через контурные токи, получим систему из трех уравнений с тремя неизвестными. Эта система будет линейно независимой.

Теперь запишем эти уравнения в матричной форме:

Z p IK p U p .

Очевидно, мы получили уравнение Ома в матричной форме. Если изучить содержимое этих матриц, то можно определить правила формирования матричного уравнения Ома:

a) Матрица собственных сопротивлений контуров Z p

Zii p — собственные сопротивления i-го контура. Эти собственные сопротивления представляет

собой суммы сопротивлений ветвей, образующих i-ый контур. Эти собственные сопротивления всегда имеют знак плюс.

Zik p — взаимные сопротивления i-го и k-го контуров ( i k ). Они образуются как сумма

сопротивлений ветвей общих для i-го и k-го контуров. Эта сумма имеет знак плюс, если в этих ветвях контурные токи со направлены и знак минус, если они направлены встречно.

Влинейных цепях Zik p Zki p .

b)Матрица-столбец напряжений источников напряжения U p

Это матрица-столбец источников напряжения, входящих в независимые контуры. В каждой строке этой матрицы содержится сумма напряжений источников напряжения, входящих в i-ый контур. Эти напряжения входят со знаком «+», если при обходе контура в выбранном нами направлении первой встречаем отрицательную клемму источника напряжения, и со знаком «−», если при обходе контура первой встречаем клемму, отмеченную знаком «+».

c)Матрица-столбец искомых контурных токов I K p . Это матрица-столбец — вектор искомых контурных токов.

Из записанного правила вытекает, что для составления матричного уравнения Ома нет

необходимости в предварительном формировании уравнений для независимых контуров через токи ветвей. Отсюда следует процедура анализа линейных пассивных планарных и непланарных цепей методом контурных токов.

1.Преобразуем все допускающие такое преобразование источники тока в эквивалентные им источники напряжения. Если какой-либо источник тока эквивалентно не преобразовать в источник напряжения, то это исключительный случай метода.

2.Обычным образом формируем одну из систем независимых контуров (формируем граф, дерево, ветви связи и т.д.).

3.Назначаем систему контурных токов, указывая их направления обхода независимых контуров и нумеруя их, то есть формируем вектор I K p .

4.По описанному правилу формируем матрицы Z p и U p .

5.Составленное матричное уравнение Ома обычным образом проверяем на существование и единственность решения. Далее обычным образом решаем его относительно контурных токов.

6.На основании постулата Кирхгофа для узлов составляем систему уравнений связи между контурными токами и токами ветвей.

7.Полученный результат переводим в t-область и проверяем, записав в t-области уравнения Кирхгофа для независимых контуров и узлов.

16

Примечание. Благодаря глубокой формализации МКТ решение в p-области можно записать сразу, минуя составление матричного уравнения Ома.

5.2.4Исключительный случай МКТ (линейные пассивные планарные и непланарные цепи)

Из постановки задачи и сформированного правила составления матричного уравнения Ома вытекает, что исключительным случаем метода будет такой, когда в цепи есть один или несколько источников тока, не преобразуемых эквивалентно в источники напряжения.

В этом случае необходимо систему независимых контуров назначить так, чтобы каждая ветвь, содержащая непреобразуемый источник тока, принадлежала только одному контуру. Тогда соответствующий контурный ток, сонаправленный или противоположно направленный с этим источником тока, будет заведомо известен. Кроме того, в силу определения источника тока, соответствующее собственное сопротивление этого контура не определено и поэтому, формально составив уравнения Ома для выбранной системы независимых контуров, мы должны вычеркнуть из нее строки и столбцы, принадлежащие непреобразуемым источникам тока (уже известным контурным токам). Члены левой части уравнения, стоящие в остальных строках, вычеркиваемых столбцов, переносим в правую часть. Полученную систему уравнений далее решаем обычным образом.

5.2.5 Особенности расчета линейных активных планарных и непланарных цепей в общем и исключительном случаях метода

По определению, МКТ в общем случае требует наличия источников напряжения, а неизвестными являются токи. Отсюда вывод: ИНУТ подходит сразу, ИТУН можно легко преобразовать в ИНУТ. ИТУН — наихудший вариант, поскольку потребуется преобразование и управляющего, и управляемого элемента. Преобразование ИТУТ тоже может вызвать затруднения.

Если окажется, что из ИТУТ/ИТУН источник не преобразуется, в силу вступает особый случай метода. В общем случае, если эквивалентное преобразование оказалось возможным, то по сравнению с пассивными цепями, наличие управляющего источника внесет соответствующие изменения в матричное уравнение Ома.

В остальном обе сформированные процедуры не претерпят изменений. Пример. Анализ активной линейной планарной резистивной цепи

U +

R4

R3

ИНУТ

+kI1R4

2

17

Приведем эту систему к виду Z IК = U:

Дальнейшее решение производится по Крамеру:

Примечание. Как легко видеть, характерной особенностью активных цепей оказывается несимметричность матрицы Z относительно главной диагонали. Кроме того, несложно проверить, что при

k R1 R2 R1 R3 R2 R3 R1 R4 R3 R4 R3 R4

главный определитель равен нулю. Таким образом, введение активного элементо коренным образом влияет на структуру даже линейных цепей.

5.2.6Расчет нелинейных активных и пассивных планарных и непланарных цепей

Основная особенность нелинейных цепей — возможность несуществования решения или его неединственности.

Наиболее простые нелинейные цепи такие, которые допускают кусочную линеаризацию своих характеристик. В этом случае их можно рассчитывать по методу контурных токов на каждом линейном участке и для каждого последующего участка использовать в качестве предначальных условий результат предшествующего расчета, а вновь полученное решение проверять на существование.

В остальном все сформулированные ранее процедуры (общий случай, исключительный случай, активные цепи) остаются без изменений.

5.2.7Достоинства и недостатки МКТ

5.2.7.1Достоинства

1.Существенное понижение размерности задачи благодаря ее декомпозиции.

2.Глубокая формализация задачи, благодаря которой после описания задачи в терминах контурных токов можно сразу же записывать ответ в виде отношения частного определителя к главному.

5.2.7.2Недостатки

1.Введение фиктивных переменных — контурных токов, не подчиняющихся постулату Кирхгофа для узлов.

2.Необходимость составления уравнений связи между контурными токами и истинными токами ветвей.

3.Необходимость определения знака взаимных сопротивлений в зависимости от направлений обхода контуров.

5.3Метод узловых напряжений (МУН)

5.3.1Назначение метода

Метод предназначен для анализа любых цепей: линейных и нелинейных, пассивных и активных, планарных и непланарных.

5.3.2Существо метода

Существо метода заключается в том, что в качестве искомых переменных мы выбираем напряжения независимых узлов, отсчитываемые от напряжения зависимого узла. Поскольку любая цепь содержит n узлов, из которых (n−1) независимых, то следовательно размерность задачи, решаемой МУН, всегда равна (n−1), то есть существенно меньше размерности задачи, решаемой с помощью постулатов Кирхгофа. Отметим то существенное обстоятельство, что узловые напряжения — это фактические, а не фиктивные переменные. И, следовательно, в МУН никакие уравнения связи и дополнительные вычисления не нужны.

5.3.3Общий случай метода

Из постановки задачи следует, что в общем случае цепь должна содержать только источники тока.

18

Рассмотрим следующую цепь (зависимый узел — 3):

Запишем уравнения Кирхгофа для независимых узлов 1 и 2:

Обычно, если это не оговорено в условии, напряжение зависимого узла принимают равным нулю. Тогда уравнения К. примут вид

Или, в матричной форме:

GU I .

Такую запись можно представить для любой цепи, если она содержит только источники тока.

Полученное уравнение есть уравнение Ома в матричной форме.

Сформируем правила, которым подчиняются элементы этого уравнения.

a)Матрица проводимости G

Элементы, находящиеся на главной диагонали Gii называют собственными проводимостями i-го узла. Она равна сумме проводимостей всех ветвей подключенных к i-му узлу. Остальные элементы Gij ( i j ) называют взаимными проводимостями между i-м и j-м узлами. Gij равно сумме проводимостей всех ветвей, соединяющих i-ый и j-ый узлы, взятой со знаком минус.

b)Матрица-столбец токов источников тока I

В k-й строке столбца I стоит сумма токов источников тока, подключенных к k-му узлу. Члены этой суммы берутся со знаком плюс, если соответствующие токи втекают в k-ый узел, и со знаком минус, если вытекают.

c)Матрица-столбец искомых узловых напряжений U

Матрица U содержит искомые напряжения независимых узлов.

Сформируем процедуру метода узловых напряжений для линейных пассивных цепей в общем

случае:

1.Преобразуем все допускающие преобразование источники напряжения в источники тока. Если в цепи есть не преобразуемые источники напряжения, то это исключительный случай метода.

2.Обычным образом формируем систему независимых узлов. Если никаких дополнительных указаний нет, то удобно напряжение зависимого узла принять равным нулю.

3.Назначаем номера независимых узлов, то есть формируем матрицу U.

4.По описанным правилам формируем матрицу I.

5.Составленное матричное уравнение Ома обычным образом решаем относительно узловых напряжений.

6.Если необходимо, то по найденным узловым напряжениям вычисляем токи ветвей.

7.Обычным образом проверяем полученный результат.

5.3.4Исключительный случай метода (линейные пассивные цепи)

Поскольку метод узловых напряжений требует наличия только источников тока, то исключительный случай метода будет тогда, когда в цепи есть не преобразуемые эквивалентно источники напряжения. В отличие от метода контурных токов, для которого безразлично число непреобразуемых источников тока, в методе узловых напряжений число непреобразуемых источников напряжения существенно.

Рассмотрим два случая: когда в цепи один непреобразуемый источник напряжения и когда в цепи более одного непреобразуемого источника напряжения.

5.3.4.1 Один непреобразуемый источник напряжения

В этом случае один из зажимов непреобразуемого источника принимаем в качестве зависимого узла. k

+

U

19

Тогда, составив формально систему уравнений по методу узловых напряжений, мы обнаружим следующую

ситуацию:

... Gk 1,kU k ...

... Gk ,kU k ...

... Gk 1,kU k ...

Собственная проводимость Gk ,k неопределима, но зато Uk U . В таком случае мы можем вычеркнуть k-ю

строку и k-ый столбец. Все члены, принадлежащие k-му столбцу, кроме k-ой строки, переносим вправо.

Размерность системы уменьшится, совместность сохранится.

5.3.4.2 Более одного непреобразуемого источника напряжения (например, два)

В этом случае с одним из этих источников поступают так, как в предыдущем пункте. А второй непреобразуемый источник напряжения формально заменяют фиктивным источником тока:

+

I

Тогда получим в системе уравнений МУН

... I ... n - я строка

... I ... (n 1) - я строка

Сложив n-ю и (n+1)-ю строки, получим

... I I ...

Отметим, что добавленный нами фиктивный источник тока, присоединенный к n-му и (n+1)-му независимым узлам, очевидно, не присоединен ни к каким другим и поэтому входит только в правые части n-го и (n+1)-го уравнений.

Но полученная система уравнений оказывается несовместной, потому что в ней число искомых переменных стало на единицу больше числа уравнений. Следовательно, переформированную систему необходимо дополнить ещѐ одним линейно независимым уравнением. Им будет уравнение Кирхгофа для независимого контура, куда входит U:

... U n U n 1 U ... 0 .

Дополненная таким образом система уравнений становится совместной, и далее решается обычным образом.

5.3.5Линейные планарные и непланарные активные цепи

Для применения метода узловых напряжений в цепи должны присутствовать только источники тока управляемые напряжением (ИТУН). Остальные источники надо преобразовать к этому виду источника. Иначе вступает в силу исключительный случай метода.

5.3.6Расчет планарных и не планарных пассивных и активных нелинейных цепей

В нелинейных цепях возможна множественность решений. При этом, в множестве полученных решений только некоторое подмножество действительно удовлетворяет поставленным условиям задачи.

В случае нелинейных цепей МУН сводится к записи уравнений Кирхгофа для независимых узлов, описывающих нелинейные характеристики входящих в цепь элементов через узловые напряжения.

5.3.7Достоинства и недостатки МУН

5.3.7.1Достоинства

1.Существенное понижение порядка анализируемой системы уравнений до (n−1), где n — количество узлов.

2.В отличие от МКТ, оперирует с физически существующими величинами — напряжениями независимых узлов. Следовательно, отпадает необходимость в уравнениях связи.

3.Элементы матрицы проводимостей G имеют фиксированные знаки (на главной диагонали у всех «+», вне нее у всех «−»). Таким образом, в отличие от МКТ, не нужно учитывать знаки у коэффициентов Gij.

5.3.7.2Недостатки

Недостатков у метода нет. Он совершенен и потому столь часто используется как база для неосновных собственных теорем теории электрических цепей.

20

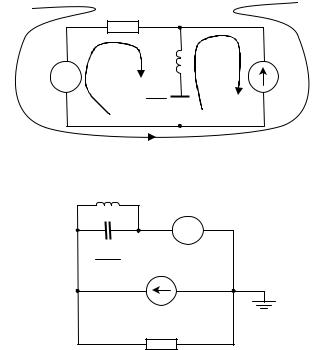
5.4Дуальность (двойственность) линейных электрических цепей

Метод контурных токов и метод узловых напряжений позволили обнаружить, что всякой линейной электрической цепи можно сопоставить другую линейную электрическую цепь, которую с точностью до обозначений элементов описывают такие же уравнения, но в методе контурных токов или, напротив, в методе узловых напряжений. Дело в том, что матричные уравнения МКТ и МУН: RI = U и GU = I с точностью до обозначений совпадают.

Для составления этой цепи необходимо, чтобы число контуров одной цепи было равно числу независимых узлов другой. И тогда, в соответствии с матричными уравнениями Ома RI U и GU I , можно записать процедуру дуального перехода от одной цепи к ее дуальной. Сформулируем эту процедуру для линейных планарных цепей, при переходе от описания по методу контурных токов к описанию по методу узловых напряжений.

1.В качестве независимых контуров выбираем элементарные ячейки графа цепи и назначаем одинаковые, по или против часовой стрелки, направления обхода этих независимых контуров. (Это делаем для того, чтобы избежать недостатка метода контурных токов, связанного со знаками взаимных сопротивлений. Наш выбор дает возможность непосредственного перехода от взаимных сопротивлений к проводимостям).

2.Для того, чтобы образовать зависимый узел, необходимо назначить еще и зависимый контур. В качестве зависимого контура выбираем все внешнее по отношению к цепи пространство с тем же направлением его обхода.

3.Назначаем систему независимых узлов, соответствующих независимым контурам и зависимый узел, соответствующий зависимому контуру.

4.Соединяем независимые узлы и зависимый дуальными исходной цепи элементами, численно им равными и дуально включенными.

5.Полярность источников напряжения и направление тока источников тока в дуальной цепи выбираем так, чтобы обеспечить их вхождение в правые части в новой системе уравнений с теми же знаками, что и в исходной цепи.

Пример. Дуальное преобразование линейной планарной пассивной цепи

pC

Назначаем узлы, два независимых и один зависимый, соответствующие независимым и зависимым контурам соответственно:

Эти цепи дуальны: если их описать МКТ и МУН соответственно, то эти описания совпадут с точностью до обозначений.

21