
Частина 4
.pdf
“Курс вищої математики. Частина 4.”
На графі не наголошується ймовірність переходу системи з одного стану в те ж саме. При розгляді конкретних систем зручно спочатку побудувати граф станів, потім визначити ймовірність переходів системи з одного стану в те ж саме (виходячи з вимоги рівності одиниці суми елементів рядків матриці), а потім скласти матрицю переходів системи.
Хай Pij(n) – ймовірність того, що в результаті n випробувань система перейде із стану i в стан j, r – деякий проміжний стан між станами i і j. Ймовірність переходу з одного стану в інше pij(1)= pij.
Тоді ймовірність Pij(n) може бути знайдена по формулі, званій рівністю Марков:
k
Pij (n) = ∑Pir (m)Prj (n − m)
r =1
Тут т – число кроків (випробувань), за яке система перейшла із стану i в стан r. В принципі, рівність Марков є ні що інше як декілька видоизменная формула
повної ймовірності.
Знаючи перехідну ймовірність (тобто знаючи матрицю переходу Р1), можна знайти ймовірність переходу із стану в стан за два кроки Pij(2), тобто матрицю Р2, знаючи її – знайти матрицю Р3, і так далі
Безпосереднє застосувань отриманої вище формули не дуже зручно, тому, можна скористатися прийомами матричного числення (адже ця формула по суті – не що інше як формула перемножування двох матриць).
Тоді в загальному вигляді можна записати:
Pn = P1n
Взагалі те цей факт зазвичай формулюється у вигляді теореми, проте, її доказ достатній просте, тому приводити його не буду.
Приклад. Задана матриця переходів Р1. Знайти матрицю Р3.
|
|
|
|
|
|
0,1 |
0,9 |
|
|
|
|
||
|
|
|
|
|
P = |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,3 |
0,7 |
|
|
|
|
||
|
P |
|
0,1 0,9 0,1 |
0,9 |
= |
|
0,28 |
0,72 |
|
||||
|
= |
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
0,3 |
|
|
|
|
0,24 |
|
|
|
|
|
0,3 0,7 |
0,7 |
|
|
0,76 |
|
|||||
P |
= |
0,1 |
0,9 0,28 |
0,72 |
= |
|
0,244 |
0,756 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
|
|
0,3 |
0,7 |
|
|
|
|
|
|
0,252 |
0,748 |
|
|
|
|
0,24 |
0,76 |
|
|
|
||||||
Визначення. Матриці, суми елементів всіх рядків яких рівні одиниці, називаються стохастичними. Якщо при деякому п всі елементи матриці Рп не рівні нулю, то така матриця переходів називається регулярною.
Іншими словами, регулярні матриці переходів задають ланцюг Марков, в якій кожен стан може бути досягнуте через п кроків з будь-якого стану. Такі ланцюги Марков також називаються регулярними.
61

“Курс вищої математики. Частина 4.”
Теорема. (теорема про граничну ймовірність) Хай даний регулярний ланцюг Марков з п станами і Р – її матриця ймовірності переходу. Тоді існує межа
lim Pn = P(∞)
n→∞
і матриця Р(∞) має вигляд:
u |
1 |
u |
2 |
... |
u |
n |
|
|
u |
... |
u |
|
|||
u |
1 |
2 |
n |
|
|||
P(∞) = |
|
|
|
|
|||
... ... |
... ... |
|
|||||
u |
1 |
u |
2 |
... |
u |
n |
|
|
|
|
|
|
|||
Тобто матриця складається з однакових рядків.
Тепер про величини ui. Числа u1, u2 ., un називаються граничною ймовірністю. Ця ймовірність не залежить від початкового стану системи і є компонентами власного вектора матриці РТ (транспонованою до матриці Р).
Цей вектор повністю визначається з умов:
PT ur = ur; ∑ui =1;
Приклад. Знайдемо граничну ймовірність для розглянутого выше прикладу.
0,1 |
0,9 |
|
0,1 |
0,3 |
|||
P = |
|
|
; |
PT = |
|
|
|
|
0,3 |
0,7 |
|
|
0,9 |
0,7 |
|
|
|
|
|
||||
|
0,1 |
0,3 |
u |
1 |
|
u |
1 |
|
|
|
|
|
|
|
= |
|
|
||
|
|
0,7 |
|
|
|
|
|
|
|
|
0,9 |
u |
2 |
|
u |
2 |
|
|
|
u1 |
= 0,1u1 + 0,3u2 |
|
0,9u1 |
= 0,3u2 ; |
u2 = 3u1 ; |
||||
u2 |
= 0,9u1 + 0,7u2 |
|
|||||||
|
|
|
|
|
|
|
|
||
C обліком того, що u1 + u2 = 1, отримуємо:
|
|
|
u1 +3u1 =1; |
u1 = 0,25; |
u2 = 0,75; |
|
Отримуємо: |
0,25 |
0,75 |
|
|
||
P(∞) = |
|
|
|
|
|
|
|
|
0,25 |
0,75 |
|
|
|
|
|
|
|
|
||
62
“Курс вищої математики. Частина 4.”
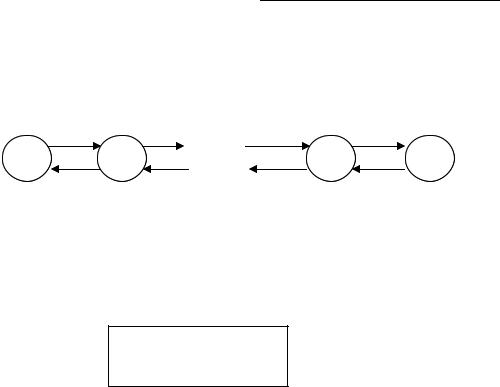
Процес загибелі – розмноження і циклічний процес.
Визначення. Марківський процес з дискретними станами називають процесом загибелі – розмноження, якщо він має размеченный граф состояний наступного вигляду:
λ12 |
23 |
n-2,n-1 |
n-1,n |
|
S1 |
S2 |
|
Sn-1 |
Sn |
λ21 |
32 |
n-1,n-2 |
n,n-1 |
|
Тобто кожен із станів системи пов'язаний з двома сусідніми станами прямим і зворотним зв'язком, крайні стани мають тільки поодинці сусідньому.
Тут λij – щільність ймовірності переходу системи із стану Si в стан Sj у момент
часу t.
Ця щільність знаходиться по формулі:
λij (t) = lim |
Pij (t, ∆t) |
|
∆t |
||
∆t→0+0 |
∆t – час переходу з одного стану в інше.
63

“Курс вищої математики. Частина 4.”
Зміст:
Теорія ймовірності. Основні поняття. Операції над подіями.
Теорема складання ймовірності. Умовна ймовірність.
Теорема множення ймовірності. Формула повної ймовірності. Формула Бейеса.
Повторення випробувань. Формула Бернуллі. Випадкові величини.
Закон розподілу дискретної випадкової величини. Біномінальний розподіл.
Розподіл Пуассона.
Числові характеристики дискретної випадкової величини. Математичне очікування.
Властивості математичного очікування. Дисперсія.
Обчислення дисперсії. Властивості дисперсії.
Середнє квадратичне відхилення. Функція розподілу. Властивості функції розподілу. Щільність розподілу. Властивості щільності розподілу.
Числові характеристики безперервної випадкової величини. Рівномірний розподіл.
Показовий розподіл. Нормальний закон розподілу. Функція Лапласа.
Правило трьох сигм.
Центральна гранична теорема Ляпунова. Система випадкових величин.
Щільність розподілу системи двох випадкових величин. Умовні закони розподілу.
Умовне математичне очікування. Залежні і незалежні випадкові величини. Лінійна регресія.
Лінійна кореляція. Закон великих чисел. Нерівність Чебишева. Теорема Чебишева. Теорема Бернуллі. Граничні теореми. Характеристичні функції.
Теорія масового обслуговування. Випадкові процеси.
Потік подій.
Нестаціонарний пуассоновский потік. Потік Пальма.
Потоки Ерланга. Ланцюги Марков.
Матриця переходів і граф станів. Гранична ймовірність.
Процес загибелі – розмноження і циклічний процес.
64
