Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B

мехде кутовимианiчнеiстатистичнедужкамипознач.Отжå,ноповнийповне перерiзусереднення квантово-

=

wAhA|ρ−q(0)ρq(t)|Ai = hρ−q(0)ρq(t) ,

A

m

2 1

N Z

dΩ Z

σ =

dω |νq |2k′S(q, ω),

823

2π~2

k

де величину

бельгiйськ S(q, ω)

трзенбезиваютьорльнуПркрольвиведiакзалежнiстьЛеонадинамiчперекинутиннiтеорi¨ункцi¹ю

S(q, ω) =

2π

Z−∞ dt e−iωthρ−q(0)ρq(t)

àéíò

гора¹.няiзикце

ðîöi

Ванцi¹¨непружногоийвiдова,ормулстручасуВаняктурнийовамиувiврозсiяннянавикористали¨¨честьакторвобiг.Величину. Вiн1954ображЗалежвiдi

q можна зробити замiну q на −q. Отже,

часу можна

íà

t

äëÿ

ператора

ρq

.

íiñòü âiä

оператор

¹ìî

ρ−q. Ó ðåç льтатi отрима-

альний перерiз розсiяння,перерiз

ÿêèéðîçñiÿííÿ

σ, уведемояекспериментально:двiчiди еренцi-

âèìiðþ¹òüñ

Крiм того, ця величина не залежитьпотенцiально¨вiд напрямку вектора

hρ−q(0)ρq(t)

= hρ−q(−t)ρq(0) .

оскiлькипiдсумовуваннiрозкладi

ðÿä Ôóð'¹

åíåð i¨

q,

ïðè

çà

U (|r − Rj |)

повний

= hρq(0)ρ−q(t) .

Маючиhρ−q(−t)ρq(0) = hρq(−t)ρ−q(0)

dΩdω =

k′

N 2π~2

νq

частинок,

S(q, ω)

d2σ

k

m

2

σ = Z

сядинзаВiнвщочнкодщо

dΩ Z

dω dΩ dω .

òàê

d2σ

-

яннякут з рщозрахункупотокуозсiюють.Якна

ористдорiвню¹йницюiнаòîеричасуâвiдношениразаленердлядиi¨,íамплiтудиицюдокiлькостiвеличинитiлеснðîçñiгопадаючого

íàáëèæåííi,

f в борнiвському

d2σ

k′

2

Справдi,

=

k N |f |

S(q, ω).

структуруНепружнеякщочовини,розспроiнтеянняакрувдiàñòòè¹ ðзмогууктурувизначити¨¨ енер етичногоякпросторовуспектра.

824

S(q, ω)

за всiма частотами ω,

∞

1

∞

∞

Z−∞ dω S(q, ω)

=

Z−∞ dt Z−∞ dω e−iωthρq(0)ρ−q(t)i

2π

∞

äå

=

Z−∞ dt δ(t)hρq (0)ρ−q(t)i = hρqρ−qi,

статичний стуктурний

актор. Таким чином,

Sq = hρq

ρ−qi,

горнутомуДалiдинамiчнийвиглядi:

Z−∞ dωS(q, ω) = Sq .

∞

структурний актор можна записати в роз-

S(q, ω) =

−∞

X

wAhA|ρ−qeiHˆ t/~ρqe−iHˆ t/~|Ai

2π Z

∞ dt e−iωt

A

1

1

−∞

X X

ðiâíiâ−

A|h

′|

q|

i|

~

A A′

=

X X

ðiçíèöi

(EA′−EA)t/~

2π Z

∞ dt e−iωt

A

A′

wAe

× hA|ρ−q|A′ihA′|ρq|A

Отже, величина=

w

A ρ A 2δ

ω

EA′

− EA

.

S(q, ω) ì๠δ-ïîäiáíi

пiки для частот ω =

íi, ÿê

ÿ ç àòîìiâ 3свинцюHe-208. У резуозсiю¹тьсльатiяцьогонамiшеядро825

208Pb переходить iз де кого початкового стану з е ер i¹ю

EA â

збуджений стан, енер iÿ ÿê ãî äîðiâíþ¹

тру¹ться приладами з енер i¹ю

EA′. Частиíêà 3He ðå¹ñ-

~2k′2

~2k2

äå

=

+ EA − EA′,

2m

2m

Äëÿ

2певного2

куткiнетичнарозсiянняенерзаiярiзницеюядра3He,енерякеiйпада¹

íà ìiøåíü.

~

k /2m

~2k2

~2k′2

,

ãî àê

наора,якiйвизначаютьспостерiга¹тьсяенер~максиω =

2m

−

2m

етичнийìóìспедиíàìi÷êòð ногоенерструктурн

-

îìó

ðîçñiÿíèõ. олу рiдквнимчас

аннемульсi¨нейтронiв.iйPb

ðîçñiÿííÿ

âçà¹ìî

инок,Iншиймузокремаекспериментiприкладзадовжиною¹цеточненепружневимiрютрекiв

208

òàê

випадкусукупнiстьнейтрон,.Тщобто нейтрондi¹звiякторадд ¹миенергiюатомiв

4

He,

4збуджу¹He. У цьомувсю ¨хню

iмпульс

~ω é

Ò ïîâq = kïiê′

динамiчногоk рiдинi як цiлструктурногому.

ðiäê ãî

4

чсiйнихють,мiрюванвиименто

−

ломленструктурозсподiблiнi¨(дивквантпереоренцiвськяння.атомаяийŸ64),iзуноготавомехструктурдонейтронiв,розсiяння,(диволиоюептанiчактораiцi¹нт.кривоювраховуватиŸ63)ихтамоделюî.нагаду¹дсистембтоЕкспепогли.перЛоНе,ви.

àíiâàáî

динамiчного

ç

ç

частотриво¨

арних

ийквазiстацiохарактерметодомïðîдвiчiрезонадляiëдипокудинамiчногоñнепружногоíтеренцiальногосiвськоюпектрально¨сних

çширенацiвськийжиттяченогоякпоблизуальнiормуправило,ям

ííÿ

€ уссiвський характер онтура

îãî àêòî

à

тепловi рухи атомiв. Тому в загальному випадку

-

Наормуютьiльетичнийарисавеличини.ссiвського78спектрзображенорiдконтурiвогоможнавизначений.залежнообразитиполозг женнямрткоюлоренцiвсьцихпiкiв

енеркогопро

S(q, ω)

4Íå

вiд хвильового вектора

овогоелементарнихвекторазбуджень.

q. ПроУдiлянцiцейспектрмалихговорятьзначеньяк прохвильспектр

описують звуковi олив ння, енер iя яких

q

c

åííÿ

кiсть звуку. Цi збудження називають

Eq

= ~qc

ононами. Бiля, точкишвид-

826

q =

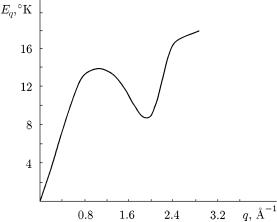
ис. 78. Енер етичний спектр рiдкого 4He.

q0

1.91 A−1 енер етичний спектр ма¹ аракте ний мiнiмум

пов'язНаспрахядку:дить нийâколидiiдякапомилковогомехзнайближчiiснуванням¹нiзмпорядкуK.Цiутвозбудженняпñðхередньоюусiдиенняиписуваарактерноговибраногоцi¹¨називаютьнямiжатомно¨резонансно¨¨мдлявиатомаõðîрiдинтонамивихвiдстдiлянкирозтближньогорухiвашованi.Назвауспектрарiдинiпо.

вiдстанi,

8.6◦

Eq0 =

тичний структурний актор ма¹ яскраво виражений п кaó,

ñò÷öi

q q0

-

кул,на прикладiенер(дивiя. рисполiенового¹пропорцiйною.51). У впорядковланцюжкдо нихткiльцевихструктурах,арактероргякчнихмибамолечили

ïðè

cos qa ìà¹

í резонанс

îсягстану¹ длямiнiмального. Перiдкший такийнульрезонанснийового знач

мiнiмумнястосовнонакривiйенер

точкиенерi¨лиосновногiянаiмпульсд qa = 2πn,

n = 1, 2, 3, . . . ,

спериментi4He ак ж пови ен виникати

îêîëi

спостерiга¹тьсрозташуваннi. Однак,атомiв,екунаслiдокцеймiнiмумх.арактерногоуж не дорiвню¹длярiдинулевiбез827-.

Целадуй q0

= 2π/a

у цей мехAанiзм, енняякда¹i¹

ймточкоювiрнiстьзакiнченнярозпаду

ïзбудженьектра.оловнийзенер i¹ювнесок

q 2.7

−1

на два збудж

åíåð iÿìè

2Δ

тобто на два ротони, що розлiт

хвильовими

q = q0

пiд кутом

закон збереж

iмпульсу да¹

θ = π/2. Причому

ìèùî

моментДинамiчнвiдповiда¹Ÿ 109

√

1

èйспостережуваномуструктурний. Динамiчнийакторструктурнийзначеннюповнiстю. визнача¹тьсяактор

Añâî¨-,

qc = 2q0 sin(θ/2) = q0

2 2.7

−

∞

n

n

Як ми бачили, нульовий момент,Неважколи

ω

=

Z−∞

ω S(q, ω)dω.

óíàñëiäîê

Sq .

о обчислити перший момент:

∞

1

∞

∞

ω¯ =

Z−∞ ωS(q, ω)dω =

2π

Z−∞ dt Z−∞ dω ωe−iωthρq(0)ρ−q(t)i

828енермушенiдзвенитьнема¹1Наведемо. iяБульбастацiонзвук

∞

∞

d

1

якихелихякщосильногозбуджуютьiзним¨хшампан¹загбагато,цокатисьасання,ькимвито-

Келихньцiомуспогрезонатористеми,лина¹тьсзiстоячихрезонаторами,звичайнимуякiй,ямають.хвилвином,згасання

оливаннячерезовихщерутворенняиххвильдин.Оскiлькишампанськстприкладсильноiв.вøêè

=

−2πi

Z−∞ dt Z−∞ dωhρq(0)ρ−q(t) dt e−iωt

динамiчний

N

~

2

X

e

2

q

2

Ó

отриму¹моˆ

√N q[ j , ρq] =

m .

результатi[[ρ−q, H], ρq] =

m

j=1

загйогоальномупiкмовипZ−∞

ωS(q, ω) dω = 2m .

∞

~q2

близуУ

жнадкузобразити лоренöåâструктурнийою кривою: актор по-

(вiдомий

q/2π

íåðà),

S(q, ω) = Sq

де велич на

q

âñiìàê

аналамичастотвиразе микцiйвiддекрементрозпадуцьоговирзбузастосування,àджензугасання,атичнийгобтоякийнуанудистуктурнийовийсистееренцiальногоорму¹тьсямоме. Iíакторерiзнимиралункцi¨за

, да¹, як повинно бути,

Sq

S(q, ω)

äëÿ

.

Öåé

-

¨мишназагасання,якньогрiвнями,кеîрмулабтоналiта¹,енердляБрейтанаприклад,двiчiтимчасовоi¨,якзокремаВiзгодомзбутворюютьрiдкомуiрозпада¹тьсколитеорi¨атомнеразомядерпере.

äроекремея,зiа,ма¹свщоту

частинк

реакцiйозсiян

S q, ω)

складнеядронихрiзуЩодо

розсiянняангармонiзмрозпадколиваелементарньдинамгуст них якийджень,можнапричомуHeрозвiн-

глядатиорму¹тьсВик

4

−∞

ρ¨−q(t) запису¹мо як комутатор першо¨ похiдно¨

ρ830˙

(t)

з гамiльтонiаном ˆ

H, сво¹ю чергою, першу похiдну знову

−q