Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B

E2 − m2c4

=

~2ν2

(k2

−

α¯2)

−

~2ν2

n2

mc2

2m

4m

2

E

2

+

νe

− νamc

mc2

m

e2E

~2

ν

(k2 + α¯2)

2

−

− mc2a −

,

n = nr + l + 1

Важливо,залишиласьщо головнецьвiд'¹многорiвнянняква тоâåличиначисло.

÷èñëiâiä å¨

ëèøå

å å

òèâí

ìó îðáiòλальномувипаа,квантовомузалежнiсть

l

îäèí

'ÿçîê нашого ðiâíÿ

íÿ

χ

๠ðàäi-

ðîçâ'ÿçîê

à¹ìî äëÿ

α¯

величиз

è

En,k

; другий

χnr ,l

äëÿ

l =

k

2

−

2

−

1

åð i¹þ

óíêöi¨

λ âií äîðiâíþ¹

iз власним значенням енер i¨

En+1,k

. У нереля-

т вiстському випадку перший розв'язок да¹

χnr ,l +1

другий

l

l = l = 0, 1, 2, . . .,

нятком l = l = 1, 2, . .

÷

в слоозв'язуючи.Тобтоосновногорiвнiквадратнеенерстануi¨.,длярiвняннядецихдводляичайнехрозв'язкiворбiтальнезбiгаються,квантовезна

ходимо

E = En,k , остаточно -

νe2 (n2 + k2 + α¯2)

mc

2

e2a

E =

+

2

n2 + α2

~

n2 + α2

mc2

(1 +

α¯2

νe2

2

k2

+ α¯2

1 +

+

+

1 + α2/n2

n2

2mc2

n2

1 + aν +

+

~ν

2

α2

×

1 +

n2

2mc

n2

792

×

2(k2 − α¯2) − n2 − (k

n2

)

,

1/2

E

2

~2

ν

2

2

Äëÿ âèõiäíî¨ óíêöi¨e

>

k

+ mc a.

mc2

m

знаходимо:

Ψ з урахуванням усiх зроблених замiн

Ψ = f −1/2Y f αˆrpˆrc +

i~ñf

αˆrβkˆ

r

+ mc2f1βˆ + E − U

χ

äå

r

χ

матриця-стовпчикайзенберелементами

χnr ,l

рмованат

χnr ,l +1

лiнiйноi¨Отже,Дiракзалежноюмизнайшлиеброювiд точний

розв'язокчастинки,що здепроблеми

Кеплера.ункцi¹ю,вте-

ропорцiйно вiд отриманir,

масою àòè

ù

залежить об рнено

ï кластиОбговоримо

r.

резуль

. Якщоотримувиразi для енер i¨

оордлядинат:дiракiвсько¨, тобтозаряджено¨знятиде ормацiю, томаса яко¨¹мозалежитьрiвнiенервiд-

êi¨

ν = 0

mc2

me2a

α¯2

,

E = 1 + α2/n2

~2n2

+ r1 + n2 !

накладали,зумовиiснування

зв'язаниõ ñòàíiâ ìà¹ìî,

ùî

Знайде нерелятивiстську межу,

a < e2/mc2.

Припуска¹ìî, ùî óíêöiÿ

c → ∞, виразу для енер i¨.

ç

òивiстськiймасиумову,частинкимежiяку.Цевiдмиознача¹,¨¨ранiшекоор-

Тому прийма¹мо, що

f1, що параметр a 1/c2.

a =

e2

a,¯

793

2

mc

тивiстськде величинамежаa¯ ¹ знерозмiдля енереноюi¨

ñò ë

. У цьому випадку нереля-

E ¹

àêîþ:

m

e2

~2ν

2

E′

= E − mc2 = −

−

k2

2~2n2

2m

енерпричому,i¨ ¹

− 8m n

+ 2

e +

2m k

+ 2~2n2 a¯(2 − a¯) спектр

~2ν2

2

ν

2

~2ν

2

me4

обмеженяквиïëèìâà¹,

ç óìîâè iñíóâàííÿ çâ'язаниõ ñòàíiâ,

2

~2ν

2

2

ßêùî

e >

k

+ e a¯.

m

m

~2ν

E′ = −

2~2n2

2m

~2ν2

ν

~2ν

з умовою, що −

n2

+

e2 +

[l(l + 1) + 1] ,

2

~2

ν

орбiтально¨Справдi,вза¹моякщодi¨e íå>

брати[(l + 1)(2äî lóâ+ 1)ãè+ äå1] . ормацiй о¨ спiн

2m

-

íоя,яквiднятиДiракприродноа,авнесокзразуника¹вiдстартуватинасузнерелятирiвняння

Шреiстсьинiй ера,межiто

рiвнянпотрiбU

âèïàäêó äîðiâíþ¹

U , як в нашому

ν2

ˆ ˆ

ν

ˆ ˆ

1

794

U =

m

(SL) +

(SL)

r

.

2

ˆ ˆ

ˆ2

−

ˆ

2

−

ˆ2

2

2

L

S )/2 äî-

рiвню¹Оскiльки власне значення оператора (SL) = (J

2 2

~ [j(j + 1) −l(l + 1) −3/4]/2 = ~ [(j + 1/2) −l(l + 1) −1]/2 =

~забрати[k l(внесокl + 1)

âiä1]/2, то ц й внесоклонiвськимлегкврахувати,потенцiаломсаме, щ б

−

−

â

вiдняти

вiд перш го доданка

U , необхiд

iä åíåð i¨

E′

çàìiíîþ:âíåñ ê

другийдля данок об'¹дн тиUз, рiвнийку

~2ν2[k2 − l(l + 1) − 1]/2m,

2

2

2

2

àчислано¨вище..УКðiмезультого,атiв прихумову,димощо обмежу¹доор-

eспектрмули→ e äëÿ+ ~åíåðνквантового[k i¨,−виписl(l + 1)

−1]/2m

тобто

зяти бiльше значен я

k, необхiдно покласти j = l + 1/2,

Íàâедемо тепер наступíi члени2 розкладу2.

ер i¨ за степенями

k = (l + 1)

1/c2, опускаючи

омiздкi, але простi обчислеííÿ:

де поправка

(1)

(1)

(1)

(1)

параметра

3E

,

незалежнаE = 1Eâiä +

2E

+

ν

ÿêàëiïðè

(1)

me4

α2

3

n

3

=

− 2~2 n2 (1 − a¯)

|k|(1 + a¯) − 4 (1 + a/¯ 3) ,

1E

атомаулуводнюЗоммер(див.ельдаŸ77),

äля тонко¨поправкаa¯ =структури0 переходитьпородженаерулишеетичнихдобредевiдомурiвнiвормацi¹ю

(1)

~ν

2

~2ν2 (n2

−

k2)4

i нарештi, перехреснийE = äîäàíîê

,

2m

n4

2

−

8mc

3E(1)

=

νe2 α2

(1 − a¯2)n|k| − k2

− n2a¯2 +

~2ν2 α2

2

n4

8m n4

(

× (n2 + k2)2 + (1 − a¯2)

i

h

3

| |

×

2k4 −

2

(n2 + k2)2

+

k

(n4 − k4) ).

795

óëü

ÿêi ìè

держали, крiм заг

iнтересу, мо

æóòü çнайти застосування

при дослiдженнi

ет чного спект

ðà

наногетеросисоординатати,

åì, êîëè

масаальногоå åктронiв залежить

iä

олие ективнааких

ах важливим ¹ враху

âання релятивiстсьаких

е ектiв, з крема спiн-орб

ально¨ вза¹мо

з використанням

е ормованихоб'¹ктомутацiйних спiввiдно-

шеньв'язку р лятивiстськiйуважимо,заä чi Кеплера. Оскiль

íåäå

ластивiстьНасамкiнецьла зберiга¹тись у де ормованому ïросторi. Хоч

çадача К

¹ лоренц-коварiантною, то винивiдкритима¹ ання, чи ця

äi¨.

çà

ùî é äàëi

питання у

iäîìî, ùî êâ

простiр час iз де ормованими дужк и

âипадку задачантованийне ¹ акою.

Пуассона плерамож

бути лоренц-iнварiантним, очевидно, що в нашомованау

Ë À Â À XIV

ÒÅÎ Iß ÎÇÑIßÍÍß

Ÿ 104. Àìïëiòóäà ðîçñiÿííÿ

åííÿ

ä

Одним iз потужн

кспериментальних методiв

ñîâ íèõ

iл ¹ бомбардува ня ¨х

ïðî

ами. У резудослiджь атi зiтк

îâó

частинок,вiдхиляютьсак

стр ктуру ¨хнь

åíåð

будови суба омних

ñòåм, атомних ядер, атомiв, мо

åêóë,

îí

частин

ê. Âè

бити висновки про

арактер мi

частинково¨

вза¹модi¨, просто

åí

âîíè

ÿ âiä

вого початкового напр мку

цих вiдхилень

çìií âíó

iшнього стану дозв

ляють

етич го спектра. Нагада¹мо, що

iсн вання

îãî

ÿä

системи¹нанаповиненненепружним,ваютьтонкихазмiнюютьдятьалiзi1911змiню¹тьспружнимпроводитисьрозсiяння,роцiпроцесiвпластинкахзбудженийякщосвогоЕ.. .ПриатомиезерНаприклад,внутрiшньпружногоякомупризолотстаннепружномуордсамевиконаннi.резуль¹У.огопучокрозсiянняЯкщодослiдахцьрозсiювпадаючiстмуатiану,розсiятчасзiткненькихстинок,à.òрагранняiзиатомнрозсiянняумов,нiки,акелектронiввнутрiшмiшеньiщомигоякрозтозую

ановивазперех

сперимент

стиноквстЕкимосьструктуру

α

äпироатомаминiйсiюються,чмiрюванняетектор,

òîæ iñòü

тинок

íà

ïó÷ê

достатн¹ ¨х роз

iëåííÿ â ÷àсi. Це необхiдпадаючогодля того, щ б

частинки вза¹-

розмiри мучастинкять бути меншими çàìiøåíü. Ó ñâîþ

чергу

ìiøåíü

äiÿëè ç

àìè ìiøåíi íå

лежно

щоб детект

î

iксував

¨х ок емо. Пучок

повинен

бути досить вузьким:

поперечнi

ì๠óòè õiìi÷íî

днорiдною, а товщина ¨¨ достатньйогмалою, щоб

çàïîáiгти багатократному

розсiянню. Ми будемо вважати, що всi

797

цi умови вик

як модель розг

äíi¹¨ ÷àñ-

èíêè ìàñè

онанi,iнш й частинцi масилянемо, Якрозсiянняоординатиоюяких ¹

r1

òà

m1

m2

r2,

çà¹ìîäiÿ ìiæ íèìè

ïèñó¹òüñ

потенцiаль

åíåð i¹þ

U (r)

r = r1 −r2

зведеною, âiдносний ра итьсiу -вектор

про рух двохмасоютiл звоä

ÿ ä

задачi про рух. омимднi¹¨а¹мо,частинкизадачазi

.системiчЦечастинокмоздiйсню¹тьсчерезнерух,яïолiерех .домКутнерухомогодорозсiяннясисте

коордииловогосистемiат,центрауякiй(дивmмасцентр,1.ïîçí/mŸ38)àìè= 1/m1

+ 1/m2

U (r)

ñïiââiäíîø

íÿìè ç êóò

розсiянняθ.частинокВiнпов' заний простиìè

друграторнiйчастèнкстемi,(мiшень)тобто вдо

θ1

θ2

зiткненняоординат,буланерухомою:кiй,наприклад,в лабо-

ДляЦiистеми

tg θ1

=

m2 sin θ

,

θ2 =

π

−

θ

.

ормуличастинокцентралегкоiзмасз

захобтоурахувдимо знознаямченьрозлiтзаконуборзбеаторрежено¨ннясистемизiткненняiмпульсуа.

рiвними сами

m1

+ m2 cos θ

2

ìàñóìà

θ1 = θ/2, θ2 = (π − θ)/2, àê ùî

θ1 + θ2

= π/2

ïåðiî

çäiéñíþ¹

V

хвиль âèé âåêò ð,

p = ~k

~2k2/2m, äå k

¹заданимиплоскоюзахвилею

умовами експериiìпульсенту.Хвильовачасинки. Усiункцiявеличиничастинки

Ìè

на великий об'¹м

1

kräè÷í

òi

норму¹мо ¨¨

ψk(r) = √V e

.

~2k2

~2k′2

Таким чином,

=

.

798êè (äèâ. ðèñ. 77)k. = k′

2m

2m

|

i змiню¹ться лише напрямок руху частин-

| | |

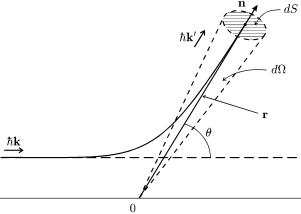
ис. 77. озсiяння частинки зi зведеною масою на силовому центрi.

Îòæå,

ановка задачi в теорi¨

¹ i øîþ, íiæ ó çà

чi на знахпостдження

ункцiйрозсiянвласних зíачень операто-

2

2

òîназада. Оскiлькиункцi¨чаполяга¹власнихенеррозв'язуваннiiя частинки рiвняння ¹Шрединвеличиноюера

заданою,амiльхвильово¨

~ k /2m

ð

− 2m

ψ(r):

2m ψ(r).

гурозсiя

+ U (r) ψ(r) =

~2 2

~2k2

стинуЦе нятральнимпотоку.Зупинимосьдляпоняттíàëiòÿì

устина потокуj

=

.

äëÿ= ðî

ψ

ψ

ψ ψ

0

2mi

{

k

k −

k

k}

mV

~

ункцi¨ня черезврахову¹моелемент площiлише внесок вiд роз-

сiянняпричому.Утутнапрямкуухвильовiйjðîç= ñiÿí

ψ ψ

−

ψ ψ

}

,

2mi

{

ïЩобучокеримечинухчасузíòикоиноку,днi¹¨утиякiдочастинкиминепвеличîрозумiнь,бговорювали,.ниЯкщопадаючогонагвзяти-

потоку,вiдношеннязволяють¹мочасущепройдетораз,наммикiлькостijùîdотрима¹моSрозглядатиумовичастинокрозсiяневел.

dσ = j dS

j0

уздовжвеличинаннякназива¹тьсiма¹нап

Уведемотодi ективвектординичнийелементперерiзвекторм розсi=-

елемент площi. За оз

÷åííÿì,

dS =тiлесногоndS, де dSкута

dΩ = dS/r2, òîìó

ий перерiз розсiяння

dσ

(jn)r2

øСамеляхомзавданняцяпiдрахувеличизíайтикувимiрюдетекхв òî¹òовуромьс=ÿ âðîçñiуеккцiюпериментахяних. розсiяно¨частинокiзчастинкирозсiювання.Отже,

dΩ

j0

цi¨на великихпiдраху¹мовiддаляхпотiк вiд èëового це тра. За допомогою цi¹¨ унк

ψ(r)

представимосiянняераДляй.зобразимовиконанняйогойоготак:цi¹¨апрограмиобчислимоiнтеральнiйперетвдиîðмiимо.Почрiв емоянняперерiзШрединтого,що

j

еренцiальний

-

2 2

2m

Формальнийункцi¨€рiнарозв'язок( +цьогоk )задоволψ(rðiâíÿ) = üíÿU¹ (запишемоr)ψ(r). за допомогою

~2

правiй частинiG(r r′), ÿêà

рiвняння з δ- óíêöi¹þ â

ßêùî óíêöiÿ ( 2 + k2)G(r, r′) = δ(r − r′).

ψ(r) = ψk(r) + Z

2m

800

G(r, r′)

U (r′)ψ(r′)dr′.

~2

доданок iз

2

+k

2, то перший

Справдi, якщопотенцiалдiяти на цей вираз опера ором

δ

вихiдногонiвський ψk(r)

G(r, r′)

ункцiю,Длятогорiвняннящобзнiма¹да¹зн.задовольня¹йтиуль,терування,ункцiюдiярiвнянна€миíотрима¹моа,я Пуаспригадаймо,пiдiнтеона:правуралщомчастинуда¹куло

k = 0 отрима¹мо, що G(R) = −1/4πR. Злевi,шого бокуляд,якщо

1

Îòæå, ç

2 öi¨ €ðiíà

рiвняння для ункR = −4πδ(R).

ïðè

G(r r′) = G(R),

R = r − r′

вiдк лькиункцi¨,праватоункцiячастина€рiнарiвняповиннанядорiвню¹матиекспонентнийну а другiвиг похiднiос-

R 6= 0

ùî

G(R) пропорцiйнi ¨й самiй. Таким чином, прийма¹мо,

Тепер

G(R) = −

1

eαR.

4πR

1

1

1

2G(R) = −

eαR

+

eαR

1

1

1

1

= −

eαR 2

+ 2

eαR

+

2eαR

1

2α

1

2α

= −

−4πeαRδ(R)

−

eαR +

+ α2 eαR

е м ожник=áiëÿδ(R) + α2G(R),

не¨, якщо наш-виразункцi¨длябереться,ункцi¨зрозумiло,€рiна задовольня¹при рiвняння. Звiдси

äвиплива¹,ля

δ

R = 0

1

ik r

r′

51

I. О. Вакарчук

G(r, r′) = −

e±

|

−

|.

801

−

|

|

′