
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf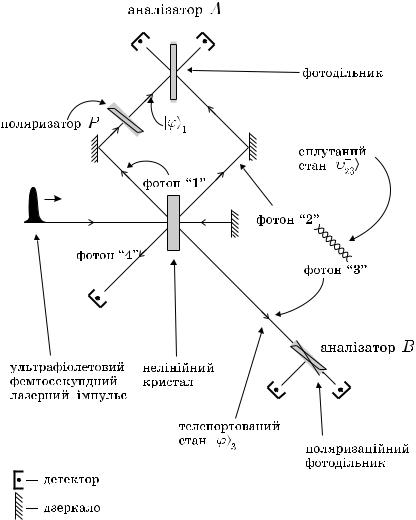
èñ. 74. Схема Iнсбрукського експерименту з квантово¨ телепортацi¨.
742
тобто вiдбува¹тьс |
процес |
|
|
|
ного випромiнювання. Один |
|||||||||
ç îòîíiâ |
|
|
|
вер икально, |
iнший горизонтально. |
|||||||||
Народженi отони поширююдвоьсотомежах поверхонь двох конусiв |
||||||||||||||
âèзначено¨ |
поляризацi¨: |
âîíè |
переб |
ватимуть суперпозицiйно |
||||||||||
промi ю анн , у к жному з |
ÿêèõ |
|
мають пев |
íå |
поляриза |
|||||||||
öiþ |
5 |
. Íà ä |
õ ëiíiÿõ |
|
|
|
|
цих квонисiв отони |
|
|||||
|
|
|
|
|
еретинуклад, звичайними поворот |
|
крист ла |
|||||||
у ст нi. Причому, |
|
|
||||||||||||
зацiй их станiв. Позначимо |
цi тони номерами 2 амит матимуть. О же, |
|||||||||||||
æíà |
приготувати ант симетричну суперпозицiю ¨хнiх поляри- |
|||||||||||||
ìиотонiвма¹мо сплутполяризованийст Ψ− |
, тобто приготували EPR 2 3 -пару |
|||||||||||||
|
|
|
. |
P |
|
пiдтвер |
|ϕi |
|
|
|
||||
|
|
|
|
|
|
| |
23 |
|
|
|
|
|
|
|
àíàëiçотонПерехми димо1B.анарештi2 . В |
äî |
налiзу резульсклада¹тьсатiввимiрювання над |
||||||||||||
ПоляризаторпрохтораФотондить.Вiдбитак2 iзьпiсляквiдвiдбивсталдзеркàпороннялачастинаджу¹,вiддзеркаладвапервинногоiншiруха¹тьсяотониiмпульсудоДетектор1аналiзазнову4 -. |
||||||||||||||
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
акiксу¹Отждоотонаналi4атораðèцимготовля¹ |
|
àí |
щодлятовленоот отона1 був1 .вiдiсланий |
|||||||||||
|
|
|
е, у д який моментA. |
|
|
|
|
|
|
êðiçü |
||||
|
|
|
÷àñó ïðèã |
початковий ст |
||||||||||
|ψ123 |
системи з трь х частинок, а саме: з от на 1 у станi |ϕ |
|||||||||
|
|
н правлено¹тьсяотонак дож доаналiзатора , отона 2 з EPR 2 3 -пари, |
||||||||
биваючогщоякийрух |
|
|
|
|
A |
|
|
|
||
|
|
òîðà |
аналiзаторiA 3 -го отона з цi¹¨ пари на шляху до |
|||||||
|
|
|
|
|
|
|
|
|
|
- |
пройшла,дзеркалоокалоерпозицiйнЯкщоемийженiстьдобуткдновiснихдваабодзеркала,тер.зiмуПовнавiдбитисьдентичнiсвогома¹станiеруютьпросторово¨хвильовап'ятдесятбоку,.вiдбув.iОтже,симетричноюотони¹тьсявiдбкожвдарятьункцiячастинип'ятдесятрозщеплення,якийсамимчастинаiззвичайнаотонiвуотонiвтойутрачаютьспiновушансiвсамийпроменяякпроменiперебува¹бозепройти,часполяризованаòановокобтозсв-частинокнапiввйоб:юкожена,дзерiндищосу- |
||||||||||
ризацiйнудорiвню¹вiдуаль |
|
|
|
|
A |
|
|
|
||
5 |
|
, |
повинна бути |
|
|
|
|
щодо ¨х перес |
. |
|
|
В оптично |
êð |
|
|
àõ |
ак звана |
|
хвиля |
|
|
звичайна хвиля поляризована |
|
|
|
|
||||||
паралельно до головного перерiзу. В достатнь |
||||||||||
перпендикулярно до площини го |
|
ого перерiзу (тоб |
площини, як про |
|||||||
òîвстих кристалах звичайна й незвичайна хвилi ¹ просторово роздiленими. |
||||||||||
х дить че ез лiнiю напрямку |
ðîìå |
я i оптичну вiсь кристала), |
iíøà íå- |
|||||||
|
|
|
|
|
|
|
|
|
|
743 |
|
Два отони залишають дзерк |
|
дному напрямку |
äíî |
||||||||||||||||||||
но зСправинципдвами |
|
|
|
|
|
мех нiки,iмовiрностiописуватисьроб ак: |
åðåìî ó |
ó |
||||||||||||||||
му пучку), якщо ¨х прост рова х ильова ункцiя ¹ симетричною, |
||||||||||||||||||||||||
ною частиíîþ ï |
|
òîð |
|
|
õâèëповиннi¨ óíêöi¨. |
|
î¨ ïî i¨, çãiä |
|||||||||||||||||
обидва вiдб |
|
|
|
ютьспотрапляють. А пi |
|
|
|
|
||||||||||||||||
áòî âîíè |
|
бидва |
|
|
è, |
íè |
|
алодин iз детекторiв. Щоб п(отра |
||||||||||||||||
ïèòè |
ðiç |
|
|
детек |
|
|
|
|
|
|
|
антисиметрич |
||||||||||||
à |
|
|
i, |
|
|
|
|
|
квантово¨i рахунокбира¹ щодатково¨ ази стос |
|
íî |
àì- |
||||||||||||
|
|
|
отони |
ïðî |
|
|
|
дночасно |
çíi |
|
|
|
|
ÿê |
||||||||||
ùî âîíè îá |
|
|
|
|
àáî |
ÿòü êðiçü |
напiвпрозоре детектори,дз ало, |
àáî |
||||||||||||||||
росто ових амплiту |
|
|
öèõ äâî àëü |
|
ïîäié |
ïiäíîñ |
||||||||||||||||||
¨¨ модуль до |
квадрат |
. Наг да¹мо,тернативнихпр вiдбиваннi |
àìïë òó |
|||||||||||||||||||||
хвильелектромагнiтно¨ункцi¨ можна зробити |
|
|
|
|
пiдбором цi |
|||||||||||||||||||
ëiòóäè õâèëi, ÿê |
пройшла |
êðiçü |
äзеркало. Iнш ми слîâàìè, |
|
||||||||||||||||||||
ä ÿê |
àçà . |
|
|
|
|
|
хвильово¨ ункцi¨ отона при цьому набiга¹ |
|||||||||||||||||
ïросторово¨ частини |
||||||||||||||||||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
сплутаного |
àíó äâîõ îòîíiâ, êîëè ¨õ |
||||||||||
|
Îòæå, ïðè |
|
|
|
|
|
|
|||||||||||||||||
ðå¹струють дночасноутвореннi |
рiзних детексторах, |
|
|
|
части |
ó |
||||||||||||||||||
¹¨ ази. Тобто |
àìïëiòó |
друго¨ подi¨ (мова |
просторовуйде вiдбиван |
ÿ |
||||||||||||||||||||
îòîíiâ) дода¹ться зi знда ом мiнус, якщо азу пiдiбрати |
ðiâíîþ |
|||||||||||||||||||||||
вониоскiлькиженнячастинаπ. ю,Колипотрапляютьтосиметричностiмуситьзрпростороваакзумiло,хвильбутищооварiзнiчакповно¨стинаотонижункцiядетекториантисиметричною,хвильово¨хвильово¨непростоантисиметричноюможуть.Уцьотонибудеомуункцi¨брiвнавиптобто¨¨¹поляризацiйнадкунудномудорiвнюватитисиметричлевi,дляпучку,зберетому-
хвильовий вектор част ки, |
|
|
|
, |
|
içü |
|||
|Ψ12− i |
|
|
|
|
|
дночасно1 2 (схемаперебуваувi |
|||
ютьмкнутТому. сплутаномунаякщозбiжнiсть),дваантисиметдетедетекторимизна¹мспрацьаналiзаторiмущоовуютьстнi |
|
|
|
|
|||||
|
|
частинк |
|
|Ψ12− i |
|
|
|
||
гою, говорить про те, що |
|
|
3 перебува¹. Ау це,станiсво¹ю чер |
||||||
Тобто, як тiл ки два |
довжи |
|
|
|
(−)|ϕ 3. |
||||
|
|
|
|
|
|
|
|
|
- |
|
àно¹стосовноотонаŸ25при¹вiдбито¨напiпрохпрозоредженнiхвилiдорiвню¹частинкизеркдаткало),о¨крiзьхвиля,азипотенспра( щоöпройшлаiальнийювалибар'¹ратонкдно |
||||||||
бар'¹(яким6Як'¹ра,тутнабувпоаздля |
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
π/2 − ka) k = 2π/λ |
|||
вибратиãî |
рiвноюa → 03/4,цядовждатк |
|
λ |
|
хвилi. Наприклад, для дорiв |
||||
|
õâèëi,ààçà |
|
π/2 якщо ширину |
|
|||||
|
èí |
|
|
|
|
|
|
|
|
íþâ |
(−π). |
|
a = 3λ/4 |
то додаткова аза ма¹ |
- |
||||
744 |
|
|
|
|
|
|
|
|
|

часн , можна звiдси перед в ти класичним ка алом iн ормацiю7 |
|||||||||||||||||
à Традицiйними |
поляризацi¹ю |
|
|
|
|
|
|
|
|
|
|
||||||
тинкудо î÷êè B ïðî òå, ùî â àналiзаторi B повинен виявитись стан |
|||||||||||||||||
(−)|ϕ . Тим самим, ченостiан|ϕ |
A |
|
B |
! |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
îãî лiтературi,ова хвильоваякi об i- |
|||||
нюютьс7 станiя iнз 45орм-ноюцi¹юперсонажамимiжпунктв миангломовнiй8, тобтонаукй |
початкностинкиполяризатором1 на час- |
||||||||||||||||
P Нехай3 .для◦ |
визна |
|
|
телепортованоотон1 приг тз чвiй |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
! |
|
|
|
|
|
|
|
|
|
|
|
! |
|
! |
|
|
|
|
|
|
|
|
||||
|
поляризатора. |
çàäà¹мо матрицею, ¹ пiдлiтки: Алiса з Амстердама |
|||||||||||||||
Боб8ДiюiзтакогоБостон |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
ˆâ ïîëÿðизатор у станi |
|
|
|
|
|
||||||||
Отже, якщо отон потрапля¹Pπ/4 = |
2 |
1 |
1 . |
|
|
! |
|
|
|
||||||||
|
|
|
|
|
|
|
! |
|
! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| li, то пiсля цього ма¹мо: |
||||
Тобтоˆ |
1 |
1 |
1 |
0 |
|
1 |
1 |
|
1 |
|
|
|
1 |
|
|||
ìè îòðèìó¹ìî ñòàí iç |
поляри= ç2àöi¹þ â 45= 2 |
| li + | ↔i |
= √ | i. |
||||||||||||||
Pπ/ |
| li = 2 |
1 |
1 |
||||||||||||||
|
|
1 |
|
|
1 |
|
|
|
|
|
|
2 |
|
||||
хвилiпада¹ дорiвню¹хвиляполяризацiйномулишеполовинiпадаючогостанiв45 потоку◦, .однакЯкщовеличинацейполяризаторпотокуцi¹¨
|
|
|
|
|
|
|
|
|
|
◦, |
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
1 |
|
1 |
1 |
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
Тобто 45 |
Pπ/4 |
| i = |
√ |
|
1 |
1 |
1 |
= |
√ |
|
|
|
1 |
= |
|
| i. |
|||||
|
|
|
|
2 |
2 |
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
-ñòàí |
|
|
|
|
|
|
! |
|
|
|
|
|
|
! |
|
|
|
|
|
|
◦ |
|
| i |
|
|
|
|
|
|
|
|
|
Pπ/4 |
|
|
|
|
|
|||
утратПоляризатор,. налаштований нà ñòàí |
|
|
|
|
|
|
, i хвиля проходить без |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
◦ |
, зада¹мо матрицею |
|||||||||
|
|
|
|
|
|
|
|
|
|
(−45 ) |
|
! |
|
|
|
|
|
|
|
||
Легканомпереконатись, що Pˆ−π/4 |
= 21 |
1 |
−1 . |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
−1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
◦ |
-ñòàí |
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
(−45 ) |
|
| i = (| ↔i − | li) / 2 |
|
||||||||||||
ñò |
. Матрицi вертикального |
а горизонтального поляризаторiв¹ йоготакi:власним |
|||||||||||||||||||
òàê ùî |
|
|
ˆ |
= |
1 |
0 |
ˆ |
= |
|
0 |
|
0 |
|
, |
|
|
|
|
|||
|
|
Pl |
0 |
0 |
, P↔ |
|
0 |
|
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ˆ |
|
|
, àëå |
ˆ |
|
; аналогiчно |
ˆ |
|
|
|
, ˆ |
745. |
||||||||
|
Pl| li = | li |
|
|
Pl| ↔i |
= 0 |
|
|
|
P↔| li = 0 P↔| ↔i = | ↔i |
||||||||||||
óíêöiÿ |
поляризацi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
− |
|
|
◦детектори-стан, бто на виявлення стану |
ϕ |
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
öi¨ |
|
|
|||
поляризацiДляаштованианалiзу ϕ |
= |
| i |
|
| i |
= √ |
( |
|
+ |
|
|
) . |
|
|
|
|
|
|
|||
|
| |
|
|
|
|
2 | li |
|
| ↔i |
|
|
|
|
|
|
||||||
|
éненадзеркало45 |
ногоздвомастаíóдетекторамиотона 3 вик.Одинористовувалосьiзнихна |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
òîãî, |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
налiзаторi-стан. Якщо| |
|
спрацювумови,iнший |
||||||||||
аналiзаторiдночасноперпендикудвалярний |
ньогоСправдi,( 45◦) |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
− |
|
детекторiв45 |
-детектор |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
◦ |
|
|
|
|
|
|
1/4,B то промовчавжнаорити |
про тел портац ю за |
|
ùî |
||||||||||||||||
(íiñòü45◦)-дночасногодетектор спрацьовування. двохпри |
телепорт аналiзатоIмовiрнiстьйм |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
A ä ðiâíþ¹ |
оскiльки при цьому реалiзу¹ться ст н Ψ− |
äèí |
||||||||||||||||||
ч тирь х базисних ст |
дорiвню¹Белла |
|
|
|
|
|
|
|
|
|
|
12 |
|
|
||||||
спрацювання в цей момедетектор (Ψ12− , Ψ12+ |
Φ12− , Φ12). |
|
|
B |
|
|||||||||||||||
|
|
|
|
|
(45◦) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
приню¹заговортелепортдиницi,ятьстимо,ацi¨дночасно,отже, í ймовiрнiсть-детектора1/4.Приспрацьщоаналомуцзтриважливо,торiдетекторидорiвщо- |
||||||||||||||||||||
лiзатораПри у |
|
ùî( 45◦)òîíè- |
|
нау B2 невдарят ов ¹дзеркало. ана |
||||||||||||||||
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
робити, затримавшиA íåî |
|
1 вонийогоне шляхуiнтер еруютьдо |
. Öå ëåãê |
|
||||||||||||||||
отонтобто |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||
поло.жТепереннядзеркала,iмовiрнiстьщоднвiдбива¹часногопервiснийспрацювання,емтосенаприобохунла |
||||||||||||||||||||
текторiвниймiнiмпульсю |
|
ëåâi) |
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|ϕi ç |
- |
||||
éìîâiðíiñòüвiдби аютьсдорiвню¹працьвiдовуваннядзеркдвомала,шансаманалiзаторiкабожногообидватирьдетектпройшлих:овуванняобидварiвкрiзь ньогони. |
||||||||||||||||||||
Ààáî |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
детектню¹ 1/2. Так(двохщо вймовiрнiсть, |
дночасн |
|
|
ñ |
|
ðàöü |
|
|
|
B äîðiâðüõ |
||||||||||
спрто ма¹моцьдорiвню¹ |
|
A |
|
îãî |
щоB) дорiвню¹прителе 2орт/4 Чацi¨,1/2якщо=днак1/4.òеперТоб |
|||||||||||||||
овуiлькiстьтусаму |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
тичнозатримки |
( |
45◦ |
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
||
− |
|
спрацювань-де ектор |
|
умiтелепортацiю-цi¹¨детекторазалежностiзалежноану(якийвiдеоре- |
||||||||||||||||
õóâ òè |
|
|
|
|
|
|
|
|
|
|
. Îòæ |
|
|
|
|
пiдчасу |
||||
|
отонану 1 , |
матимемiнi(ì45◦) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точки
A746мивиниклаомп'ютеримашинамиТеорiяточку квантовB.виявляютьперетпринциповiŸ нiх96комп'ютерiв.квантово¨порiвняноКвантовийперевагиiзикизавдякимiждисциплiнарнакласичнимиомп'ютерматематикивикористобчислювальнианню. Кванука,суòùîîâiò¹
во квантових |
. Òàê |
наука, як криптогр iя, т ж знай |
||||
шла новий розве ектiвк, оск льки тех |
iчнi засоби з хисту |
|||||
пря пов'язанi з можливостями |
|
|
ашин,ормацi¨крiм |
|||
òîãî, íîâi ìî |
дають i принципи |
ìåõàíiêè. Òîð |
||||
чення дiльна0 1, ма¹ |
назву бiт . Квантовiобчислювальнихсистем з двома станами |
|||||
Íåïî |
жливостiди иця кл сично¨ |
зацiкормацi¨, що набува¹ два зна- |
||||
кнемось |
тут цих питань з |
метою |
|
авитиквантово¨Ч ча. |
||
називають квантовими бiтами (qubits), скорочено кубiтами або |
||||||
квабiтами, базисом яких ¹: |
|
|
|
|
||
|
|
нормованi |
= |
1 |
, |
|
|
|
0 |
≡ | ↑i |
|||
|
|
| |
|
0 |
|
|
справуй |
|
1 |
|
= |
0 |
. |
|
|
| |
≡ | ↓i |
|
1 |
|
Тгiльбертовогомобiльше)бтоВiзьмемослугувати.квабiт.Зприкладамидобутокж просторуямийбудьце-як. Вiнквантоваакихмождвохнасистемзображсистема,диницюквабiтiв:миатижвекториякчисланеодноразовома¹0двадвовимiрного1.станиКвабiтоммали(
|
|
0 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|00i = |0i|0i = |
|
0 |
|
, |
|01i = |0i|1i = |
0 |
|
, |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вимiрному гiльбертов |
|
|
|
|||
|
0 |
|
|
|
|
0 |
|
||
якийОтже,можемиотриму¹мо|10зображатиi = |1i|0i = |
|
0 |
|
, |
|11 = |1i|1 = |
|
0 |
. |
|
1 |
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
базисчислаувiд4- 0 до 3. Прямий добутокму просторi, |
|||||||||
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N êâàáiòiâ747

|
квантовi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
цiлiочевидночислаутворю¹вiд 0 добазис, вектор x у якому дозволя¹ зображати всi |
||||||||||||||||||||||||||
|
|
|
2N − 1 (N квабiтовий ре iстр): |
|
||||||||||||||||||||||
|
|
|
|
|x = |xN −1xN −2 . . . x2x x0i, |
|
|
||||||||||||||||||||
унiтпiдзм нюютьнаарнимо |
|
|
|
xj |
= (0, 1), |
j = 0, . . . , N − 1. |
|
|||||||||||||||||||
çгляньмовоюстаниоператоромквантовийкремомп'ютер(дивгологiчнiквабiт.приклад. елементПеретвi з3 якдоèренняŸ13)х, тобтосклада¹тьсяАдамараоператори,зада¹ммашинащо |
||||||||||||||||||||||||||
|
|
|
|
|
стануH = ëåã√ |
1 |
|
1 |
, |
|
|
|
|
|
||||||||||||
дiю якого на вектор |
|
|
|
ˆ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
ко знаходимо |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
−1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Hˆ 0 = √ |
|
|
|
|
|
|
= |
√ |
( 0 + 1 ), |
||||||||||||||||
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|||||
|
| i |
|
|
|
|
1 |
−1 |
|
|
|
|
|
|
|
|
|
| i |
| i |
||||||||
|
|
2 |
|
0 |
|
|
|
2 |
|
|||||||||||||||||
|
H 1 = √ |
|
|
|
|
|
|
= |
√ |
( 0 |
1 ). |
|||||||||||||||
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|||||
муТобтовипадкуцейоператорˆзапису¹ìî |
творитьак: суперпозицiйнi сòàни, що в загально- |
|||||||||||||||||||||||||
|
| i |
|
2 |
|
1 |
−1 |
|
1 |
|
|
|
|
2 |
|
| i − | i |
|||||||||||
тового ре iстра, |
|
складеногоN оператз îðiâ |
|
|
|
|
|
|
HN íà |
àí |xi êâàí- |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
ˆ |
|
1 |
|
|
|
|
N двостàнових пiдсистем, ¹ такою: |
||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
1 |
|
|
|
|
iπx |
|1i) |
|||||||
|
H|xi = √ |
|
(|0 + (−) |
|
|1i) = √ (|0 + e |
|||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
1 |
yX |
|
eiπxy |
y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Дiя прямого=äî√áóòêó |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
=0,1 |
|
| |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Àä ìàðà ˆ |
|
|
||||||||
|
|
|
|
|
|
ˆ |
|
|
|
|
1 |
|
|
X |
iπxy |
|yi, |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
748 |
|
|
|
|
HN |xi = 2N/2 |
|
e |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
N −1 |
|
|
|
|
|
|
|
|
|
|
|
X |
HN íà ñòàí |
x |
|
äèòü |
|||
|
|
xy = |
xj yj , |
íiâ, |
|
|
|
|
перево |
||
йогоперевагстн, що ¹ суперпозицi¹ю 2 |
|
|
|
|
|||||||
|
|
|
|
j=0 |
|
|
|
|
|
|
|
à |
|
yj = (0, 1), |
X |
|
|
|
|
|
|
||
|
|
X |
|
X |
|
|
|
äiþòü |
|
||
|
|
|
омп'ютер,щозмiню¹тьсзадиножнекрокN |
|
|
||||||
Т ким чином, дiя операт≡омп'ютераАдамара. . . |
|
. |
|
|
|
|
|
||||
|
|
y |
|
y0=0,1 yN −1=0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
ча¹ натуральне число |
бластi вiдN ст0 докласичним,iоженз| |
яких визна |
|||||||||
|
квантовогой ст жензада¹кйого станнадзада¹N |
ше. однеЦеаджнайголовнiчисло,клу- |
|||||||||
квасичша íтовомукомп'ютерi |
|
|
2 |
|
− 1 |
|
|
|
|
||
|
ннiсуперпозицi¨тостаниецальнопочаткпiдiбранiовасуперпозицiячиселлазернi.Напрiмпульклад,чиселякщо квабiтина ¨хнi |
||||||||||
електрцезна оми, |
|
|
2N |
|
|
|
|
|
|
|
|
доперацiюiншча¹,¨щонадквантовий |
|
|
|
2 |
|
вхiднепроводитьеволюцiонучисло.днуЦе¹ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
зультатi на крок,вихNдi ма¹мознимиобчисленнясувхiднивеликийöiþ÷è ëàìè |
паралельно, |
ðå |
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
ний комп'юквантовийер |
|
|
властивiстьпроводитиN нових чиселза. Класич |
||||||||
àáî çà |
äèí |
àëå íà |
|
|
2 |
|
|
|
|
2N êðîêiâ |
|
|
|
|
|
|
|
|
|||||
|
квантовийективнiстьщединпам'ятiомп'ютерунiтарнийпаралелiзм,. . Ця аралельнода¹операторсамепрацюючихвонаквантовоговиграшвизнача¹яккомп'ютерахчасукйогообчисак-. |
||||||||||
званума¹лень,Отже,Уведемоназвутакнадеоб'¹му |
|
2N |
|
|
|
|
|
|
|
|
|
ратор,для того,тобтщîбквантовийсконструюватилогiчнийдовiльнийелемент,унiтоператорiв Hùî äi¹Φ(íàϕквантовий) диндостатньоквабiтопе749.- |
|||||
який назива¹ться операторомˆ |
|
1 |
0 |
|
|
|
змiни ази. Очевидно |
||||
|
|
0 |
e |
|
|
Φ(ϕ) = |
|
iϕ |
, |
||
ˆ |
iϕx |
|x , |
x = (0, 1). |
||
Виявля¹ться, щоΦ(öèõϕ)|xiäâîõ= e |
|
||||
ˆ арнийтˆ
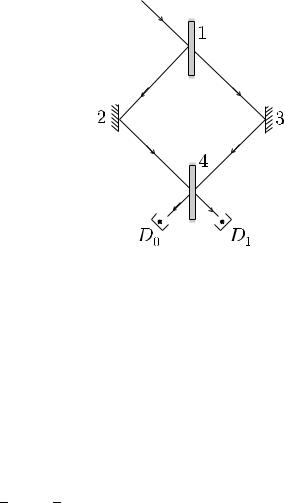
тонкНаведемок напiвпосрiбленезваний iнтерçàðнапiвпрозорийе ñòèéметралодноквабiтовийМаха Цандера (дивквантовий. ðèñ. 75)пристрiй. Отже, нех й ми ма¹мо бар'¹р для ч стинок, це може бути
äçåðê 1, íà ÿê ï ä๠îòîí.
ис. 75. Iнтер ерометр Маха Цандеðà. 1,4 дiльники частинок у вiд-
ношеннi 50/50; 2,3 дзеркала; D , D
оскiлькидетерощепленогоВiдбиваючисьторидзеркалi4вихiдногозвичайних.вiдОбчислимодвопучкймовiрностiленомув 0 зновупотрапляння1 плоскихдетекторидя дзеркьсаплянчастичастинокл я2апiчастинки. посрiб3,пуч
òîð |
частинкправому |
D1. Àìïëiòóäà |
|
|
|
|
|
|
|
íêè |
детек |
|
|
D0 |
|
|
|
|
|
|
|
|
|||||
|
поймовiрнiсть,двiчiшляхувiчiпрохдорiвню¹набува¹дитьвiдбива¹тьскрiа √ |
|
|
iπ/2 |
|
√ |
iπ |
|
|
||||
þþ÷è |
|
|
|
iπ/2 |
|
|
|
|
|
|
|
||
D0 |
|
|
e |
|
/ |
2 |
|
×e |
/ |
2 = e |
|
/2 |
|
|
|
|
|
çу бар'¹р, щоразу уполови |
|||||||||
|
|
Повнапотрапляннялише час яинкивiд(дивдзерк.цейŸ25ал,детекторадорiвню¹виноскупо |
|||||||||||
íлiвомуа сторшляху.744). Амплiтуоливон |
|
|
π/2 |
|
|
|
|
|
|
||||
√√
1/ 2 × 1/ |
2 = 1/2 |
äîðiâíþ¹ ñóìi àìïëiòó ïî D0 |
|
|
. |
амплiтуда потра яння в |
правому, згiднй |
750з принципом суперпозицi¨, |
|
||
лiвому шляхах:
|
|
|
|
|
|
|
|
|
|
|
|
eiπ |
1 |
|
|
|
|
|
||
i, отже, частинка |
|
|
|
|
|
|
|
íå |
потрапиòь у детектор |
|
|
|||||||||
|
|
|
íiêîëèA0 = |
2 |
+ 2 |
|
= 0, |
|
|
|||||||||||
обчислю¹мо й |
|
|
плiтуду потрапляння |
|
D0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
частинкиповнадетектор.Аналогiчно |
||
О е, по першоì |
|
правому шляху амп iтуда потрапляння вD1. |
||||||||||||||||||
äîðiâíþ¹ |
√ |
|
|
|
|
√ |
|
|
|
|
|
iπ/2 |
|
|
|
|
|
|
|
D1 |
ëiòóäó, ðiâíóiπ/2 |
|
|
|
|
|
|
|
|
|
; |
|
|
ëiвому шляху м ¹мо амп- |
|||||||
e |
/ |
2 × 1/ 2 = e |
/2 |
|
|
|
|
|
||||||||||||
|
√ |
|
|
|
|
|
√ |
|
|
iπ/2 |
|
. Òàê, ùî |
àìïëiòóäà |
|||||||
ймовiрностi потрапитиiπ/2 |
|
|
|
|
|
/2 |
||||||||||||||
1/ |
2 |
× e |
|
|
/ 2 = e |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
D1 äîðiâíþ¹ |
|
|
|
||||||||||
à éì âiðíiñòü |
|
|
|
|
A1 = |
|
1 e |
2 + |
|
1 e |
2 = e 2 , |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
iπ |
|
|
iπ |
iπ |
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
||
тектор |
|A1|2 отрима¹мо= 1, то частинка завжди потрапля¹дноквабiтовимде- |
|||||||||||||||||||
D1 |
|
|
|
|
|
íà |
|
|
|
х шляхах отона зсувачi |
|
|||||||||
А тепер. поставимо |
|
|
îá |
|
|
|
|
|
|
|
|
|
àç |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
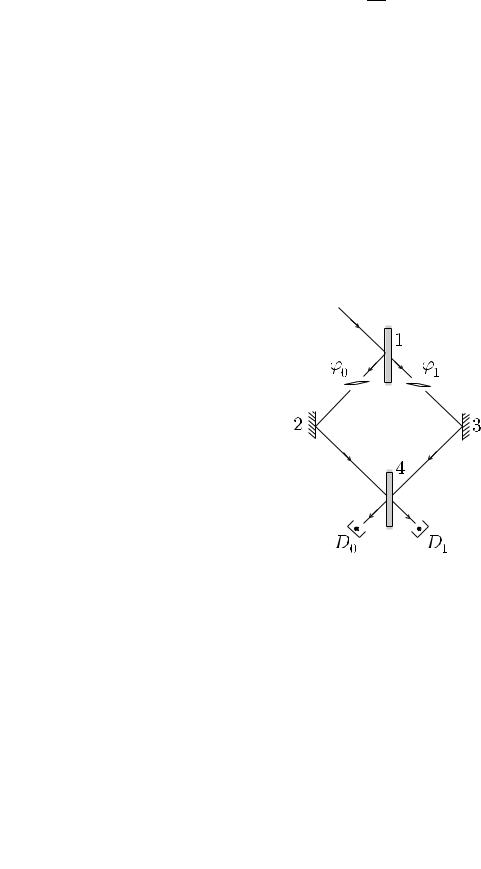
ϕ0 |
ϕîìï'þòå1 (äèâ. èñîì.. 76) i |
|
|
|
|
|
|
|
пристрiй, який i ¹ |
|
|
||||||||||
ис. 76. Одноквабiтовий êвантовий комп'ютер. |
751 |
|
