
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf
Од е зi стандартних означень |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ïîëiíîìà Ëà åððà ç |
||||||||||||||||||||||||||||||||||
усталеíою в теоретичнiй iзицi iíäïри¹днаногоексацi¹ю таким (див. виноску |
|||||||||||||||||||||||||||||||||||||||||||||||||||
íà ñòîð. 344): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
Lp(x), |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
äå ïîëiíîì Ëà åððà Lpk(x) = |
k |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Якщо взяти |
|
|
|
|
|
|
|
|
|
Lp(x) = ex dx |
|
|
e−xxp |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ïîëiíîì |
|
|
|
k = 2l простих,+ 1 à p = n + l, òî ç òî÷íiñòþ |
перетворень,стало¨наш |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2l+1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
безма¹м ментарiвL(x) збiга¹тьсяряд з полiномомдiбнихL |
до попереднiх(x). Справäi, виконуючи |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n+l |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
d |
|
|
|
2l+1 |
|
|
|
|
d |
|
n+l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ln2l++1l (x) = |
|
|
|
|
|
|
|
|
ex |
|
|
|
|
|
|
e−xxn+l |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
dx |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
= |
|
d |
|
2l+1 |
|
|
d |
|
|
− 1 |
n+l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
xn+l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
dx |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
= (−)n+l |
|
|
|
|
|
2l+1 n+l |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|||||||||||||
d |
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
− |
|
d |
|
xn+l |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(n + l)! |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
dx |
|
|
|
|
|
|
k=0 |
(n + l k)!k! |
dx |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
n−l−1 |
|
|
|
|
|
|
|
(n + l)! |
|
|
|
|
|
|
|
|
(n + l)! |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
= (−)n+l |
|
(−)k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn−l−1−k |
|
|||||||||||||||||||||||||
|
(n + l |
− |
k)!k! (n |
− |
l |
− |
1 |
− |
k)! |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
k=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= (−)n+l(n + l)! |
|
|
|
|
1 |
|
|
|
|
xn−l−1 − |
|
(n + l) |
|
|
1 |
|
xn−l−2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
(n − l − 1)! |
|
|
|
1! |
|
|
|
|
(n − l − 2)! |
|||||||||||||||||||||||||||||||||||||||||
+ · · · + (−)n−l−1 |
|
|
|
|
|
|
(n + l)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
(2l + 1)!(n − l − 1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
= (−)n+l(−)n−l−1(n + l)! |
|
|
|
|
|
(n + l)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
(2l + 1)!(n |
|
− |
|
l |
|
− |
1)! |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
23 I. О. Вакарчук( x)n |
|
|
l 1 + (2l + 1)! (n − l − 1) ( |
x)n |
l |
2 + |
|
+ 1353. |
|||||||||||||||||||||||||||||||||||||||||||
× |
(2l + 1)! |
− |
|
|
|
|
− − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
− − · · · |
|
|||||||||||||||
(n + l)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n + l − 1)! |
||||||||||||||||||||||||||||||||||

Вираз у iгурних дужках i ¹ нашим полiномом L(x). Îòæå,
|
|
|
|
2l+1 |
|
|
|
[(n + l)!]2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Використовуючи для |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
−(2l + 1)!(n |
|
|
l |
|
|
|
|
|
1)! L(x). |
|
|
|
||||||||||||||||||||
|
|
|
Ln+l (x) = |
− |
− |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
записати, що |
|
|
L(x) його компактний вигляд, можна також |
|||||||||||||||||||||||||||||
|
|
2l+1 |
|
|
|
(n + l)! |
|
(2l+1) |
|
x |
|
|
|
|
d |
|
|
n−l−1 |
|
|
x n+l |
|||||||||||
|
|
чином, отриму¹мо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
e |
|
dx |
|
|
|
e− x . |
|||||||||||||||||
ТакимLn+l |
(x) = |
−(n − l − 1)! x− |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
(2l + 1)!(n |
|
|
|
l |
|
|
1)! |
|
|
|
2l+1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
радiально¨разомперепозначаючихвильово¨ункцi¨сталiв таве- |
|||||||||||||||||||||||
комуличини,Збираючивиглядi:запишемодержанiw(x) =виразрезультатиa äëÿ |
|
|
− − |
|
|
|
|
|
L |
|
|
|
(x). |
|
||||||||||||||||||
|
|
|
|
|
|
− 0 |
|
|
[(n + l)!]2 |
|
|
|
|
|
|
|
|
|
|
n+l |
|
|
|
|
||||||||
|
|
|
Rn,l(r) = Cn,l |
2ρ |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2ρ |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2l+1 |
|
|
|
||||||||||||||||||
äå |
|
|
|
e−ρ/nLn+l |
|
, |
|
|
||||||||||||||||||||||||
|
|
n |
n |
|
|
|||||||||||||||||||||||||||
Cn,l постiйна нормування. Повна хвильова ункцiя |
||||||||||||||||||||||||||||||||
повинна нормуватисьψ íà (одиницю,r) = Y (θ,тобтоϕ)R |
n,l |
(r) |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
n,l,m |
|
|
|
l,m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
à ó |
|
|
|
координатах |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
с еричних |
|
(r)| dr |
= 1, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
Z |
|ψn,l,m |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
2π |
|
π |
|
|
|
|
|
|
2 |
|
|
∞ |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
||||
Iнтеункцi¨:одиницю,рализакутамиiзвiдси черезвиплива¹нормованiстьумова нормуванняс ерично¨для радiально¨ункцi¨да- |
||||||||||||||||||||||||||||||||
þòü |
Z0 |
dϕ Z0 |
sin θ dθ |
|Yl,m(θ, ϕ)| |
|
Z0 |
|
r |
|
|Rn,l(r)| |
|
dr = 1. |
||||||||||||||||||||
|
|
|
|
|
|
Z0 |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
354 |
|
|
|
|
|
r2Rn,l2 (r)dr = 1. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||

Знайдiмо з цi¹¨ умови величину Cn l:
Óâåäiìî Cn,l |
Z0 |
|
n |
|
2l |
e− |
|
|
|
|
|
Ln+l |
|
n |
|
|
2 |
r dr = 1. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
∞ |
|
2ρ |
|
|
|
|
|
|
|
|
2ρ/n |
|
|
|
|
2l+1 |
|
2ρ |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
çìiííó |
x = 2ρ/n = 2r/naB, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
äå iíòå ðàë |
|
|
|
|
|
|
|
|
|
|
|
|
Cn,l2 |
|
|
|
2 |
|
|
|
I = 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
naB |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
зОбчпрè |
|
|
|
|
|
|
|
|
I = |
Z0 |
∞ |
2l+2 |
e− |
x |
h |
2l+1 |
|
|
|
|
|
i |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
Ln+l |
(x) dx. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
слю¹мо¹днанихйого,полiномiввикористовуючиЛаерра: компактний вираз для одного |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Iíòå= − Z0 |
∞ |
|
|
2l+2 |
2l+1 |
|
|
|
|
|
|
(n + l)! |
|
|
x− |
(2l+1) |
|
d |
|
|
n−l−1 |
|
x |
|
n+l |
|
||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
Ln+l |
(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
e− |
|
x |
|
dx. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
(n − l − 1)! |
|
|
|
|
|
|
|
|
dx |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
ру¹мо частинами: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
− − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(n + l)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
n−l−2 |
|
|
|
|
∞ |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
= |
|
|
|
− |
(n |
|
|
l |
|
|
1)! |
(xLn2l++1l (x) |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
e−xxn+l |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|||||||
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∞ d xLn2l++1l (x) |
|
|
|
|
|
|
d |
|
n−l−2 |
|
|
|
|
x |
|
n+l |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e− |
|
|
x |
|
|
|
dx . |
|
|
|
|
|
|||||||
Ïîçàiðóâàíтеня да¹льний |
÷ëåí äîðiâíþ¹ íóëåâi, òîìó |
|
багатократне iнте- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
ð |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
− − |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
n−l−1 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
n |
|
|
l |
(n + l)! |
|
|
|
|
|
|
|
|
x |
|
|
n+l |
|
|
|
|
|
2l+1 |
|
|
|
|
|
|||||||||||||||||||||||||||||
УнаслiдокI = (−) |
− |
|
(n l 1)! |
Z0 |
|
|
e− |
|
|
x |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
xLn+l (x) |
dx. |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
òîãî, ùî |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
полiнома:нi пiд iнте ралом |
|
|
|
2l+1 |
(x) |
внесок¹полiномлишестепенядвох найстарших(n −l −1), точленiвпохiд- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Ln+l |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
залишать |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
d |
|
n−l−1 |
|
|
|
2l+1 |
|
|
|
|
|
|
|
|
|
|
n+l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
23* |
|
|
|
|
|
|
xLn+l (x) |
|
|
|
= (−) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
355 |
||||||||||||||||
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
(n + l)![(n −l)x −(n + l)(n −l −1)], |
||||||||||||||||||||||||||||||||||||||||||||||
I = |
|
(n − l − 1)! (n − l) Z0 |
∞ e−xxn+l+1dx |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
[(n + l)!]2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
− (n + l)(n − l − 1) Z0∞ e−xxn+ldx |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
[(n + l)!]2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
|
|
|
|
|
|
|
{(n − l)(n + l + 1)! − (n + l)(n − l − 1)(n + l)!} |
||||||||||||||||||||||
|
(n |
− |
l |
− |
1)! |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
[(n + l)!]3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
|
|
|
|
|
|
|
{(n − l)(n + l + 1) − (n + l)(n − l − 1)} |
|
|||||||||||||||||||||
|
(n |
− |
l |
− |
1)! |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тепер= |
|
[(n + l)!]3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
äля стало¨ нормування2n. |
|
знаходимо |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
(n |
− l |
− |
1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
УжеточнiстюнераздозазнаCn,l = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||||||||||
|
|
|
|
|
4 (n |
− |
l |
− |
1)! |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
азовогочалось,мноФактичнощостажник ла нормування обчислю¹ться |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
−s n4aB3 |
[(n + l)!]3 |
|
|
|
|
|
|
||||||||||||
íîþ àçîþ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
içè÷íiα принципово не значе- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
çручно вибратиα, |
ÿê íå |
вплива¹ на |
|
|
|
|
|
|
при¹днанихрезульт. Тут нам |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
стандартногоучим.цю мiстерiюiксу¹тьсункцi¨:озназнакченнядодатнийормулмiнус, знаходимоузстакалiйхполiноâèнорльово¨остуiв |
||||||||||||||||||||||
точнийЛаванункцi¨Закiнчуючи,ерраятягнетьсвираз.основногодляαнарештi,зiрадiально¨= π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
B |
|
|
− |
l |
− |
1)! |
|
|
|
|
|
|
|
|||||||||
нихпроЦимстанiврухRвиразомелектрона(r(проблема) = çàâåðøóÊïîëi¹ìî |
|
|
2ρ |
|
|
e |
ρ/n |
L |
2l+1 |
2ρ |
. |
|||||||||||||||||||
|
|
|
|
|
|
4 |
|
(n |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
n,l |
|
|
−sn4a3 |
|
|
[(n + l)!]3 |
|
n |
|
|
|
− |
|
|
|
n+l |
n |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ðа)озв'язок.Хвильсьêãîоваквантовомеханiчловногопотенункöiÿàëó äëÿíî¨ зв'язазадачi |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
еплекулонi |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
жить вiд трь х квантових ч сел: |
|
|
|
|
|
|
|
|
|
|
|
ψn,l,m(r) ëèøå |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
квантового чис , |
|||||
|
|
|
|
|
|
|
|
квантовиммагнiтномучислачисломполiта.квантовогоЕнерзлядуiя начислате,що воно,як вин - |
||||||||||||||||||||||
lçнача¹иваютьорбiтальрiвнiмагåíåðогоiтнимквантовогоi¨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
||||||||||||
356 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
En залежить |
||||
головнногоквантового числа,n. Òîé àêò, ùî E
òöåâiäальнонiанавжемагнiйшластосовнокв аннямнтуванняимпов.Ачисломте,ротiвгощо навколоенеретичнiпов'язанийдовiльрiвнiо¨iзиродженiñиметрi¹юуnпросторiне залежитьй гамiль.орбiПро
спричиуказу¹неКратнiстькомуя¹додатковуу¹зоператсиметрiюдодзаймемосьткмиового¹iншихамiльтонiвипадковiстюiнтенаступномуiнтераларалiвворуху. Цяднево¨,хуоператорвипадковiстьзадачi,якяк- |
|||||||||||||||
ãî |
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
цiкавим пит |
|
|
|
ó |
|
|
|
|
|
|
ˆ 2, |
ˆ |
|
||
виродженнями |
|
|
|
|
|
|
L |
Lz |
. Öèì |
||||||
|
|
|
|
|
|
|
|
|
парагра i. |
||||||
|
|
n−1 |
l |
|
n−1 |
|
|
|
|
2 |
|
|
|
||
|
|
X X |
|
X |
|
|
|
|
|
|
|
|
|||
Основному становig =âiäïîâiäà¹1 такий= |
(2íàáiðl + 1)квантових= n . |
чисел: |
|||||||||||||
|
|
l=0 m=−l |
|
l=0 |
|
|
|
|
|
|
|
|
|||
а хвильова ункцiяn = 1, |
|
l = 0, |
|
|
|
m = 0, |
|
|
|
||||||
пiсля простих |
пiдстановок цих чисел у загальнi вирази |
|
|
||||||||||||
|
ψ1,0,0(r) = Y0,0(θ, ϕ)R1,0 |
(r), |
|
|
|
||||||||||
Âiäïîâiäíî åíåð iÿ |
основного |
1 |
|
e− |
ρ |
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
ψ1,0,0(r)стану= |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
qπaB3 |
|
|
|
|
|
|
||||
тьсяНаступнакèìèé,4êâàí-êðàòовимино |
E1 |
|
me4 |
|
|
|
|
|
|
||||||
= − 2~2 . |
|
|
|
|
|
|
|||||||||
|
|
вироджений,числами: çáóджений стан характеризу¹- |
|||||||||||||
|
n = 2, |
|
l = 0, |
|
|
m = 0; |
|
|
|
||||||
Åíåð i¨ |
n = 2, |
|
l = 1, |
|
|
m = 0, ±1. |
|
|
|
||||||
|
|
|
E2 = − |
me4 |
|
|
|
|
|
|
|||||
|
|
|
8~2 |
|
|
|
|
|
|
357 |
|||||

àäiàëüíi |
óíêöi¨ Rn,l(r) визнач ють густину ймовiрностi |
|||
2 |
2 |
|
|
|
4приклад,πr R (räëÿ) розподiлуосновногоелектронно¨станугустинахмàймовiрностiри взд вж радiуса r. Íà- |
||||
|
n,l |
|
|
|
|
|
|
4r2 |
|
|
|
r2R12 0 = a3 e−2r/aB |
|
|
ма¹ максим ченняльзначення прикèäíi |
|
|||
|
|
|
B |
|
електронiмовiрнееличинаíàéiìîâiðíiøèõзносновномувiд |
r = aB |
òæå,üñÿ |
||
|
|
ñò |
i, дорiвню¹наякiйвборiвському.атомiЦеознача¹,воднюрадiусущознаходинайбiльш.О |
|
вiда¹значеньджених aB |
0.529 A |
|
|
|
|
|
|
|
- |
|
класичнистанiв аютьуявленнямбiльшедàвiдстаней¹прочислоорбiтиелектронамакрозмiрисимумiв,проблемiатомавiдядраотже,Кеплера.Функцi¨. Це¹бiльше.вiдпозбу |
|||
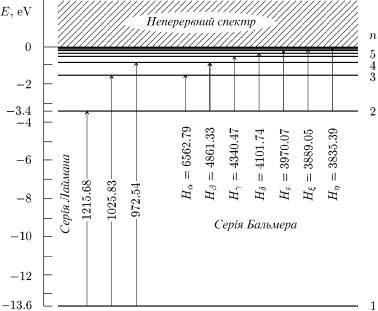
ис. 43. Енер етичнi рiвнi атома водню. Числа бiля лiнiй, що з'¹днують |
|
на¹ атом при переходi електрона мiж цими рiвнями. |
|
рiвнi, довжини хвиль свiтла в ан стремах, яке випромiню¹ або погли- |
|
|
359 |
îñòâiäïîâiäà¹íiõn =òðè,1 lâiäïîâiäíî= 0. |
n = 2 |
-ñòàí âiäïîâiäà¹|2si |prin2pi ipal, |
ментальнаdi use, fundamenсерi¨це.tal,Далiïершiтобтонумелiтерирiзкаацiяанглiйськихст,анiвголовна(для,слiврозмитаsharp,, унда |
||
значаютьСтани з рiзнимиспецiальнимизначеннясиìволами:орбiт льного квантового числа l |
||
|
s |
= 0; |
ïî-станхдять вiдатомамихарактеристики, - анпереходiсерiйз; цих-спектральнихстанстанiв на iншi.лiнiй,Цi.Апозначеннясаме,щовисвiсим |
|||||||||
pчуютьсяволи |
l = 1 |
d |
l = 2 |
f |
|
l = 3 |
|
|
|
s, p, d, |
|
|
|
|
|
|
|
|
|
ським ал авiтом: |
|
|
|
l > 3) йде за латин |
|||||
означа¹, що |
|
g h, . . . . Îòæå, ñò |
ψ1,0,0 позначають як |1si öå |
||||||
÷îìó |
|
|
|
Ïðè äî |
|
ма¹мо стани |
назви |
ïðè |
|
ральнихенерс |
|
|
|
|
m = 0, ±1 |
|
- |
||
|
|
м аких,натомаБальмераякводню,кутовийани,загальакж перехоприйнятi. Надирисдля.43спектзображенiспекталь |
|||||||
|
Ëàðiâíi |
|
|
|
|
|
|
||
|
ëiíié, |
|
|
|
|
|
|
|
|
åòè÷íiðié |
|
|
|
|
|
|
|
|
|
ëiíi¹þ, |
|
|
залежностi |
. Ëiíiÿ |
Hβ |
|
|
||
|
|
частобт |
Hα |
Hβ |
|
|
|
||
|
|
|
|
перех ду |
арактеризуютьс, як ¹ реперною |
||||
аниво дослiдитиз ак |
|
|
розподiл електронно¨. |
густи |
|||||
симетричним.ЦiкСт |
|
|
|
ω = (E4 |
− E2)/~ |
|
|||
|
|
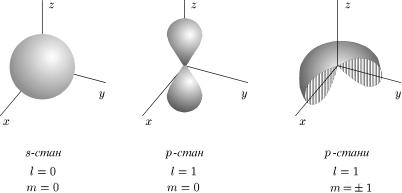
lрозподiлом,= 0 |
полярногоs-кiльки хункцiя |
|
я с ерично |
||||
алежить вiд кутiв (див. ри . 44). Для |
|Y0,0(θ, ϕ)|2 = 1/4π íå |
||||||||
подiл, який залежить вiд |
|
êóòp-ñòàíiâ ìà¹ìî êóòî |
é ðîç- |
||||||
ç |
|
|
|
|
|
θ. Äâà |
æëèâi âèпадки |
||
m = 0 à m = ±1 öi¹¨ |
|
теж зображенi на рис. 44. |
|||||||
íiâèñ. . 44. Кутовий розподiл електронно¨ густини в атомi для рiзних ста-
360

øå äëÿ àò |
|
ùî ò |
|
розподiл за к ами ¹ характерним не ли |
|
|||||||||||||||||||||
а водню,акийдля будь-як го |
|
|
|
|
|
iз центрально-симет |
|
|||||||||||||||||||
р ч им пчимо,тенц алом. Коли атоми вступ ють |
|
|
õiìi÷íèé çâ'ÿçîê, |
|||||||||||||||||||||||
òî |
ер iя молекуляр о¨ |
|
|
|
|
можеатомабув |
|
ìîæ- |
||||||||||||||||||
ë |
веЗазначення при iнших |
|
|
|
озподiл х, хв овi ункцi¨ |
|||||||||||||||||||||
ÿêèõ ¹ лiнiйними комбiнацiями с еðичних ункцiймiнiмальноякi, згiдно |
||||||||||||||||||||||||||
з принципом |
|
|
|
|
|
i¨, êутовихак ж можуть |
iñнувати. Наприклад, |
|||||||||||||||||||
|
|
|
|
|
|
ункцiйсистемиану три новi нормованi хвильовi |
||||||||||||||||||||
утворимоункцi¨: з |
трьсуперпозих |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
Y1,−1(θ, ϕ) − Y1 1 |
(θ, ϕ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
p |
|
= |
= |
|
|
|
3 |
|
sin θ cos ϕ, |
|
|||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
ÿê áàp÷èìî,-îðá òàëiорi¹нтованiавiöiê òèì,вздовжщомаксимумисей густини ймо |
|
||||||||||||||||||||||||
|
| xi |
|
|
|
|
|
√2 |
|
|
|
|
|
|
r |
4π |
|
|
|
|
|||||||
|
|
|
|
|
Y |
1 −1 |
(θ, ϕ) + Y |
1,1 |
(θ, ϕ) |
= r |
3 |
|
|
|||||||||||||
|
|py i = − |
|
|
√ |
2 |
|
|
|
|
|
|
|
4π |
sin θ sin ϕ, |
|
|||||||||||
Цiiрностi,акзва |
i |
|
|
|
|pz = Y1,0(θ, ϕ) = r |
|
|
|
|
|
||||||||||||||||
|
|
|
|
4π cos θ. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
занийдачiнеперервнийногоâ познагiперболiчнихТдлязв'язчеух нях)оротку.ктреяд.Звiдсизнатзупих.ченьпараболiчнихЦезначеньнимосьвиплива¹вiдповiда¹наенерпросторхвильтра¹кторiяхi¨,класичномуîâèõтобтованапррозгункцi. Енерямленiстьвипадку(щода¹мохводнево¨iяй набува¹вiдбитонезв'яруховiхiмiчза |
||||||||||||||||||||||||||
ïî |
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
x, y, z |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
äå |
|
|
|
|
|
|
|
E = |
~2k2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2m |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
спектра,k хвильовийякужевiдзначалосьвектор.адiальнуŸ39,запису¹моункцiю так:для неперервного
|
R(r) = e±ir |
2mE |
причому ункцiя |
~2 rlw, |
|
|
w задовольня¹ те ж iвняння, що й ункцiя |
|
|
ÿäîì,íàêспорiдненимитепеякий вжеобрива¹тьс.неСправдi,полiномом,я.Зауваякщо361- |
|
wжимо,а зобража¹тьсдлядискретногощоункцi¨степеневимспектрааналiтично.рО |
w |
|
