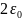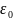- •Часть 1. Расчёт электрического поля в пространстве между электродами цилиндрического конденсатора без объёмного заряда. 7
- •Часть 2. Расчёт электрического поля в пространстве между электродами цилиндрического конденсатора с объёмным зарядом. 14
- •Теоретическое обоснование
- •Часть 1. Расчёт электрического поля в пространстве между электродами цилиндрического конденсатора без объёмного заряда.
- •1.1. Расчёт потенциала и напряжённости поля в конденсаторе.
- •1.2. Определение радиуса границы раздела r12, при котором напряжение делится поровну между слоями.
- •1.3. Определение поверхностной плотности зарядов на поверхности электродов и ёмкости на единицу длины.
- •Часть 2. Расчёт электрического поля в пространстве между электродами цилиндрического конденсатора с объёмным зарядом.
- •2.1. Расчёт потенциала и напряжённости поля в конденсаторе.
- •2.2. Расчёт потенциала и напряжённости в конденсаторе при поменянной полярности электродов.
- •Список используемой литературы
Часть 1. Расчёт электрического поля в пространстве между электродами цилиндрического конденсатора без объёмного заряда.
1.1. Расчёт потенциала и напряжённости поля в конденсаторе.
|
|
|
|
|
|
0,01 |
0,05 |
0,025 |
|
|
10 |
Дано:
Решение:
Область расчёта электрического поля конденсатора представляет собой пространство между его электродами и состоит из двух подобластей: 1 – внутренний слой диэлектрика и 2 – внешний слой. Согласно условию задачи, во внешнем и внутреннем слое диэлектрика объёмный заряд отсутствует, и распределение потенциала находится с помощью уравнения Лапласа. Принимая во внимание условие, что поле конденсатора изменяется вдоль координаты, перпендикулярной поверхности электродов (координаты r) выбираем цилиндрическую систему координат для записи уравнения:
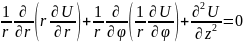
Учитывая симметрию
поля относительно оси конденсатора,
принимаем Eφ=0
и, следовательно,
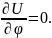 Кроме того, поле цилиндрического
конденсатора является плоскопараллельным
(картина поля во всех плоскостях,
перпендикулярных оси конденсатора,
одинакова), и, следовательно, Ez=0
и
Кроме того, поле цилиндрического
конденсатора является плоскопараллельным
(картина поля во всех плоскостях,
перпендикулярных оси конденсатора,
одинакова), и, следовательно, Ez=0
и
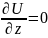 .
Таким образом, уравнение Лапласа
принимает вид:
.
Таким образом, уравнение Лапласа
принимает вид:
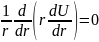
Рассмотрим зависимость потенциала от радиуса цилиндра.
Вследствие наличия между обкладками двухслойного диэлектрика необходимо рассмотреть два случая. Однако, так как нигде нет объёмного заряда, то формулы получатся аналогичными:
При
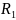 ≤ r
≤
≤ r
≤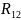 после двукратного интегрирования
уравнения Лапласа по переменной r
получаем следующую зависимость:
после двукратного интегрирования
уравнения Лапласа по переменной r
получаем следующую зависимость:
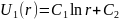 (1)
(1)
При
≤
r
≤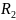 после двукратного интегрирования
уравнения Лапласа по переменной r
получаем аналогичную функцию:
после двукратного интегрирования
уравнения Лапласа по переменной r
получаем аналогичную функцию:
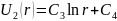 (2)
(2)
Где С1, С2, С3, С4 постоянные интегрирования, которые необходимо найти.
При этом, используя формулу
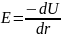
находим распределение напряжённости электрического поля:
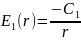 (3)
(3)
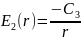 (4)
(4)
Для определения констант C1, C2, C3, C4 воспользуемся граничными условиями:
1. При r= потенциал равен U=0, тогда:
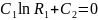 (5)
(5)
2. При r= потенциал равен U= , тогда:
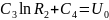 (6)
(6)
3. При r= на границе раздела двух диэлектриков нормальные составляющие вектора электрического смещения равны, тогда: D1n=D2n
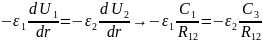
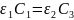 (7)
(7)
4.
При r =
на границе раздела двух диэлектриков
потенциалы
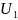 и
и 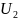 равны, тогда:
равны, тогда:
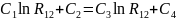 (8)
(8)
Запишем систему уравнений для нахождения постоянных:
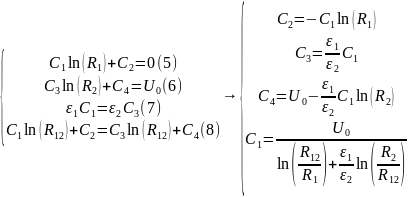
Подставим численные значения:
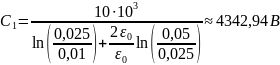
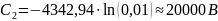
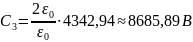
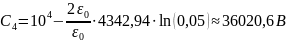
Таким образом, выражения распределения потенциала и напряжённости электростатического поля между электродами цилиндрического конденсатора будет иметь вид:
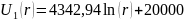
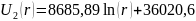
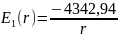
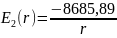
На следующей странице приведены графики распределения потенциала и напряжённости поля в конденсаторе.
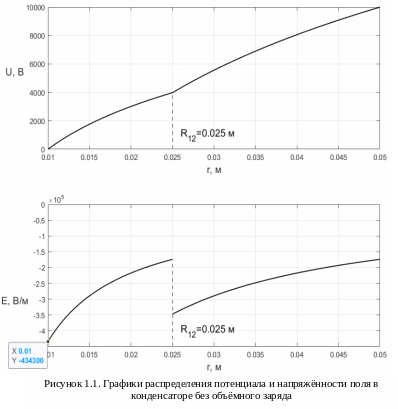 По построенным
зависимостям можно сделать вывод о том,
что потенциал скачков не имеет, а функция
напряжённости терпит разрыв. Потенциал
имеет возрастающий характер. Модуль
напряжённости всегда убывает. Из графика
распределения напряжённости видно, что
максимальное по модулю значение
наблюдается при r = R1
и оно равно |Emax|=434300 В/м.
По построенным
зависимостям можно сделать вывод о том,
что потенциал скачков не имеет, а функция
напряжённости терпит разрыв. Потенциал
имеет возрастающий характер. Модуль
напряжённости всегда убывает. Из графика
распределения напряжённости видно, что
максимальное по модулю значение
наблюдается при r = R1
и оно равно |Emax|=434300 В/м.
1.2. Определение радиуса границы раздела r12, при котором напряжение делится поровну между слоями.
Для определения радиуса границы раздела R12, при котором напряжение делится поровну между слоями, к системе уравнений (5), (6), (7), (8) добавляется ещё одно:
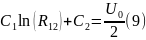
Подставляя выражения
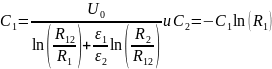 выражаем R12:
выражаем R12:
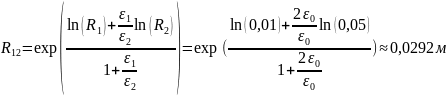
Тогда постоянные интегрирования будут иметь следующие значения:
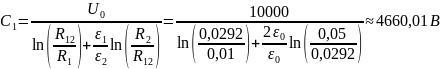
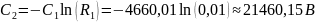
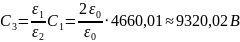
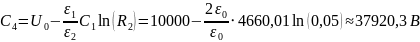
Значит функции распределения потенциала и напряжённости имеют вид:
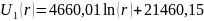
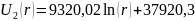
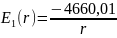
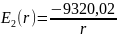
На следующей странице приведены графики распределения потенциала и напряжённости поля в конденсаторе.
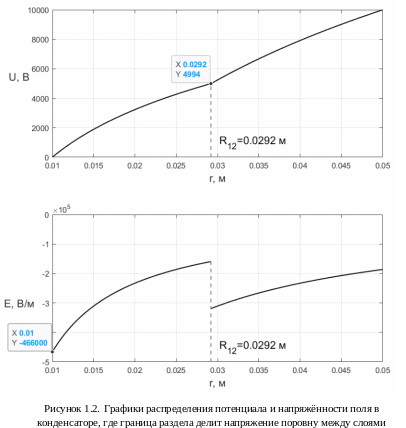 Из
графика распределения потенциала видно,
что при значении R12=0,0292 м
потенциал делится примерно поровну
между слоями. По распределению
напряжённости видно, что максимальное
по модулю значение наблюдается при
r = R1
и оно равно |Emax|=466000 В/м.
Из
графика распределения потенциала видно,
что при значении R12=0,0292 м
потенциал делится примерно поровну
между слоями. По распределению
напряжённости видно, что максимальное
по модулю значение наблюдается при
r = R1
и оно равно |Emax|=466000 В/м.

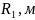
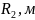
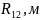
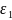
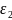
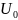 ,
кВ
,
кВ