Полная система уравнений электромагнитного поля в дифференциальной форме.

; ; ; ; ; ; .

Представленная полная система уравнений позволяет рассчитывать любые электромагнитные поля. В частных случаях для расчета могут потребоваться только некоторые уравнения из системы. Для решения системы дифференциальных уравнений необходимо задать граничные и начальные условия, соответствующие рассматриваемой конкретной задаче. Для задания граничных условий необходимо представлять, как изменяются векторы в электромагнитном поле на границах раздела сред с раз личными свойствами.

Граничные условия

Граничные условия в электростатическом поле.

1. На поверхности раздела диэлектриков.

₁ ₂ ₁ ₂

b c

E₂ ( D₂) S_т1 D₂

₂ ₂

₁ ₁ S_т2

a d

S_бок

E₁ (D₁) D₁

а) б)

Рисунок 1-1

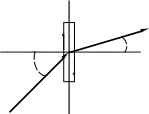
На границе раздела двух диэлектриков с различными диэлектрическими проницаемостями ₁ и ₂ (рис. 1-1) происходит преломление векторов напряженности и смещения. Границу в малой окрестности рассматриваемой точки считаем плоской. Применяя к малому прямоугольному замкнутому контуру «abcda» (рис.1-1 а), длинные стороны которого параллельны границе и вплотную прилегают к поверхности раздела, запишем закон электромагнитной индукции, учитывая, что магнитный поток сквозь бесконечно малую площадку, ограниченную контуром «abcda», равен нулю:

.

Представив этот интеграл в виде суммы, получим:

.

Н а отрезках ab и cd, ввиду их малости, считаем напряженность одинаковой и равной соответственно и Интегралами по отрезкам bc и ad контура пренебрегли, так как они бесконечно малы по сравнению с отрезками ab и cd (bc= ad<< ab= cd). Окончательно можем записать:

или .

На поверхности раздела сред с различными диэлектрическими проницаемостями равны касательные (по отношению к границе) составляющие векторов напряженности электрического поля.

Для замкнутой поверхности, образованной боковой поверхностью цилиндра и двумя торцевыми поверхностями, расположенными вплотную к поверхности раздела диэлектриков, (рис.1-1 б), применяя постулат Максвелла, можем записать:

.

Интегралом по боковой поверхности цилиндра пренебрегаем ввиду его малости, по сравнению с интегралами по торцам, в пределах которых считаем векторы электрического смещения постоянными и равными соответственно и . Потоки через торцы разного знака, так как один из них входит в поверхность, а другой выходит, поэтому, сократив на можем записать:

; .

На поверхности раздела диэлектриков отсутствует поверхностные заряды ( = 0). Запишем окончательно граничные условия для вектора электрического смещения:

или

На поверхности раздела сред с различными диэлектрическими проницаемостями равны нормальные (по отношению к границе) составляющие векторов электрического смещения.

Поделив соотношения, записанные для составляющих векторов, получим условия преломления векторов на границе раздела: