Теорема Гаусса и постулат Максвелла в дифференциальной форме.
Применим указанные законы для весьма малой поверхности S0 , ограничивающей объем V с зарядом q:
;
.
Для получения соотношений, связывающих заряды с векторами напряженности и смещения в некоторой точке внутри поверхности, необходимо перейти к пределу, устремив поверхность S0 и объем V к нулю, оставаясь в окрестности этой точки.
Рассмотрим предел отношения обеих частей уравнений к объему V, при V стремящемся к нулю:
;
.
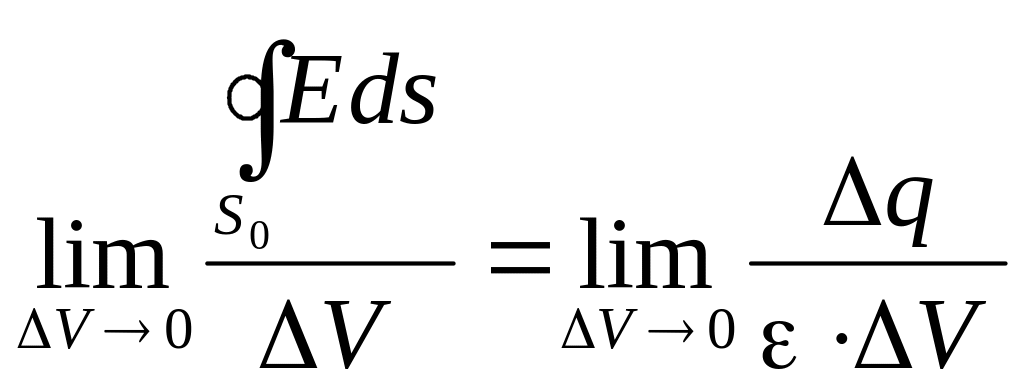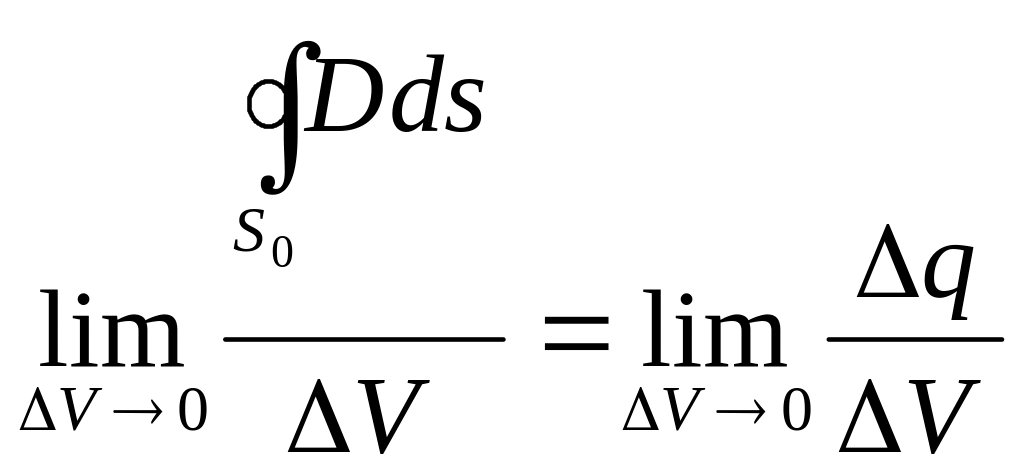Предел отношения потока некоторого вектора сквозь поверхность S0 к объему V, ограниченному этой поверхностью при V, стремящемся к нулю, называется расхождением или дивергенцией данного вектора в точке, в которую стягивается объем V. Предел отношения заряда, находящегося в данном объеме, к величине V, когда этот объем стремится к нулю, равен объемной плотности заряда в той же точке. Учитывая сказанное, запишем теорему Гаусса и постулат Максвелла в дифференциальной форме:
; 
.
Термин «расхождение»
легко понять, если вспомнить, что силовые
линии векторов напряженности и смещения
начинаются и заканчиваются на зарядах.
В тех точках поля, где
= 0,
и
– расхождение линий из этих точек
отсутствует. Линии из этих точек не
расходятся и не сходятся к ним, а могут
лишь проходить через эти точки.
Указанные соотношения в дифференциальной форме связывают характеристики электрического поля в любой точке. Они записаны в инвариантной форме и могут быть использованы в любой системе координат.
Рассмотрим
запись дивергенции вектора в декартовой
системе координат. Для этого воспользуемся
векторным дифференциальным оператором
«набла» (
),
который записывается в виде суммы трех
ортогональных составляющих:
Так как дивергенция вектора является скалярной величиной, то ее можно представить в виде скалярного произведения оператора «набла» на соответствующий вектор, в результате такого умножения получаем сумму производных коллинеарных составляющих векторов:
.
Запись дивергенции в других системах координат приводится в математических справочниках.
Запишем по аналогии принцип непрерывности магнитного потока в дифференциальной форме:
Расхождение линий индукции в любой точке магнитного поля равно нулю, т.е. эти линии являются замкнутыми кривыми. Если будет открыт предсказанный теоретически Дираком магнитный заряд (монополь Дирака), то последнее уравнение изменится и в тех точках, где будет существовать магнитный заряд, в правой части уравнения вместо нуля появится плотность магнитного заряда, и это уравнение уже не будет называться принципом непрерывности.
Закон полного тока и закон электромагнитной индукции в дифференциальной форме.
Применим названные законы для малого контура l0, ограничивающего некоторую поверхность S, сквозь которую проходит ток i (либо магнитный поток Ф). Стягивая контур l0, в точку, т.е. устремляя S к нулю, рассмотрим пределы отношений обеих частей уравнений к величине S, при ее стремлении к нулю:
;
(В законе электромагнитной индукции в правой части стоит частная производная по времени, так как поток изменяется и во времени и за счет уменьшения размеров площадки S, охваченной контуром интегрирования).
Для правой части закона полного тока можем записать:
,
где – угол между вектором плотности тока и нормалью к поверхности, ограниченной контуром интегрирования lo. Предел отношения в левой части уравнения называется проекцией ротора вектора на ту же нормаль:
.
Ориентируя нормаль к площадке вдоль осей координат, получим равенство всех компонентов рассматриваемых векторов. Это означает, что оба вектора равны друг другу. Поэтому можем записать закон полного тока в векторной форме:
.
Ротор вектора также является вектором, поэтому записанное уравнение содержит три уравнения для проекций вектора и является инвариантным по отношению к системе координат. Записать это уравнение в декартовой системе координат можно с помощью оператора «набла», применяя операцию векторного умножения:
=
= (
)
+
(
)
+
(
)
.
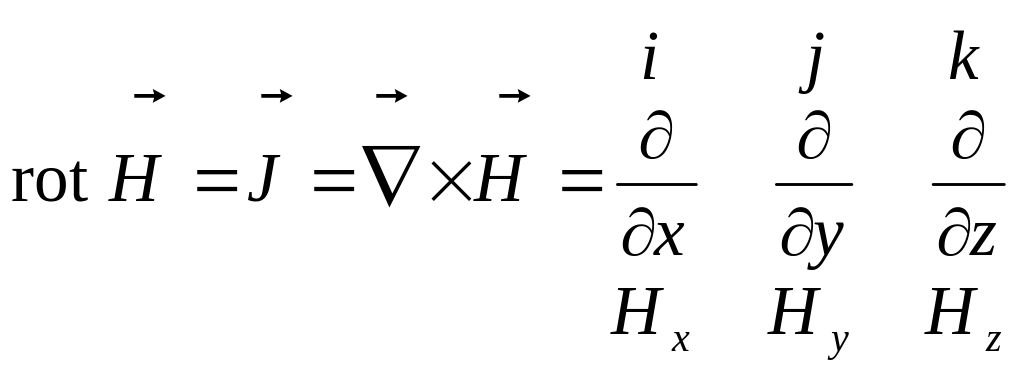В скобках записаны проекции вектора плотности тока на оси координат:
Jx=
;
Jy=
;
Jz=
.
По аналогии запишем выражение для закона электромагнитной индукции:
.
Оно также содержит три уравнения для проекций.