
1
Лекция 5
Расчет электрической емкости.
Из первой части курса ТОЭ нам уже известно, что электрическая емкость (С ) зависит от геометрических параметров (размеров и формы тела) и от диэлектрической проницаемости среды, в которой оно находится: С = f(g, )
Для уединенного тела емкость является коэффициентом пропорциональности между зарядом тела и его потенциалом (при выборе точки нулевого потенциала в
бесконечности): C = Uq . Для двух проводящих тел с одинаковыми по величине
зарядами разного знака емкость между этими телами является коэффициентом пропорциональности между зарядом одного их тел и разностью потенциалов
|
q1 |
|
q |
|
(напряжением) между ними: C = |
|
= |
|
. |
U 1 −U 2 |
u |
|||
Потенциальные коэффициенты, коэффициенты электростатической индукции и частичные емкости в системе заряженных тел.
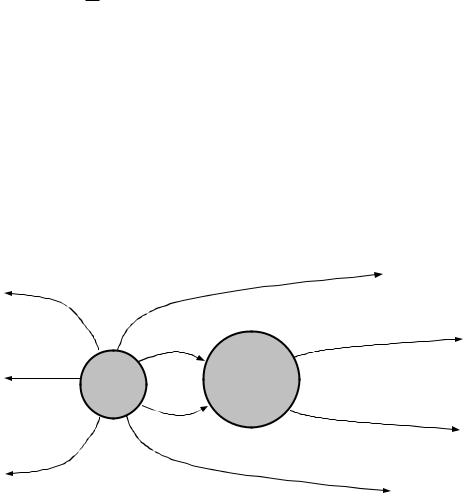
Рассмотрим систему из двух проводящих тел (рис.5–1). Пусть заряжено только одно из тел, а заряд второго равен нулю (q1 = q, q2 = 0). Приближение второго тела к первому изменяет поле созданное зарядом на первом теле из-за перераспределения заряда на первом теле и из-за появления наведенных зарядов на поверхности второго тела.
|
– |
+ |
|
– |
+ |
+q1 |
– |
q2 = 0 + |
Рисунок 5–1
Потенциалы обоих тел пропорциональны заряду первого тела и зависят от размеров тел, их взаимного расположения и диэлектрической проницаемости:
U1 = 11·q1 ; U2 = 21·q1
Коэффициент 11, называемый собственным потенциальным коэффициентом первого тела, зависит от наличия второго тела. Коэффициент 21
называется взаимным потенциальным коэффициентом между первым и вторым телом.
Если заряжены оба тела, то потенциал каждого из них зависит от обоих зарядов и может быть в линейной системе на основе принципа наложения представлен в виде:
U1 = 11·q1 + 12·q2; U2 = 21·q1 + 22q2.
Собственные потенциальные коэффициенты имеют два одинаковых индекса, а взаимные – два различных. Измеряются они в 1/Ф.

2
Если заряды двух тел равны и противоположны по знаку (q1 = – q2 = q), то выражение для емкости в системе двух тел получаем в виде:
C = |
q1 |
= |
q |
= |
1 |
. |
U 1 −U 2 |
q ( 11 − 12 − 21 + 22 ) |
11 + 22 − 2 12 |
Для системы из « n » заряженных тел в линейной среде на основе принципа наложения можем записать:
U1 = 11·q1 + 12·q2 + . . . + 1n·qn;
U2 = 21·q1 + 22·q2 + . . . + 2n·qn;
(5 –1)
Un = n1·q1 + n2·q2 + . . . + nn ·qn.
Собственные потенциальные коэффициенты можно определить экспериментально. Для этого надо только одно из тел (например, второе) подключить к источнику т.е. зарядить его до потенциала U2 = 22·q2 = U0 Заряды остальных тел должны быть равны нулю. После отключения источника второе тело разряжается через баллистический гальванометр и при этом измеряется его заряд и рассчитывается
собственный потенциальный коэффициент:
|
22 |
|
=U q
2 2
. Однако потенциальные
коэффициенты чаще всего определяют расчетным путем.
Если уравнения (5–1) записать иначе, выразив заряды тел через их потенциалы, то система уравнений примет вид:
q1 = 11·U1 + 12·U2 + . . . + 1n·Un; q2 = 21·U1 + 22·U2 + . . . + 2n·Un;
(5 –2)
qn = n1·U1 + n2·U2 + . . . + nn Un.
Коэффициенты , измеряемые в фарадах, называются коэффициентами электростатической индукции, собственные с одинаковыми индексами и взаимные с различными индексами. Коэффициенты электростатической индукции образуют матрицу, получаемую обращением матрицы потенциальных коэффициентов .
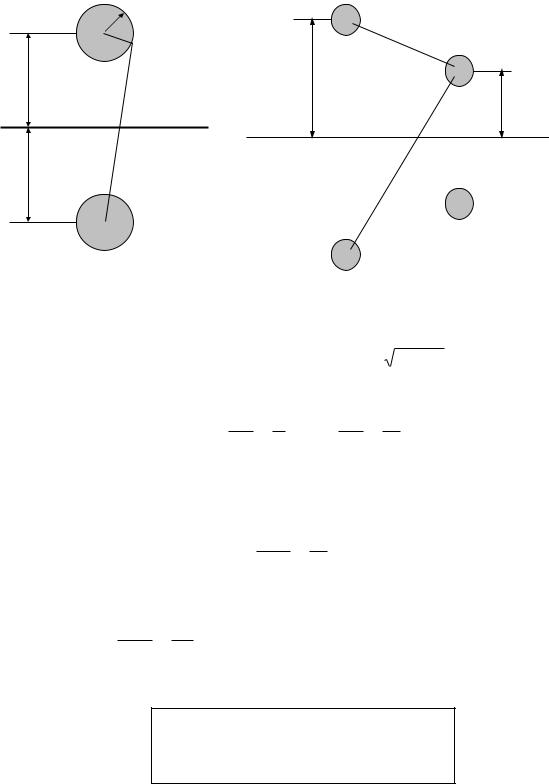
Коэффициенты электростатической индукции очень просто определяются экспериментально. В системы из трех проводящих тел (рис. 5–2) определим коэффициенты 11 и 13. Заземлим все тела кроме первого, это означает, что U2 = U3 = 0. Первое тело зарядим от источника постоянного напряжения до потенциала U1 = U0 , считаем его заряд равным q1 >0. На втором и третьем телах вследствие электростатической индукции появятся заряды противоположного знака q2<0, q3<0.
q1 |
q3 |
|
q2 |
G1 U0 |
G3 |
Рисунок 5–2
При этом заряды всех тех тел определяются потенциалом U1 = U0: q1 = 11·U1; q2 = 21·U1; q3 = 31 U1 . Если первое тело разрядить через гальванометр G1, который измерит величину заряда q1, то освободятся также и наведенные заряды q2 и q3,

3
причем последний будет измерен гальванометром G3. Зная величины этих зарядов легко рассчитать коэффициенты электростатической индукции:
|
|
= |
q1 |
0 ; |
|
|
= |
q3 |
0 . |
11 |
|
31 |
|
||||||
|
U1 |
|
|
U1 |
|
||||
|
|
|
|
|
|
||||
Во всех случаях собственные коэффициенты электростатической индукции больше нуля, а взаимные – меньше нуля: kk > 0, kp < 0.
Существует еще одна форма записи уравнений в системе заряженных тел, при которой заряды выражаются через разности потенциалов:
q1 = C11·(U1-0) + C12·(U1 - U2)+ . . . + C1n·(U1 -Un);
q2 = C21·(U2 -U1)+ C22·(U2-0)+ . . . + C2n·(U2-Un);
(5 –3)
qn = Cn1·(Un -U1) + Cn2·(Un -U2)+ . . . + Cnn ·(Un -0).
Коэффициенты этого уравнения (Ckk и Ckp) называются собственными и взаимными частичными емкостями и измеряются в фарадах.
Определим связь между коэффициентами электростатической индукции и частичными емкостями, сопоставляя системы уравнений 5 –2 и 5 –3.
1. Приравняв потенциалы всех тел к потенциалу первого тела (Uk = U1) из
первых уравнений обеих систем получим: q1 = C11U1 = ( 11+ 12+ 13+ …+ 1n)U1 , откуда:
C11 = 11+ 12+ 13+ …+ 1n.;
n C kk = kp p=1
.
2. Приравняв потенциалы всех тел, кроме первого, к нулю (Uk = 0; U1 ≠ 0) из
первых уравнений обеих систем получим: q1 = 11U1 = (C11+C12+C13+ …+C1n)U1, откуда:
|
|
n |
|
|
|
|
11 = C11+C12+C13+ …+C1n; |
kk = С kp . |
|
|
|
|
|
p=1 |
|
|
|
|
|
|
|
|
|
3. Приравняв потенциал первого тела к нулю (U1 = 0), получим |
: |
|
|
||
|
|
||||
q1 = 12U2 + 13U3 + … + 1nUn = – C12U2 – C13U3 – …– C1nUn , откуда: |
|
Ckp = – kp |
|||
|
|
|
|
|
|
Уравнениями, записанными через частичные емкости (5–3), пользоваться удобнее, так как все частичные емкости являются положительными. Очевидно, что, зная любую матрицу коэффициентов, легко определить все остальные.
Для расчета напряжений между телами в системе проводников обычно пользуются частичными емкостями, с помощью которых легко построить расчетную схему емкостной цепи. Рассмотрим в качестве примера систему из трех проводящих тел над землей (рис. 5–3а), два из которых не заряжены, а потенциал первого тела по отношению к земле равен U0 из-за подключенного источника постоянного напряжения. Изобразив на рисунке частичные емкости тел в рассматриваемой системе, можем нарисовать эквивалентную схему цепи (рис.5–3б) для расчета напряжений на участках.
|
1 |
|
|
|
|
|
C13 |
3 |
|
|
|
|
|
C13 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
C12 C23 |
|
|
|
|
|
C12 |
|
|
|
C23 |
|||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
U0 |
|
|
|
C11 |
|
|
|
|
|
C33 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
C22 |
|
|
|
|
|
|
|
U0 C11 |
|
C22 |
|
|
C33 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
U = 0 |
|
а) |
б) |
|
Рисунок 5–3 |
Потенциальные коэффициенты в системе тонких, параллельных весьма длинных проводов.
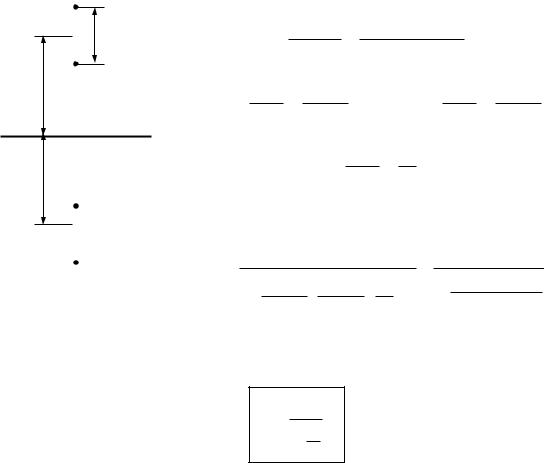
1.Один провод над землей. Рассматривая поле как плоскопараллельное, воспользуемся методом зеркальных изображений (рис.5–4а).
|
R |
|
1 |
|
r1 |
|
r12 |
|
|
|
2 |
h |
r2 |
h1 |
h2 |
h
r1/2 |
|
|
|
|
|
|
|
|
|
|
2/ |
1/ |
|
|
|
|
|
а) |
|
|
|
|
б) |
Рисунок 5–4 |
|
|
|
|
|
Для тонкого цилиндра, считая, что h >> R , т.е. b = |
h |
2 |
− R |
2 |
h |
|
|
эквивалентный заряд на проводе равный , расположен на его геометрической оси, запишем выражение для потенциала:
|
|
|
r |
|
/ |
|
|
2h |
U = |
|
ln |
2 |
+ C |
= |
|
ln . |
|
|
|
|
|
|||||
|
2 |
|
r |
|
|
|
2 |
R |
|
|
|
1 |
|
|
|
|
|
Полагая, что постоянная С / = 0, получаем, что точки поверхности нулевого потенциала равноудалены от зарядов (r1 = r2), т.е. потенциал равен нулю на поверхности земли. Представив заряд отрезка провода длиной « l » в виде q = l, определим собственный коэффициент электростатической индукции:
11 = 2 1 l ln 2Rh .
2. Два провода над землей.
Для случая двух проводов над землей (рис.5–4б) по аналогии можем записать:
|
|
= |
1 |
ln |
2h |
|
|
|
|
1 |
|||
|
|
|
|
|
|
|
|
11 |
|
2 l |
|
R |
|
|
|
|
|
1 |
||
|
|
|
|
|
|
|
;
|
|
|
1 |
|
2h |
|
|
|
|
|
1 |
|
r1/ 2 |
|
|
|
|
= |
|
ln |
2 |
; |
|
|
= |
|
= |
|
ln |
|
. |
22 |
|
|
12 |
21 |
|
|
|||||||||
|
|
2 l |
|
R 2 |
|
|
|
2 l |
|
r12 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
В общем случае произвольного количества проводов собственные и взаимные коэффициенты электростатической индукции вычисляются из соотношений:
5
|
|
= |
1 |
ln |
2hk |
; |
|
= |
1 |
ln |
rk / p |
. |
|
kk |
2 l |
R k |
kp |
2 l |
rkp |
||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
Емкость двухпроводной линии с учетом влияния земли.
Рассмотрим двухпроводную линию, провода которой расположены друг над другом на расстоянии D со средней высотой подвеса над землей, равной h (рис. 5-5). Мы уже получили формулу для расчета емкости через потенциальные коэффициенты, подставляя в которую собственные и взаимные потенциальные коэффициенты рассматриваемых тонких проводов (R << h, R << D), определим емкость исследуемой двухпроводной линии:
1
D
2
h
h
2/
1/
Рисунок 5–5
11
C =
|
C = |
|
|
q |
|
|
= |
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
U |
1 |
−U |
2 |
|
|
|
+ |
|
|
|
|
|
|
|
|
11 |
|
||
= |
1 |
ln |
2h + D |
; |
|
|
||||
2 l |
|
|
R |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
= |
|
|
1 |
ln |
|
|
|
|
12 |
2 l |
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
2 l |
|
|
|
2h − D |
|
2h + D D |
|
ln |
|
|
|
|
|
R |
|
R |
2h |
|
|
|
|
|
|
1 |
|
|
22 |
− 2 |
|
12 |
|
|
= |
1 |
ln |
2h − D |
|
22 |
2 l |
R |
||||
|
|
|
||||
|
|
|
|
|||
2h |
|
|
|
|
||
D |
|
|
|
|
|
|
|
|
|
= |
|
|
2 l |
|
|
|
|||
|
2 |
|
|
(4h |
2 |
− D |
2 |
)D |
2 |
|||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
4h |
2 |
R |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
;
Емкость двухпроводной линии без учета влияния земли (h >> D) можно записать в виде:
= l
C
ln DR
Емкость трехфазной линии передач.
Длина бегущих волн в линиях с частотой 50 Гц составляет 6000 километров, поэтому для реальных линий длиной до нескольких сотен километров можно считать, что токи и напряжения в линиях имеют практически постоянную начальную фазу, не зависящую от координаты. При таком допущении поле в каждый момент времени можно считать статическим и использовать выводы, полученные выше. Следует лишь иметь в виду, что заряды, токи и потенциалы проводов представлены в комплексном виде, так как необходимо учитывать сдвиг фаз между ними. Запишем уравнения для зарядов трех проводов в комплексном виде:

6
q1 = 11U1 + 12U 2 + 13U 3 q2 = 21U1 + 22U 2 + 23U 3 q3 = 31U1 + 32U 2 + 33U 3
Пусть напряжения образуют симметричную систему прямого порядка
j 2
следования фаз. Используя операторный оператор поворота a = e 3 , запишем:
|
j |
4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 = e |
|
3 = |
; |
a3 = 1; |
a + a2 +1 = |
0 ; U 2 = a2U |
1 = |
U1 |
; U 3 |
= aU1 тогда: |
|||||||||||||
|
a |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
||
|
|
|
|
|
|
|
q |
|
= ( |
11 |
+ a2 |
12 |
+ a |
13 |
)U |
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
||||||||
|
|
|
|
|
|
|
q |
2 |
= ( |
22 |
+ a2 |
23 |
|
+ a |
21 |
)U |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
q |
3 |
= ( |
33 |
+ a2 |
31 |
|
+ a |
32 |
)U |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||
При полной симметрии расположения проводов трехфазной линии получаем равенство всех собственных и всех взаимных коэффициентов электростатической индукции:
11= 22= 33= kk ; |
12= 23= 13= kp . |
В этом случае, учитывая, что kp ( a + a2 ) = – kp , предыдущую систему уравнений для зарядов можно представить в виде:
q |
|
=( |
|
|
− |
|
|
|
|
|
|
kk |
kp |
)U |
1 |
||||||
1 |
|
|
|
|||||||
q |
|
=( |
|
− |
|
|
|
|||
2 |
kk |
kp |
)U |
2 |
||||||
|
|
|
|
|
|
|
||||
q |
|
=( |
|
− |
|
|
|
|||
3 |
kk |
kp |
)U |
3 |
||||||
|
|
|
|
|
|
|
||||
.
Выражение, стоящее в скобках является емкостью линии на одну фазу.
Выражая ток в фазе через заряд:
|
|
I |
k |
|
i = |
dq |
|
dt |
||
|
= j q |
k |
|
;
|
= j q |
|
I |
||
= |
j ( |
kk |
|
|
|
, для каждой фазы можно записать:
− kp ) U k .
Так как разность, стоящая в скобках, является при симметричном расположении проводов вещественным числом, то в каждой фазе напряжение и ток сдвинуты по отношению друг к другу на угол = 900, что и следовало ожидать из-за емкостного характера цепи.
Если же расположение проводов несимметрично, взаимные коэффициенты электростатической индукции не одинаковы, и выражения, стоящие в скобках, оказываются комплексными числами, например для первой фазы имеем:
|
= j ( |
|
2 |
|
|
+ a |
|
|
|
|
|
|
|
|
|
I |
1 |
11 |
+ a |
12 |
) U |
1 |
= j (m jn) U |
1 |
= j mU |
1 |
nU |
1 |
|||
|
|
|
|
13 |
|
|
|
|
|||||||
Второе слагаемое имеет одинаковую или противоположную фазу по отношению к начальной фазе тока, что эквивалентно поглощению или выделению активной мощности в этой фазе. Таким образом, несимметричное расположение проводов трехфазной системы приводит к переносу активной мощности между фазами и к неравномерной нагрузке фаз, что нежелательно.
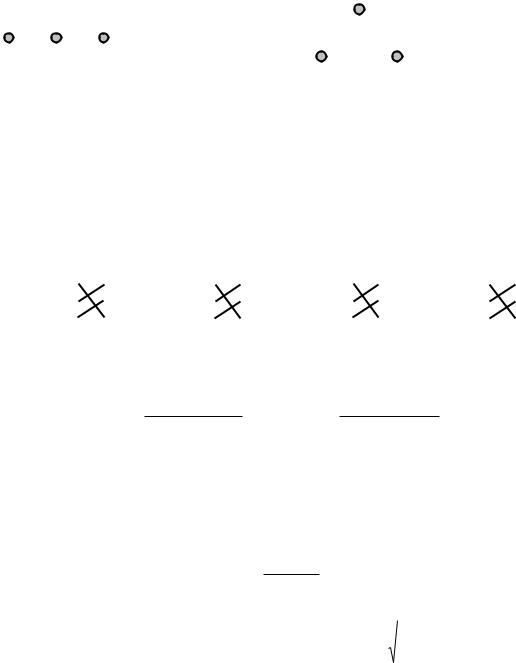
Полную геометрическую симметрию для исключения переноса мощности можно получить только при использовании трехфазного кабеля (рис.5–6). В случае применения воздушных линий передач невозможно достичь симметрии расположения проводов (рис. 5–7а, 5–7б).
1 |
11 = 22 = 33 |
2
12 = 23 = 13
7
|
|
3 |
|
|
|
|
|
|
Рисунок 5–6 |
|
|
||
|
|
|
|
|
1 |
|
1 |
2 |
3 |
|
|
|
|
|
|
2 |
3 |
|
||
|
|
11 = 22 = 33 |
11 ≠ 22 = 33 |
|||
|
|
12 = 23 ≠ 13 |
12 = 13 ≠ 23 |
|||
|
|
|
|
|
|
|
|
а) |
|
|
|
б) |
|
Рисунок 5–7
В воздушных линиях для достижения симметрии применяется транспонирование проводов – периодическое изменение их взаимного положения на опорах через равные интервалы (рис. 5–8).
1 |
|
2 |
|
3 |
|
1 |
2 |
|
3 |
|
1 |
|
2 |
3 |
|
1 |
|
2 |
|
3 |
Для транспонированных линий коэффициентов:
|
|
= |
|
+ |
|
+ |
|
11 |
|
22 |
|
||
|
|
|
|
|
||
|
0 |
|
|
3 |
|
|
|
|
|
|
|
||
Рисунок 5–8 вычисляют средние значения потенциальных
|
33 |
; |
m |
= |
|
12 |
+ |
23 |
+ |
13 |
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
3 |
|
|
|
|
Потенциалы каждой фазы выражаются через заряды, фазы можем записать:
|
|
= q |
+ |
|
q |
|
+ |
|
q |
|
= |
|
+ (a |
2 |
+ a) |
|
|
U |
1 |
m |
2 |
m |
3 |
0 |
|
m |
|||||||||
|
0 1 |
|
|
|
|
|
|
|
|
|
например, для первой
q |
= ( |
0 |
− |
m |
)q |
1 |
|
|
1 |
Отсюда полная емкость каждого провода относительно земли с учетом других проводов равна:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С = |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
m |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Причем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln 23 |
|
h1h2 h3 |
|
|
|
||
|
|
|
1 |
|
|
1 |
|
|
2h |
|
|
|
2h |
|
|
|
2h |
|
|
|
R1R2 R3 |
|
|
|
||||||||||
|
|
= |
|
|
|
|
|
ln |
1 |
|
+ ln |
|
|
2 |
|
+ ln |
3 |
|
= |
|
|
|
|
|
|
; |
||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 l 3 |
|
R1 |
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
2 l |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
R3 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
r12 | |
|
|
|
|
r13 | |
|
|
|
|
r32 | |
|
|
|
|
|||||
|
|
|
|
m |
= |
|
|
|
|
|
|
|
ln |
|
|
|
+ ln |
|
|
+ ln |
|
|
. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
2 l |
3 |
|
|
r |
|
|
|
|
r |
|
|
|
|
r |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
13 |
|
|
32 |
|
|
|
|
|
||||||

8
Метод средних потенциалов (метод Хоу).
Метод основан на предположении о равномерном распределении зарядов на поверхности, либо вдоль осей протяженных проводящих тел. Вычислив при этом предположении потенциал в различных точках проводящих тел, затем находят среднее значение потенциала этих тел, и используют его для расчета потенциальных коэффициентов или емкостей в системе тел:
C = |
q |
или = |
U ср |
. |
|
U ср |
q |
||||
|
|
|
На самом деле в статическом поле потенциалы всех точек проводника одинаковы, а распределение зарядов на поверхности проводника не является равномерным. Однако во многих конкретных случаях неравномерность распределения зарядов оказывается не очень существенной, и результаты расчетов по методу средних потенциалов весьма хорошо согласуются с результатами измерений. Точность метода высока, когда участки тел с неравномерным распределением зарядов не вносят существенного вклада в величину суммарной емкости.
Метод нашел широкое применение при расчете емкостей антенн, сопротивлений заземлителей и других устройств, в которых можно пренебречь неравномерностью распределения источников поля.
Рассмотрим систему двух тонких протяженных проводов, произвольной формы
(рис.5–9а).
|
1 |
|
|
|
|
|
|
dl1 |
|
dl1=dl |
|||
1 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
r |
|
|
|
|
|
|
dl2=dl/ |
|
|
R |
|
|
|
|
dl2 |
2 ≠ 0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
а) |
|
б) |
|||
|
Рисунок 5–9 |
|
|
|
|
|
|
Определим коэффициент 12. |
|
|
|
|
|
Заряд первого провода примем равным нулю, тогда его потенциал можно |
||||||
вычислить из соотношения U1 = 12 q2. Предполагаем, что заряд |
распределен по |
|||||
второму проводу равномерно по длине с линейной плотностью 2 |
= |
q2 |
. |
|||
|
||||||
|
|
|
l2 |
|||
Определим потенциал элемента (dl1) первого провода из уравнения:
U |
* |
= |
1 |
2 dl2 |
|
|
2 l2 |
|
|
|
dl2 |
= |
q2 |
|
|
|
dl2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
4 |
r |
4 l |
|
|
r |
4 l |
|
|
r |
||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 |
|
2 |
||||||||||||||
|
|
|
|
l |
2 |
|
|
|
|
|
l |
2 |
|
|
|
l |
2 |
|
||
Среднее значение потенциала первого провода определим интегрированием вдоль этого провода:
U |
|
= |
1 |
|
U |
* dl = |
q2 |
|
|
dl1dl2 |
, откуда: |
|
|
= |
U 1 |
= |
1 |
|
|
dl1dl2 |
|||||
1 |
|
|
|
|
12 |
|
|
|
|
|
|||||||||||||||
|
|
l |
1 |
1 |
4 l l |
|
r |
|
|
q |
|
|
4 l l |
|
r |
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||
|
|
|
1 l |
|
|
1 |
2 l |
l |
2 |
|
|
|
|
|
|
|
1 |
2 l l |
2 |
|
|
||||
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9
Определение коэффициента 11 (рис 5–9б) производится при двукратном интегрировании вдоль одного и того же проводника. Для того, чтобы расстояние ( r ) не обращалось в нуль, определяют потенциал на поверхности провода, считая что заряд распределен вдоль его оси. При этом rmin = R и выражение для собственного коэффициентов электростатической индукции можно записать в виде:
11 |
= |
1 |
/ |
|
dl / dl |
4 l / l |
r |
||||
|
|
|
l |
l |
|
Определение емкости по картине поля.
Емкость системы из двух проводящих протяженных тел, для которых построена картина плоскопараллельного поля, можно определить по этой картине исходя из нижеследующих соображений. Заряд на конце одной трубки напряженности, опирающейся на поверхность проводника, можно определить, предполагая, что его поверхностная плотность в пределах трубки постоянна:
q = · s = D· s = D·l· a = ·E·l a
Тогда суммарный заряд на проводнике равен сумме зарядов на концах всех построенных трубок напряженности, которые одинаковы ввиду равенства потоков всех трубок ( V = const) q = q·m, здесь m – количество трубок напряженности
электрического поля. Величину напряженности представим в виде:
E = |
U |
|
n |
||
|
.
Напряжение между заряженными телами легко выразить, через приращение потенциала между равнопотенциальными линиями и количество интервалов между ними ( n ) на картине поля: u = U·n.
Подставляя полученные выражения для заряда и напряжения между телами в формулу для емкости, получим:
C = |
q |
= |
m l a E |
= l |
m a U |
= l |
m a |
||
u |
n U |
n U |
n |
n n |
|||||
|
|
|
|
||||||
Принимая во внимание, что в правильно построенной картине поля выполняется условие:
VU
=a = kn
= const
,
окончательно имеем:
C = l |
m |
k |
|
n |
|||
|
|
