1.2. Проекция вектора

Проекцией вектора на заданную осьl называется численное значение векторана осиl(рис. 1.5а).

Проекцией вектора на векторназывается проекция векторана ось, имеющую с векторомодинаковое направление (рис. 1.5б).

Рис. 1.5а Рис. 1.5б

, где- угол между вектороми осьюl.

Свойство проекций:

1) Проекция суммы векторов на ось равна сумме проекций этих векторов, т.е.

Пр_.Пр.+ Пр.;

2) проекция произведения вектора на числоравна произведению числа на проекцию вектора, т.е. Пр_lПр_l.

1.3. Декартовы прямоугольные координаты

Положение точки в пространстве будем определять относительно пространственной декартовой прямоугольной системы координат, состоящей из трех взаимно перпендикулярных осей координат, пересекающихся в одной точке О, называемой началом координат.

Ось Oxназывают осьюабсцисс, осьOy- осьюординат и осьOz - осьюаппликат.

Координатные оси Ox,Oy,Oz, взятые попарно, определяют три взаимно перпендикулярные плоскостиxOy,yOz,xOz, называемыекоординатными плоскостями.

Декартова система координат позволяет связать с каждой точкой Pпространства, в котором выбраны три не лежащие в одной плоскости направленные прямые Ox, Oy, Oz(оси координат), пересекающиеся в начале O, три вполне определенных действительных числа (декартовы координаты) x, y, z; при этом пишутP(x,y,z).

Оси Ox, Oy, Ozмогут образовывать правую или левую систему. Дляправой системы поворот от осиOxк оси Oyна угол, меньший, совершается в направлении против часовой стрелки, если смотреть на плоскостьxOyиз какой-либо точки положительной полуоси Oz (положительная сторона плоскостиxOy). рис.1.6.

Правая система Левая система

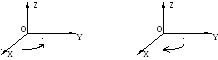
Рис. 1.6

Замечание.Когда мы изучали комплексные числа, то, наряду с декартовой системой координат, рассматривали полярную систему координат на плоскости, которая задается точкойО (полюсом) и полярной осью - лучом, выходящим из полюса. Связь прямоугольных и полярных координат задается формулами:

, где(1.3.1)

1.4. Координатное представление векторов

Пусть мы имеем прямоугольную систему координат в пространстве.

Если вместе с вектором , имеющим произвольную длину, рассмотреть вектор, имеющий единичную длину, но направленный так же, как вектор, то этот вектор называетсяортом вектораи обозначается, например,. Отсюда следует, что.

Обозначим единичные векторы (орты) осейOx, Oy, Ozсоответственно черезпричем.

Разложим произвольный вектор трехмерного пространства по ортам. Для этого построим вектор, равный вектору. Из точкиМ опустим перпендикуляр на плоскость хOу. Из основания этого перпендикуляра (точкаА) опустим перпендикуляры на оси координатОхиОу и соединим точкуАс началомО. На векторахипостроим прямоугольникОАММ₃, диагональю которого будет вектор. Из рис. 1.7 видно, чтоили.

Рис. 1.7

Векторы ,,называютсясоставляющимивектора.

Координаты точек являются координатами вектора.

Можно сказать, что координатами вектора являются его проекции на оси координат.

Составляющие вектора можно выразить через его проекции (координаты):

Подставляя эти значения в равенство и обозначивчерезполучим:

(1.4.1)

Равенство (1.4.1) можно записать в виде:

(1.4.2)

Замечание 1. Равные векторы имеют одинаковые координаты.

Замечание 2. Разложение векторав виде (1.4.1) возможно только единственным способом.

Из единственности разложения (1.4.1) вектора по ортам, следует, что если координаты любых двух векторовиравны, т.е., то эти векторы тоже равны .

Вектор , идущий от начала точкиОк точкеназываетсярадиус - векторомэтой точки, и его координаты совпадают с соответствующими координатами точки(рис. 1.8)

Рис. 1.8

Поэтому , или. Пусть- вектор, координаты начала и конца которого известныи. Тогда координаты векторавыражаются по формулам :

(1.4.3)

Из рис. 1.9 видно, что

(1.4.4)

x

Рис. 1.9

Используя свойства проекций (п.1.2.), имеем: , и аналогичным образом находим.

Разложение вектора по ортам будет иметь следующий вид:

(1.4.5)

Тройка векторов называетсякоординатным базисом, а разложение (1.4.1) вектораназывается разложением векторапо базису.

Замечание. Разложение векторана плоскости по базисуимеет вид.