Дисциплина: “Аналитическая геометрия”

. Элементы векторной алгебры

1.1. Векторы в евклидовом пространстве

В отличие от скалярных величин, которые полностью характеризуются своим численным значением в выбранной системе единиц (температура, работа, плотность и т.д.), векторные величины, кроме численного значения, обладают также направлением в пространстве (например, сила и скорость).

Из школьного курса математики известно, что вектор можно изобразить направленным отрезком, т.е. отрезком прямой, для которого указано какая точка, является началом и какая концом, и при этом указать единицу масштаба (рис. 1.1).

Рис. 1.1

Если точка А начало, аВ конец вектора, то вектор записывается в видеили.

Численная величина вектора называется модулемвектора. Иногда модуль вектора называют его длиной. Модуль, или длина вектора обозначается как ||, ||.

Вектор, у которого начало совпадает с концом, называется нулевым. Векторы, расположенные на прямой или параллельных прямых, называютсяколлинеарными и обозначаются. Векторы, лежащие на параллельных плоскостях или на одной и той же плоскости, называютсякомпланарными.

Два вектора называются равными, если они имеют одинаковый модуль и направление

.

Сложение векторов и умножение на число.

В каждом классе векторов (например, перемещений, скоростей, сил, напряженности магнитного поля) можно определить операции, известные, как сложение векторов и умножение их на число.

Сложение производится либо, используя правило параллелограмма, либо – веревочного многоугольника.

Произведением вектора на числоназывается вектор, определяемый следующими условиями:

1).

2).

3). Векторы иодинаково направлены, если>0, и противоположно - если<0.

Векторы образуют линейное пространство

1). .

2). .

3). , где0- нулевой вектор.

4). , где- противоположный вектор,0 - нулевой.

5). , где,- числа.

6). .

7). .

8). .

Сложение векторов и умножение вектора на число со свойствами 1– 8 называются линейными операциями над векторами.

Рассмотрим векторы на оси. Осью называется прямая на которой выбрано положительное направление. Численным значениемвекторана оси называется число равное длине вектора, взятой со знаком плюс, если направление вектора совпадает с направлением оси, и со знаком минус, если оно противоположно направлению оси. Величина вектораобозначается.

Пример. Пусть длина вектора ||=||=5 . Найти величины этих векторов, если они расположены на осиl , как показано на рисунке 1.2.

= 5,=–5.

Рис. 1.2

Очевидно, что величина суммы двух и большего числа векторов на оси равна алгебраической сумме величин слагаемых векторов.

Пример. Найти величину суммы векторовина оси, (рис.1.3) если ||=3, ||=5 .

Решение.

+=3 + (–5)= –2.

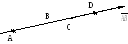
Рис. 1.3

Имеет место утверждение: при любом расположении трех точек на оси величины векторов ,иудовлетворяют соотношению+=(основное тождество).

Доказательство представлено на рис. 1.4, где показаны всевозможные случаи расположения трех точек A,B,Cна осиl.

+=

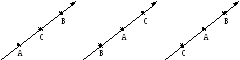
Рис. 1.4