
LS-Sb89585
.pdfМИНОБРНАУКИ РОССИИ
‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒
Санкт-Петербургский государственный электротехнический университет « ЛЭТИ»
‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒‒
ФИЗИЧЕСКИЕ СВОЙСТВА РАДИОМАТЕРИАЛОВ
Методические указания к практическим занятиям
Санкт-Петербург Издательство СПбГЭТУ « ЛЭТИ»
2013
1
УДК 539.2(076)
Физические свойства радиоматериалов: Методические указания к практическим занятиям / Сост.: М. Ф. Ситникова, Е. Ю. Замешаева. Изд-во СПбГЭТУ « ЛЭТИ», 2013. 32 с.
Содержат описания методики решения задач по дисциплине « Основы электроники и радиоматериалы» согласно учебным планам №№ 111-117, 811-814 для бакалавров 4 семестра по направлениям: 210400.62 – « Радиотехника», 210700.62 – « Инфокоммуникационные технологии и системы связи», 211000.62 – « Конструирование и технология электронных средств», и специалистов 210601.65 - « Радиоэлектронные системы и комплексы».
Утверждено редакционно-издательским советом университета
в качестве методических указаний
© СПбГЭТУ « ЛЭТИ», 2013
2
ВВЕДЕНИЕ
Методические указания к практическим занятиям по курсу « Основы электроники и радиоматериалы» предназначены для подготовки бакалавров по направлениям 210400.62 « Радиотехника», 210700.62 « Инфокоммуникационные технологии и системы связи», 211000.62 – « Конструирование и технология электронных средств», 210601.65 « Радиоэлектронные системы и комплексы» ФРТ и для студентов специальности 200800, обучающихся на открытом факультете.
Задача практических занятий – изучение законов квантовой механики и зонной теории твердого тела, физических представлений, лежащих в основе методов разработки элементной базы и технологических процессов микро- и наноэлектроники, а также приобретение навыков анализа физических задач с последующим выбором рационального решения для более глубокого усвоения теоретического лекционного материала, умения производить оценочные и инженерные расчеты физических процессов в твердых телах, грамотного пользования справочной литературой.
В указания включены задачи, позволяющие наряду с достижением вышеуказанных академических целей, проследить динамику взаимосвязи микроструктуры и проявляемых физических свойств основных материалов, используемых в современной радиоаппаратуре, микроэлектронике и соответствующих технологиях производства.
Практические занятия проводятся с использованием программ MCAD, перечисленных в приложениях, и адаптированных специально для решения предлагаемых задач.
ТЕМА 1. ОПИСАНИЕ ОСНОВ СТРУКТУРЫ РАДИОМАТЕРИАЛОВ
Описание структуры радиоматериалов основано на идеях кристаллофизики. Задачи этой темы посвящены описанию структуры кристаллов, индицированию узлов, ребер и плоскостей, изучению симметричных свойств кристаллических структур. Основными методами изучения физических свойств кристаллов являются методы и принципы кристаллофизики.
Особое внимание уделено задаче на определение плотности кристалла, т. к. она является ключевой для расчета концентрации атомов и электронов в кристаллических структурах.
Задача 1.1. Написать формулу симметрии прямой тетрагональной призмы, являющейся одной из решеток Браве.
Для решения задачи необходимо воспользоваться основными положениями описания структуры кристалла.
3
Кристаллическая структура может быть представлена в виде пространственной (кристаллической) решетки (КР), заполненной базисом (одним атомом или совокупностью атомов).
КР – математическая (геометрическая) абстракция, способ представления периодически повторяющихся в пространстве отдельных атомов (совокупности атомов).
Элементарная ячейка КР может быть построена на элементарных трансляциях (базисных векторах) a, b, c так, что все точки определяются радиус-вектором
r = n1a + n2b + n3с , |
(1.1) |
где n1, n2 , n3 – произвольные целые числа.
В зависимости от соотношения модулей базисных векторов, углов между ними и положения узлов все элементарные ячейки можно классифицировать по Браве.
По соотношению между базисными векторами и углами элементарные ячейки и соответствующие кристаллические многогранники подразделяются на три категории – высшую, среднюю и низшую, и 7 сингоний.
Симметричные преобразования над кристаллическим многогранником образуют точечную группу и объединяются в класс симметрии.
Все элементы симметрии данного класса могут быть записаны формулой симметрии: например, для куба, имеющего 6 поворотных осей 2-го порядка, 4 поворотные оси 3-го порядка, 3 поворотных оси 4-го порядка, 9 плоскостей симметрии и центр инверсии, формула симметрии выглядит как 3L4 4L3 6L29PC .
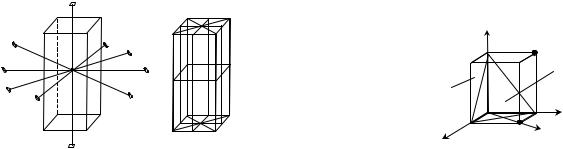
Рассматривая симметрию прямой тетрагональной призмы, выявляем наличие осей 2-го, 3-го, 4-го и 6-го порядка (рис. 1.1), возможных в твердом теле. В нашем случае есть четыре оси L2, ось L4, нет осей 3-го и 6-го поряд-
ка. Кроме того, у тетрагональной призмы есть горизонтальная плоскость симметрии P1, два семейства вертикальных взаимно перпендикулярных плоскостей симметрии P2, P3 и P4, P5 и центр симметрии.
L4 |
P2 |
P4 |
P3 |
|
|
|
|
|
P5 |
|
|
[001] z |
[[011]] |
||
|
|
|
|
||||
|
|
|
|
|
|
||
C |
|
|
P1 |
|
|
|
(111) |
|
L2 |
|
|
|
|
||
|
|
|
(010) |
|
|
y [010] |
|
|
|
|
|
|
|
|
|
|
|
|
|
[100] x |
|
[[110]] |
[110] |
|
|
|
|
|
|
|
|
|
Рис. 1.1 |
|
|
|
Рис. 1.2 |
|
|
4
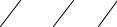
Задача 1.2. Найти индексы плоскости, отсекающей по кристаллографическим осям отрезки 9, 10, 30, если базисные векторы а = 3, b = 5 и с = 6.
Для индицирования (описания) узлов, направлений и плоскостей в кристаллах используют индексы (см. рис. 1.2.).
Если r – радиус-вектор, проведенный из начала координат в рассматриваемый узел, то индексами узла будет совокупность чисел n1, n2, n3 в
уравнении (1.1), записываемая [[n1, n2 , n3 ]].
За индексы направления ребра принимаются индексы ближайшего к началу координат узла, через который проходит рассматриваемое направление, проведенное из начала координат [n1, n2 , n3 ] .
Индексы Миллера для плоскости представляют собой коэффициенты в уравнении плоскости, написанном в параметрическом виде; для нахождения индексов Миллера следует:
а) выразить отрезки, отсекаемые плоскостью на осях координат, через базисные отрезки (векторы) a, b и с;
б) найти обратные значения этих величин, привести их к виду наименьших возможных рациональных дробей, имеющих общий знаменатель;
в) отбросить общий знаменатель и заключить полученные три числа в круглые скобки (h k l ).
В нашей задаче действуем согласно указанному правилу:
а) выразим отрезки, отсекаемые плоскостью на осях координат, через базисные векторы:
n |
= |
9 |
= 3; n |
= |
10 |
|
= 2; n |
= |
|
30 |
= 5; |
|||||||||
|
|
|
|
|
|
|||||||||||||||
1 |
3 |
2 |
5 |
|
|
|
3 |
6 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
б) найдем обратные числа: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
= |
1 |
; |
1 |
= |
1 |
; |
1 |
= |
1 |
; |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
n1 3 |
n2 2 |
n3 |
5 |
|
|
||||||||||||
в) приведем их к наименьшему общему знаменателю:
1030 ; 1530 ; 630
и отбросим знаменатель. Полученные числа есть индексы Миллера иско-
мой плоскости (h k l) = (10, 15, 6).
Задача 1.3. Записать матричное представление оси второго порядка, параллельной оси Z.
Преобразования симметрии в кристаллическом пространстве описываются как соответствующие преобразования координат (рис.1.3).
5
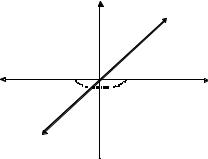
Точка с координатами x, y, z после преобразования симметрии займет новое положение с координатами x′, y′, z′, определяющимися уравнениями преобразования:
x′ = c11x + c12y + c13z,
y′ = c21x + c22y + c23z,
z′ = c31x + c32y + c33z,
где ci, j – косинусы углов между осями координат; i, j = 1, 2, 3.
|
Z |
|
|
|
Z' |
|
Любому |
преобразованию симметрии |
|||||
|
|
|
|
||||||||||
|
|
|
|
|
X' |
|
можно поставить в соответствие матрицу пре- |
||||||
|
M'(x',y',z'’) |
|
|
|
M(x,y,z) |
|
образования ∆i,j, элементами которой являют- |
||||||
|
|
|
|
|
ся косинусы углов ci,j: |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
Y' |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Y |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
11 |
12 |
|
13 |
||
|
|
|
|
|
|
|
|
|
c |
|
|
|
. |
|
X |
|
|
|
|
|
i = |
21 |
22 |
|
23 |
|
|
|
|
|
|
|
|
, |
|
|
|
||||
|
|
|
|
|
|
|
j |
|
c c |
|
c |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Рис. 1.3 |
|
Требуемое |
|
31 c |
32 c |
33 |
|
|||||
|
|
|
|
|
|
|
симметричное |
преобразова- |
|||||
ние представляет поворот кристаллографических координат вокруг оси L2
(оси Z) на угол 180°. Введем новую систему координат x′, y′, z′, связанную с исходной x, y, z следующими соотношениями:
x′ = cos(xx′)× x = cos(π × x = (-1)× x, y¢ = cos(yy¢)× y = cos(π )× y = (-1)× y, z¢ = cos(zz¢)× z = cos(0)× z = (+1)× z.
Соотношения между разноименными осями (например, xy′) определяются косинусами углов, равных 90° ( все разноименные оси взаимно перпендикулярны), поэтому искомое преобразование симметрии следует записать в виде матрицы:
(
L | |
Z |
|
- 1 |
0 |
0 |
|
= |
|
|
- 1 |
|
||
2 | |
|
|
0 |
0 . |
||
|
|
) |
|
0 |
0 |
|
|
|
|
1 |
|||
Задача 1.4. К кубическому кристаллу с симметрией m3m приложили одноосное напряжение растяжения вдоль оси L4. Какой сим-
метрией будет обладать кристалл?
Взаимосвязь физических свойств кристаллов и симметрии их структуры описывается принципами кристаллофизики.
Принцип Неймана: группа симметрии любого физического свойства кристалла должна включать в себя группу симметрии кристалла.
6
Для описания симметрии физических свойств и внешних воздействий служат предельные группы симметрии (группы Кюри), содержащие оси бесконечного порядка.
Принцип суперпозиции Кюри: кристалл, находящийся под влиянием внешнего воздействия, будет обладать теми элементами симметрии, которые являются общими для воздействия и кристалла в отсутствие воздействия. Свойства кристалла, связывающие воздействия явления, можно отобразить схемой:
явление (эффект) = (свойство) × ( воздействие). (1.2)
По условию задачи растягивающее напряжение приложено по оси L4
вдоль направления [0 0 0]. Симметрия приложенного воздействия соответствует предельной группе ∞/mmm с геометрическим образом в виде покоящегося цилиндра вращения.
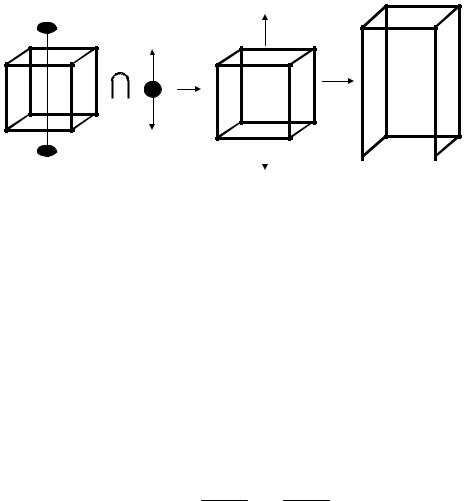
Применяя принцип суперпозиции Кюри (1.2), найдем общие элементы для кристалла в отсутствие воздействия и воздействия в отсутствие кристалла (рис. 1.4).
L4[001]
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m3m |
mmm |
|
|
|
4 |
|
|
|
|||||||
|
|
|
|
|
|
mmm |
|
|
|
Рис. 1.4 |
|||||
Общими элементами симметрии будут ось L4, четыре вертикальные плоскости, проходящие параллельно L4, одна перпендикулярная оси L4 го-
ризонтальная плоскость, четыре оси L2 на пересечении вертикальных плос-
костей с горизонтальной плоскостью и центр инверсии.
Полученная симметрия соответствует симметрии тетрагональной призмы 4/mmm.
В аналитическом виде схеме (1.2) соответствует операция перемножения матрицы симметрии кристалла и матрицы предельной группы, соответ-
ствующей данному физическому воздействию, т. е.: |
||||||
m3 m |
|
∞ |
|
= |
4 |
|
) |
|
|
|
|
|
|
|
|
m |
m |
|||
× |
m |
|
|
m |
. |
|
|
|
|
|
|
||
|
|
m |
|
|
m |
|
7

Задача 1.5. Определить постоянную решетки кристалла NaCl; плотность кристалла ρ = 2,18·103 кг/м3.
Плотность вещества зависит от типа структуры, плотности упаковки, атомной массы. С увеличением плотности упаковки возрастает и плотность
вещества (кристалла). Плотность кристалла ρ связана формулой |
|
||||
ρ= |
V= |
V× |
N |
|
(1.3) |
× |
|
||||
|
|
|
|
|
|
с его относительной массой A, объемом элементарной ячейки V, числом атомов N в элементарной ячейке (NA – число Авогадро).
В кристалле NaCl можно выделить ячейку в виде куба, в вершинах которого поочередно находятся атомы Na и Cl. Ребро куба d, объем d 3. Такая ячейка содержит 1/2 атома Na и 1/2 атома Cl. Если атомный вес ANa = 23, ACl = 35,46 , то масса выделенной ячейки определяется из выра-
жения (1.3): |
M m N A |
|
N A ρ d , m N |
|
|
|
|||||||||
|
|
|
|
|
|||||||||||
|
= |
H |
N |
N |
+ |
|
C |
C |
3 |
H |
− |
, |
|
||
|
( |
a × |
a |
|
l × |
l ) = |
|
|
= |
|
|
||||
где m – масса атома водорода, m |
H |
= 1,66·10–27 |
кг; N |
Na |
и N |
Cl |
– число ато- |
||||||||
H |
|
|
|
|
|
|
|
|
|
|
|
|
|||
мов Na и Сl соответственно в выбранной ячейке. Разрешая формулу относительно d, получим:
|
|
|
|
|
|
|
|
|
1,66 ×10−27(23 + 35,6) |
|
|
|
||
|
|
m |
1 |
(A |
+ A ) = 3 |
|
|
×10−10м. |
||||||
d = 3 |
H |
× |
|
|
|
|
|
= 2,8 |
||||||
|
|
|
|
|
|
|||||||||
|
|
ρ |
2 |
|
Na |
Cl |
2,18 |
×103 ×2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
Постоянная решетка кристалла определяется расстоянием между двумя одинаковыми атомами, т. е. a = 2d = 5,62Å.
Примечание. Применение соотношения (1.3) может быть полезным при оценке концентрации электронов n в кристаллах металлов по известной концентрации атомов N и валентности Z: n = NZ.
ТЕМА 2. ДИНАМИКА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ. ТЕПЛОЕМКОСТЬ РЕШЕТКИ
Тепловые и механические свойства материалов, применяемых в радиоэлектронике, определяются движением атомов кристаллов за счет теплового или механического возмущения, описание которого представляет довольно сложную задачу. В предлагаемом разделе рассматриваются задачи с использованием различных моделей-приближений: модели изолированного атома, модели Дебая, одномерной цепочки атомов. Основными физическими задачами являются задачи определения скорости звука, теплоемкости и спектра фононов радиоматериалов. Для их решения студенты могут воспользоваться программой MCAD (П4 в списке прил.).
8

Задача 2.1. Определить частоту колебания атомов кристалла меди, используя модель изолированного атома.
Простейшей моделью, описывающей движение атома, является модель изолированного атома, в которой атом рассматривается в виде точечной массы m, закрепленной на пружинных связях относительно неподвижных опор (соседних атомов).
В гармоническом приближении, в случае изотропной кубической решетки потенциальную энергию V(u) как функцию малого смещения атома u из положения равновесия можно записать
V (u) = 1β× u2,
2
где β – параметр упругости материала (жесткость связей). Соответствующая сила, противостоящая смещению атома из положения равновесия:
F(u) = - dV (u) = -β× u. du
Смещение атома из положения равновесия в зависимости от времени t |
|
|||||
u |
As |
ω t, |
ω |
β m |
|
|
= |
0 i |
0 |
0= |
|
(2.1) |
|
|
, |
|||||
|
n |
|
|
|
|
|
где ω0 – частота собственных колебаний атома массой m. |
|
|||||
Параметр упругости материала в рамках закона Гука (механическое |
||||||
напряжение пропорционально относительной деформации) определяется выражением:
β = 4aY, |
(2.2) |
где a – параметр решетки; Y – модуль Юнга.
Для кристалла меди находим значение необходимых параметров a, Y, ACu (прил. 1). Используя соотношения (2.1) и (2.2), находим значение часто-
ты колебаний атомов при заданных допущениях: |
|
|
|||||||||||||
|
|
|
β |
|
|
|
|
|
|
|
|
|
|||
ω0 |
|
|
|
|
|
|
= |
|
4 ×3,61×10−101,15 ×1011 |
|
|
||||
= |
|
|
|
|
= |
|
4aY |
|
|
|
= 4 ×1013c−1. |
||||
m |
ACumH |
63,5 ×1,67 ×10−27 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
Задача 2.2. Определить скорость звука в кристалле меди, используя модель Дебая для описания спектра акустических фононов.
Для изотропных кристаллов при описании спектра акустических фононов можно воспользоваться решением, полученным для одномерной цепочки одинаковых масс m, связанных упругими связями β с соседними фононами. Дисперсионное уравнение, связывающее частоту колебаний ω и
волновой вектор k (рис. 2.1.а), имеет вид: |
|
|
|
|
||||||
ω |
|
|
β |
|
|
|
|
|||
|
|
|
|
|
ka |
|
|
|||
= 2 |
× |
|
|
|
× |
sin |
|
|
, |
(2.3) |
m |
|
|||||||||
|
|
|
|
|
|
2 |
|
|
||
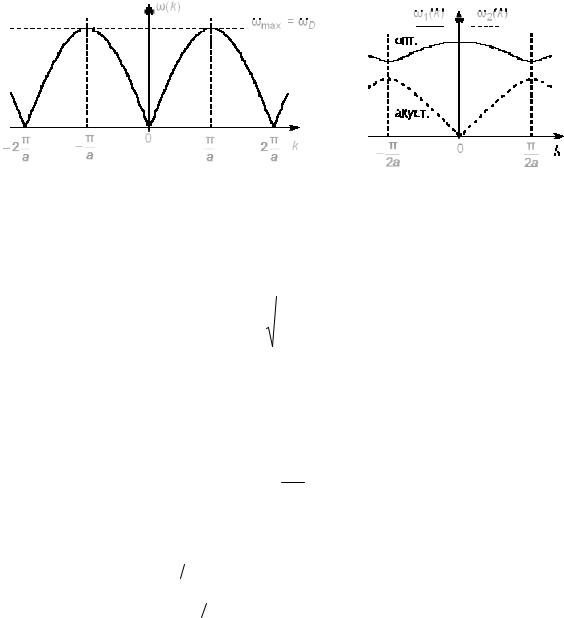
где k = 2π/λ – модуль волнового вектора k; λ – длина волны упругих смещений атома; a – постоянная решетки.
Область значений волнового вектора, для которой не возникает неоднозначности дисперсной кривой ω(k), называется зоной Бриллюэна.
а |
б |
Рис. 2.1
Для одномерной цепочки из 2-х видов атомов с массами m и M (M > m) дисперсионное уравнение
ω |
|
β |
|
1 |
|
1 |
|
|
1 |
|
1 2 |
4sin2 (ka) |
|
|
||||
2 |
= |
2 |
|
|
+ |
|
|
± |
|
|
+ |
|
|
− |
|
|
|
(2.4) |
1,2 |
|
|
|
|
|
mM |
||||||||||||
|
|
m M |
|
m M |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеет две ветви (рис. 2.1.б). Нижняя ветвь (минус перед корнем в (2.4) соответствует акустическим колебаниям, верхняя ветвь (плюс перед корнем в (2.4) – оптическим колебаниям.
Для цепочки из N атомов число допустимых значений модуля волново-
го вектора kS в зоне Бриллюэна: kS = 2π S; S = 0, 1, 2, ..., N - 1.
Na
Полная сумма волн с различными kS, описывающая движение n-атома
в составе цепочки: |
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
(N 2)−1 |
|
|
ω |
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||
un = |
|
|
∑ |
AS exp i |
S t - |
|
|
S ×n , |
|
||||||||
|
|
|
|
|
|||||||||||||
|
S=−N 2 |
|
|
|
|
|
N |
π |
|
|
|
(2.5) |
|||||
|
1 |
|
N −1 |
|
|
|
ω |
|
2 |
S n |
. |
||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
∑ u |
|
|
|
N |
|
|
|
||||||||
A = |
|
|
|
n |
exp |
- i |
S |
t - |
|
× |
|
|
|
||||
|
|
|
|
|
|
|
|||||||||||
S |
|
N n=0 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Каждая из бегущих волн по цепочке (2.5) представляет собой независимый осциллятор с частотой колебаний ωS и амплитудой AS, не завися-
щей от амплитуды других волн. Ортогональные волны цепочки называются нормальными колебаниями. Квант нормальных колебаний кристаллической решетки – фонон – квазичастица с энергией ES = ħωS и квазиимпульсом pS = ħkS (ħ – постоянная Планка, ħ = h/2π).
10
