
LS-Sb89585
.pdf
В модели Дебая вместо сложной зависимости ω(k) (2.3), (2.4) принимается линейная аппроксимация (см. рис. 2.1.б)
ω (k) = vзвk, (2.6)
что хорошо описывает зависимость ω(k) на низких (звуковых) частотах. Скорость звука vзв в этом случае находится из соотношения (2.6) по
известной максимальной частоте акустических фононов – частоте Дебая (ωmax = ωD) и соответствующему максимальному значению волнового век-
тора kmax, при этом модуль вектора kmax определяется как
kmax = 2 min = |
, min = 2a . |
Частоту Дебая ωD находят обычно по известной характеристической |
|
температуре Дебая TD из соотношения: |
|
= |
. |
Окончательно для скорости звука (скорости акустических фонов по модели Дебая) получаем:
|
D |
|
kБTD a |
|
зв = |
|
= |
π |
. |
kmax |
|
|||
|
|
|
||
Используя соотношения (2.7) и данные для меди, находим: |
||||||||||
|
1 |
1 |
− 3 |
|
3 |
3 |
1 |
− 0 |
4 |
1 3 |
з |
, |
× 0 |
× |
1 |
× , |
× 0 |
||||
в = |
3 |
3 |
1 |
5 |
16 |
3 |
|
= , |
× 0 м/с. |
|
|
8 |
, |
× |
, |
|
- |
4 |
|
7 |
|
|
|
× 01 |
|
|
|
|||||
|
|
1 |
0 |
|
|
|
|
5 |
|
|
Задача 2.3. Определить число оптических фононов |
||||||||||
|
|
4 |
5 |
|
|
|
|
|
|
|
(2.7)
в кремнии
при T = 300 К; энергию возбуждения оптических фононов считать
равной энергии Дебая ( = |
= п |
|
= |
|
). |
|||
Среднее число фононов с энергией |
|
|
= |
|
определяется распреде- |
|||
лением Планка: |
ωn ) = |
|
|
|
|
|
|
|
f (En ) = f ( |
|
|
|
1ω |
|
|
, |
|
|
n |
|
||||||
|
|
|
|
|
|
-1 |
||
|
|
|
|
|
||||
|
|
exp k T |
|
|||||
|
|
|
|
|
Б |
|
|
|
где kБ – постоянная Больцмана; T – температура кристаллической решетки.
При |
>> (случай высоких температур) |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
Б |
|
|
Б |
|
T |
|
|
|
|
|
||
|
|
|
|
f (ωn ) = |
|
ω |
= |
|
|
ω |
= |
. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для нашего случая среднее число фононов с энергией |
|
|
|||||||||||||||||
|
|
|
ω |
ω |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
N( D ) = f ( D ) = |
|
|
ω |
|
= |
|
|
. |
||||||||||
|
|
|
|
T |
|||||||||||||||
|
|
|
|
|
|
|
|
D |
|
-1 |
|
exp |
D |
|
-1 |
||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
exp |
kзT |
|
|
|
T |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
11

При TD > T имеем N(ωD ) = exp(−TD 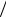 T ) = exp(− 625
T ) = exp(− 625 300) ≈ 0,135 < 1, т. е. опти-
300) ≈ 0,135 < 1, т. е. опти-
ческие фононы в Si при 300 K не возбуждаются.
Задача 2.4. Найти векторы обратной решетки для ромбоэдрического кристалла кальция, если a = 5,36 Å, α = 46°.
Для описания свойств волнового вектора служит обратное пространство (или пространство волнового вектора). Связь обратного пространства (обратной решетки) с конфигурационным пространством (прямой решеткой) осуществляется соотношениями
|
2π |
[b × c], b* = |
2π |
[c × a], c* = |
2π |
[a × b] |
|
|
a* = |
|
|
|
(2.8) |
||||
V |
V |
V |
||||||
|
|
|
|
|||||
V = a[b × c], |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
где a*, b*, c * – базисные векторы обратной решетки; a, b, |
c – базисные |
|||||||
векторы прямой решетки; V – объем элементарной ячейки; a, b, c и a*, b*, c*
–модули базисных векторов прямой и обратной решеток соответственно.
Вромбоэдрической ячейке a = b = c, α = β = γ. Следовательно, согласно (2.8), a* = b* = c*, α* = β* = γ* (углы между базисными векторами обратной решетки).
Объем элементарной ячейки |
|
|
α |
|
|
|
|
α |
|
|
|||||||||
|
|
V = a[b × c] = a3 |
1− 3cos2 |
|
|
|
|
|
3, |
||||||||||
|
|
+ 2cos3 |
= 121 (Å) |
||||||||||||||||
|
|
|
|
|
a* |
a s |
α |
V |
0 |
|
|
|
–1, |
|
|
||||
с α |
c |
α |
c α |
= |
|
i |
c |
= |
, |
|
(Å) |
|
0 |
; α 1 5 |
|||||
s α n |
|
α 21 |
c α |
||||||||||||||||
o * |
= ( o |
− |
o |
) |
i |
|
= − |
o |
|
(4 |
+ |
o |
|
|
) = − |
, |
* = 1 ° ′ . |
||
s |
s |
|
s |
|
n |
|
|
|
|
s |
|
|
|
s |
|
|
|
4 |
4 |
Задача 2.5. Определить теплоемкость кристалла меди, погру- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
женного в криостат с жидким гелием. |
|
|
|
|
|
9 |
|
||||||||||||
Теплоемкость твердых тел при высоких температурах описывается за- |
|||||||||||||||||||
коном Дюлонга–Пти (классическая модель): |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
C |
|
d E |
|
3 k N |
|
3 R, |
|
|
||||||
|
|
|
|
|
V |
|
d |
|
T |
|
|
Б |
A |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
= |
|
|
|
= |
|
|
|
|
(2.9) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где R – универсальная газовая постоянная.
Согласно модели Дебая, теплоемкость решетки, в которой могут рас-
пространяться колебания с частотами от 0 до ωD без дисперсии: |
|
||||||||||||||
|
C |
9 k N |
T |
3 |
TD |
T |
|
x4 e4 |
|
|
d x, |
|
|||
|
V |
Б 0 |
T |
|
|
|
|
|
|
x |
|
2 |
|
|
|
|
= |
|
|
× |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
∫ |
( |
e |
|
1 |
|
|
|
||||||
|
|
|
D |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
− |
|
|
|
|
|||
где TD = ωD kБ – |
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
температура Дебая; |
ωD – частота Дебая, |
соответст- |
|||||||||||||
вующая волне минимальной длины ( |
i |
= |
), |
распространяющейся по |
|||||||||||
решетке; x = (kБ |
) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12

Случай высоких температур (T >> TD) соответствует (2.9). В случае низких температур (T << TD)
CV = 234R(T TD )3 . |
(2.10) |
Температура Дебая меди TD = 315 K много больше заданной темпера-
туры эксперимента THe = 4,2 K. Следовательно, для области низких темпе-
ратур справедлива формула определения теплоемкости (2.10), и тогда
|
4,2 |
3 |
Дж |
|
||||
C = 234 × 8,31 |
|
|
|
= 4 ×10−3 |
|
|
. |
|
|
|
|
||||||
V |
315 |
|
|
К ×моль |
|
|||
|
|
|
||||||
ТЕМА 3. СТАТИСТИКА ЭЛЕКТРОНОВ ТВЕРДОГО ТЕЛА
Для характеристики состояния в твердом теле большого числа частиц и квазичастиц, таких как электроны, фононы, дырки, атомы примеси и пр., используют классические и квантовые статистические распределения – статистику Больцмана для классических частиц, статистику Планка для фононов, статистику Ферми–Дирака для электронов и дырок в вырожденном состоянии.
Задачи этой темы способствуют формированию навыков правильного выбора и использования статистики для описания свойств частиц в заданных состояниях, главным образом электронов и дырок в металлах и полупроводниках. Для анализа состояния электронов и дырок студенты могут воспользоваться программой MCAD (П5 в списке прил.).
Задача 3.1. Определить состояние электронного газа в кристалле кремния (n = 1019 м–3 , m* = 0,7m0) в диапазоне температур
T = 77 ... 300 K.
Состояние электронного газа в кристалле может быть вырожденным, т. е. описываться распределением Ферми–Дирака для системы квантовых частиц с полуцелым спином и химическим потенциалом, равным энергии
Ферми EF: |
( ) ( ) |
|
|
k T |
|
|
|
|
|||||||
|
|
|
N |
n |
En= |
f En= |
|
|
|
E |
E |
|
|
, |
(3.1) |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
n |
F |
|
|||||
|
|
|
|
|
|
|
|
e |
|
1 |
|
||||
|
|
|
|
|
|
|
|
− |
|
|
|
||||
|
|
|
|
|
|
|
|
x |
|
Б |
|
|
+ |
|
|
|
N |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где – среднее число частиц в соответствии с энергией En при темпера-
туре T; f(En) – функция распределения частиц по состояниям с энергией En .
Если kБT > EF для любого En , то (3.1) переходит в распределение для идеального газа электронов (дырок), которое называется невырожденным и
13

описывается распределением Больцмана по состояниям с энергией En для
системы классических невзаимодействующих частиц: |
|
|||||||||||
|
f En |
|
e |
μ |
En |
A e |
|
- |
En |
|||
|
|
-k T |
|
k T |
||||||||
|
|
= |
x |
|
Б |
|
|
= × x |
|
|
Б |
, |
|
|
|
|
|
|
|
|
|||||
|
( ) p |
|
|
|
|
p |
|
|
|
|
||
где = x ( |
); µ – химический потенциал. |
|
|
|
|
|||||||
Вырожденный электронный газ характеризуется значением параметров Ферми и прежде всего значением энергии Ферми EF.
Изоэнергетическая поверхность в k-пространстве с энергией E = EF
называется поверхностью Ферми. Для свободного электронного газа с концентрацией электронов n и эффективной массой m* поверхность Ферми – сфера с радиусом kF, при этом
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
k |
|
|
( |
π |
n |
) |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
E |
|
= |
|
|
kF |
, |
= |
3 |
|
2 |
1 |
3 . |
|
|
|
|
(3.2) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
F |
|
|
2m * |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для оценки степени вырождения электронного газа вычисляем энергию |
||||||||||||||||||||||||||||
Ферми (3.2): |
( |
π |
|
n |
|
|
|
|
|
1 |
|
1 |
|
) ( |
3π |
|
|
1 |
) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|||||||||||||
EF |
|
2 |
|
) |
|
(0 |
|
0− 4 |
|
|
|
|
, |
−21 |
|
|||||||||||||
2 3 |
|
|
2 3 |
|
|
|
|
, |
× |
|
|
|
|
× |
|
0 1 / |
|
|
||||||||||
|
|
|
|
m * |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||
= |
|
2 |
|
|
|
|
|
= |
|
|
|
|
|
2 0 9 1 |
|
|
1 |
|
= 3 8 |
×10 |
|
Дж |
||||||
|
|
|
|
|
|
|
|
|
|
5 |
|
× , |
|
× |
, |
× |
0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
и тепловую энергию в заданном диапазоне температур EТ: |
|
|
|
|||||||||||||||||||||||||
при Т = 77 К E |
Т |
= k Т = 1,38·10–23·77 = 1,06·10–21 Дж < 3,8·10–21 Дж, |
||||||||||||||||||||||||||
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
при Т = 300 К |
E |
Т |
= k Т = 1,38·10–23·300 = 4,14·10–21 Дж > 3,8·10–21 Дж. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя критерий вырождения, в нашем случае для заданной концентрации электронов при Т = 77 К имеем слабо вырожденный электронный (дырочный) газ, который при повышении температуры до 300 К становится вырожденным и описывается распределением Ферми–Дирака (3.1).
ТЕМА 4. ЭНЕРГЕТИЧЕСКИЙ СПЕКТР ЭЛЕКТРОНОВ В КРИСТАЛЛЕ (ЗОННАЯ СТРУКТУРА)
Для описания поведения электронов в кристалле воспользуемся вероятностными законами квантовой механики и так называемым квазиклассическим приближением. Критерием выбора является соотношение между длиной волны де Бройля для частицы λБр и характерным геометрическим размером системы, например, постоянной решетки a.
Соотношение де Бройля сопоставляет свободную частицу с энергией E
и модулем импульса p, а также волну с частотой ω и длиной волны λБр: |
|
|||||
λ |
|
p |
m |
|
. |
(4.1) |
|
|
|
||||
Бр = = |
v |
|||||
|
|
|
|
|
||
14

Если λБр становится соизмеримой с a, частица описывается законами
квантовой механики. В этом случае движение частицы определяется вол- |
||||
новой функцией Ψ(r,t), которую находят из уравнения Шредингера |
||||
i d (r,t ) |
ˆ |
ψ r |
||
× |
|
|
= H |
( ,t ), |
|
||||
dt
где Ĥ – оператор полной энергии.
Для характеристики частицы в пространстве необходимо решить уравнение Шредингера
2 |
Ψ |
|
|
|
Ψ (r) + [E -V (r)] |
(r) = 0 |
(4.2) |
|
|||
2m |
|
|
|
и найти энергетический спектр, т. е. зависимость энергии частицы от волнового вектора k – волновой функции Ψ(r).
Задача 4.1. Найти длину волны де Бройля для электронов, если ускоряющее напряжение в электронном микроскопе равно 50 В.
Для частицы в ускоряющем электрическом поле с потенциалом V соот-
ношение (4.1) переходит в соотношение |
|
|
|
||
λрБ = |
|
|
|
|
. |
|
|
|
|
||
|
e |
||||
2 |
|
|
|||
Тогда для свободного электрона с массой m0 и зарядом e имеем:
λ |
6,62 |
×10 |
−34 |
|
|
×10−10 м–1. |
||
Бр = |
|
|
|
= 1,65 |
||||
|
|
|
|
|
||||
2 ×9,1×10−31 ×1,6 ×10−19 ×50 |
||||||||
|
|
|
|
|
||||
Задача 4.2. Найти энергетический спектр E(k) и волновую функцию Ψk(r) для свободных электронов.
Для свободной частицы V(r) = 0 и уравнение Шредингера (4.2) имеет
вид |
|
|
|
|
|
|
|
|
|
|
|
Eψ |
0 |
|
|
|
|
2 m |
ψ (r) |
+ (r) = |
. |
(4.3) |
|
|
|
|
|
||||
Решением уравнения (4.3) для свободных электронов является плос- |
|||||||
кая волна де Бройля |
( ) |
|
× . |
|
|
|
|
Ψ r = eA- |
|
|
|
||||
Энергия свободных электронов связана со значениями модуля волнового вектора k параболической зависимостью
E(k ) = 2k2 . 2m0
Задача 4.3. Определить вид энергетического спектра для электронов в одномерной потенциальной яме с бесконечно высокими
15
стенками и плоским дном. Найти энергию второго квантового состояния, если ширина ямы a = 5Ǻ, m = m0.
Для частицы в одномерной потенциальной яме с бесконечно высокими стенками и плоским дном из решения (4.2) находим:
|
|
|
|
|
|
|
|
En = |
2k2 |
, |
kn |
= n |
, |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где n – любое положительное целое число. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Для n = 2 получим |
2 π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 2 |
2 |
|
|
|
|
|
|
|
|
3 |
|
2 |
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
k |
|
|
|
|
|
a |
|
|
|
|
1 |
|
1 |
|
|
|
|
|
4π |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||||
E2 |
2 |
|
|
|
|
|
|
|
, |
× |
03− |
4 |
|
|
|
1 2 |
|
1 |
|
|||||||||
2 m |
|
|
|
2 m |
|
|
|
|
|
|
|
|
|
− 8 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
0 |
= |
|
0 |
|
= |
2 |
(9 |
0 |
1− |
|
|
|
)5 1− |
|
= |
0 |
Дж. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
× |
3 |
|
5 |
0 |
( |
× 0 |
0 |
) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
, |
|
× |
1 × |
|
|
|
|
|
|
|
|
|
||||||
Задача 4.4. В приближении слабой1 связи определить концентрацию электронов в кубических кристаллах из условия касания сферы Ферми и зоны Бриллюэна в обратном пространстве (a = 3Ǻ).
Потенциальное поле кристалла V(r) можно аппроксимировать повторяющимися с периодом a потенциальными барьерами заданной высоты. Решение уравнения Шредингера (4.2) в этом случае приводит к зависимости E(k) в виде повторяющихся разрешенных (РЗ) и запрещенных (ЗЗ) зон значений энергии электронов (рис. 4.1).
E |
|
ky |
|
|
π/a |
|
|
зз |
|
|
|
|
|
kБр |
|
рз |
|
kF |
|
-π/a |
π/a |
||
зз |
|
kx |
|
-2π/a -π/a 0 π/a 2π/a k |
|
|
|
|
-π/a |
|
|
Рис 4.1 |
|
Рис 4.2 |
|
Функция E(k) имеет разрывы в точках, где k ‒ модуль волнового векто-
ра k, равен ks = ±S a (S – положительное целое число) и описывается вы-
ражением
E(k ) = 2k 2 . 2m
Для изотропных кристаллов кубической сингонии зона Бриллюэна представляет собой куб со стороной 2π/a. Для 1-й зоны Бриллюэна (s = 1) kБр = ±π/a (рис. 4.2).
Поверхность Ферми для слабо связанных (свободных) электронов есть сфера, радиус которой kF связан с концентрацией электронов n зависимо-
16

стью |
kF = (3π2n)1/ 3 . |
Из |
|
|
|
условия |
|
kF |
= kБр = |
|
|
получаем |
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
n |
|
|
|
|
|
|
4 1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
|
3 a3= |
3× |
3 1 |
1 3» × 0 |
8 м–3. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
( |
× |
0− |
0 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 4.5. |
Определить групповую скорость электронов на по- |
||||||||||||||||||||||||
верхности Ферми, если m* = 0,1m ; k |
F |
= 1028 м–1 . |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Групповая скорость электронов в кристалле определяется соотношением |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
рг = |
|
|
|
|
|
|
= |
|
. |
|
|
|
|
|
(4.4) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Для нашего случая k = kF и групповая скорость электрона на поверхно- |
|||||||||||||||||||||||||
сти Ферми равна скорости Ферми |
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
vF |
k |
|
|
|
× |
|
|
|
|
|
1 7 |
|
|
|
|||||
|
|
|
|
|
г |
|
F |
|
, |
|
|
0 − 4 × |
0 |
0 |
|
|
|
|
||||||||
|
|
|
|
|
р = |
|
= |
m*= |
|
0 |
9 |
× |
|
1 |
3 |
|
0 |
|
= |
0 м/с. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
, |
|
0 |
− 1 × |
, |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
Задача 4.6. Указать правильное соотношение между эффектив-
ными массами электронов в состояниях с модулями волновых векторов kA, kB для заданного энергетического спектра E(k) (рис. 4.3).
Рассматриваемый энергетический спектр E(k) имеет три ветви: вырожденные E1(k) и E2(k) и двухдолинный E3(k). Поведение электронов в кри-
сталле описывается с помощью
E
E3(k)
kA |
kB |
E2(k) k
эффективной массы m*, определяемой вблизи экстремальных точек функции
E(k) как:
* |
|
|
2 |
) |
|
|
|
|
|
dk ( |
|
. |
(4.5) |
||
m = |
d2 E k |
|
|
||||
|
|
||||||
|
|
|
|
||||
|
|
2 |
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для изотропного кристалла эффективная масса m* – скалярная величина. В общем случае необхо-
димо использовать тензор обратной эффективной массы. Из (4.5) следует, что эффективная масса прямо пропорциональна радиусу кривизны
функции E(k). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В нашем случае для вырожденных ветвей согласно (4.5) имеем |
|
|
|
|||||||||||||||||||||||||
|
* |
|
|
|
|
2 |
* |
|
|
|
|
2 |
|
|
d |
2 |
E1 |
|
|
|
d |
2 |
E2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
m |
1 kA = |
|
|
|
|
< m 2 kA = |
|
|
|
, т. к. |
|
|
|
> |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
dk 2 |
|
|
dk 2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
( |
) |
|
d2E1 |
k |
|
( |
) |
|
d2E2 |
|
|
|
k |
|
|
|
k |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
dk 2 |
|
|
|
|
dk 2 |
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
A |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
k A |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
17
и m*1(kA) < 0, m*2(kA) < 0, т.е. для выпуклых экстремумов E(k) мы определя-
ем эффективную массу дырок. Для двухдолинной ветви E3(k), используя
(4.5), получаем
m*3(kA) < m*3(kB); m*3(kA) > 0; m*3(kB) > 0,
т. е. в первой долине при k = kA электроны более легкие, чем во второй долине при k = kB.
ТЕМА 5. КИНЕТИЧЕСКИЕ ЯВЛЕНИЯ В ТВЕРДЫХ ТЕЛАХ
Для качественного описания кинетических явлений используют элементарный кинетический метод, в котором носители электрического заряда электроны (дырки) и носители тепла фононы рассматриваются как свободные частицы, при этом расчет ведется по отношению к одной частице, движущейся свободно между двумя последовательными столкновениями с различными рассеивающими центрами, с последующими усреднением по всем частицам. Согласно этой теории с учетом квантовых представлений, определяющих эффективную массу носителя заряда m", для электропроводности твердых тел пользуются выражением:
σ = |
e2n0τ |
, |
(5.1) |
|
|||
|
m" |
|
|
где: n0 - концентрация электронов; τ – время свободного пробега электрона
(время релаксации). Электропроводность материала может быть вычислена также по формуле
σ = enµ,
где использовано соотношение между средним временем свободного пробега τ и подвижностью носителей заряда µ = e/m*τ. Подвижность носителя заряда µ численно равна скорости дрейфа vдр в электрическом поле еди-
ничной напряженности ε.
Для решения задач этой темы студенты могут воспользоваться программами MCAD (см. список прил. П6, П7 и П8).
Задача 5.1. Рассчитать удельное сопротивление и теплопроводность алюминия в диапазоне температур T = 77 ... 400 К, если измеренное удельное сопротивление образца при Т = 0 ° С составляет
2,45 мкОм·см и концентрация электронов n0 = 1029 м–3 .
Для Al (см. Прил.1) находим a = 4,05 Ǻ, TD = 394 K, Tпл = 933 K.
Процессы рассеяния электронов в твердом теле можно подразделить на несколько видов, из которых в данной задаче будем рассматривать два:
18
рассеяние электронов на фононах (тепловых колебаниях решетки) и рассеяние электронов на дефектах структуры.
Рассеяние электронов на фононах по-разному зависит от температуры. Общее выражение для электропроводности, справедливое во всем температурном диапазоне, дается следующими соотношениями Бло-
ха‒Грюнайзена:
σ |
ρ |
|
|
T |
5 |
|
|
T |
||||
(T )−1 = |
(T ) |
= 4R × |
|
|
J |
|
|
D |
, |
|||
|
|
|
||||||||||
|
|
|
п |
T |
|
|
5 |
T |
||||
|
|
|
|
D |
|
|
|
|
|
|
||
|
x |
|
|
z5 dz |
|
|
|
|
|
|
||
J5 (x) = ∫ |
|
|
|
|
|
|
|
|
, |
|
||
|
|
|
|
|
|
|
|
|
||||
|
0 |
|
(ez - 1)(1- e−z ) |
|||||||||
где Rп – приведенное идеальное сопротивление; z = hω/2πkT; x = TD /T.
Приведенные соотношения позволяют определить электропроводность металла в двух предельных случаях: T >> TD и T << TD (TD – температура Дебая), используемых на практике для расчета.
При высоких температурах T >> TD процесс рассеяния носит упругий характер, и средняя длина свободного пробега λ(T) определяется простой приближенной формулой:
λ(T ) = 50 |
Tпл |
a , |
(5.2) |
|
|||
|
T |
|
|
где: Tпл – температура плавления; a – параметр решетки материала.
характер рассеяния становится неупругим и λ(T) имеет
вид:
λ |
λ |
T 5 |
|
||
(T ) = |
(T |
)× |
D |
. |
(5.3) |
|
|||||
|
D |
T |
|
||
|
|
|
|||
Соотношения (5.2), (5.3) позволяют приближенно оценить длину свободного пробега, определяемую рассеянием электронов на тепловых колебаниях решетки (фононах). На рис. 5.1 представлены графики зависимости λ1(T) и λ2(T), рассчитанные по формулам (5.2) и (5.3) соответственно для Al.
Штрихами (×) выделен график результирующей зависимости λ(T).
Время свободного пробега электронов в чистом металле τ |
(T): |
|||||||||
|
|
|
|
3 |
|
2 |
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
3π |
n |
|
|
|
τ |
(T ) |
|
F= |
( |
|
0 |
|
|
||
f (T ) = |
, |
|
|
2π m" |
|
, |
(5.4) |
|||
|
|
|
|
|
||||||
|
vF |
|
|
|
|
|
|
|
|
|
скорость Ферми; h – постоянная Планка.
Время релаксации при рассеянии электронов на дефектах структуры в металле τd не зависит от температуры.
19
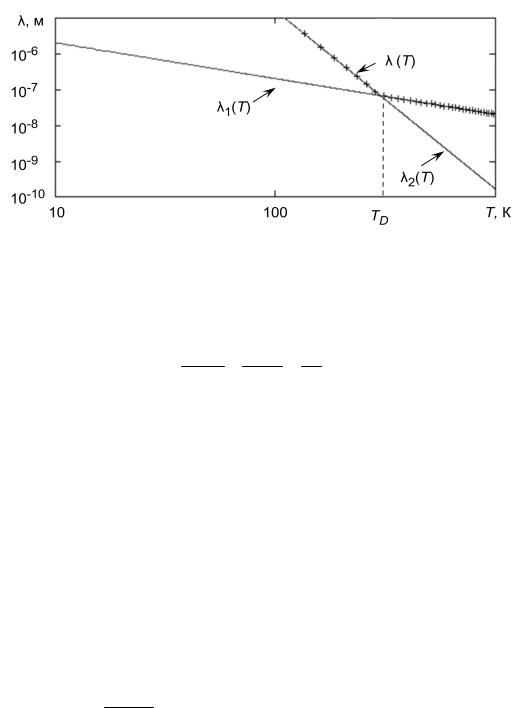
Рис. 5.1
Результирующее время релаксации τΣ при учете обоих механизмов
рассеяния определяется правилом Маттиссена: |
|
||||||
1 |
1 |
1 |
|
|
|||
|
τΣ |
= |
τ |
+ |
τ |
. |
(5.5) |
|
f (T ) |
|
|||||
|
(T ) |
|
|
d |
|
||
Формула 5.5 представляет собой алгебраическую сумму при условии преобладания одного из механизмов рассеяния.
Чтобы оценить вклад в электропроводность, вносимый рассеянием на дефектах структуры, сравним время свободного пробега электронов в чистом металле и в условиях задачи при 273 К с результирующим временем релаксации τΣ(273). Из рис. 5.1 находим λ(273) = 10–7 м, а согласно (5.4) по-
лучаем для скорости Ферми vF = 2,1·106 м/c и времени свободного пробега электронов в чистом металле τf(273) = 5·10–14 с. Используя выражение
(5.1), по заданному измеренному значению удельного сопротивления образца, равному ρ = 2,45 мкОм·см при Т = 0 ° С, находим результирующее
время релаксации τΣ(273) с учетом обоих механизмов рассеяния: |
|||||
τΣ= |
m" |
9,1×10−31 |
» 10−15 c. |
||
e2 n |
ρ= |
||||
(1,6 ×10−19 )210292,45 ×10−8 |
|||||
|
0 |
|
|
||
Сравнение показывает, что преобладает процесс рассеяния на дефектах структуры, т. к. он имеет на порядок меньшее значение (10‒15 < 10–14).
Теплопроводность κ(T) металла может быть определена на основе закона Видемана–Франца, который справедлив при высоких температурах (T >> TD), а также при температурах столь низких, что рассеяние стацио-
нарными дефектами становится преобладающим:
20
