Sb96727

Выбирается первый способ квантования и для заданных преподавателем значений диапазона генератора tm, частоты квантующих импульсов f0, числа

многократных измерений N. Затем выполняются многократные измерения, и результаты экспериментального определения числовых характеристик погрешности квантования заносятся в табл. 5.3.

В эту же таблицу заносятся результаты расчета этих же характеристик по формулам, приведенным в табл. 5.1.

Повторить вышеуказанные действия для остальных трех способов квантования по уровню.

Отчет должен содержать:

1.Гистограмму и статистическую функцию распределения для одного из способов квантования (по заданию преподавателя).

2.Выводы о соответствии результатов экспериментального и расчетного определения характеристик погрешности квантования.

Лабораторная работа 6. ОПРЕДЕЛЕНИЕ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК ЦИФРОВОГО ПЕРИОДОМЕРА

Цель работы – определение метрологических характеристик цифрового периодомера экспериментальным путем.

6.1.Задание на работу

1.Ознакомиться с назначением объектов виртуальной лабораторной работы, изображенными на экране и органами управления ими.

2.Определить шаг квантования по уровню.

3.Определить характеристики основной погрешности периодомера:

абсолютную cистематическую погрешность;

СКО случайной погрешности;

предельные значения абсолютной и относительной погрешностей.

4. Исследовать влияние параметров периодомера на погрешность измерения.

22

5.Определить расчетным и экспериментальным путем характеристики погрешности измерения частоты для различных диапазонов измерения при косвенных измерениях периодомером.

6.Сравнить результаты расчетного и экспериментального определения характеристик погрешности измерения при применении периодомера.

6.2. Методические указания к работе

Общие сведения. Результат преобразования периодомера равен числу импульсов известного периода Т0, подсчитанных за период Тx. Уровни кван-

тования задаются импульсами стабильной частоты f0, шаг квантования по уровню равен периоду импульсов стабильной частоты q = Т0 = 1/f0.Число импульсов, зафиксированное СИ за период Тx равно

Nх = Тx / Т0 = Тx f0,

где f0 = 1/Т0 – частота импульсов стабильной частоты. Составляющие погрешности периодомера:

погрешность квантования;

инструментальная погрешность, обусловленная нестабильностью ГИСЧ, относительное значение которой равно г = ( f0 / f0)100%.

При построении ГИСЧ используются кварцевые резонаторы для которых погрешность нестабильности пренебрежимо мала.

Определение шага квантования. Ознакомиться с назначением объектов на экране. Далее при выполнении работы следовать инструкциям, приведенным на экране. Измеряемая величина формируется генератором в виде случайной величины равномерно распределенной в диапазоне [0; Тm].

Определить шаг квантования q = 1/f0 для периодомера с помощью расчета и эксперимента для всех возможных сочетаний значений частоты ГИСЧ f0 и всех диапазонов Тm в режиме однократных измерений. Шаг квантования q экспериментально определяется как минимальное изменение показаний, расчетное значение q = 1/f0. Занести значения шага квантования в табл. 6.1.

23

Однократные измерения. Выполнить измерения периода в режиме однократно для заданных преподавателем: предела измерения периода Тm, значения частоты ГИСЧ периодомера f0; числа измерений N.

Результаты измерения Txi и экспериментального определения абсолютной погрешности Ti записать в табл. 6.2.

Для каждого измерения определить относительную погрешность измерения периода i = ( Ti / Txi) 100 %, результаты измерения периода Txi Txi и занести их в табл. 6.2. Определить оценки предельной абсолютной 1/f0 и относительной погрешностей = (1/f0Tx) 100 % расчетным путем, результаты расчета занести в табл. 6.2.

Многократные измерения периодомером. Выполнить многократные измерения периода для значений, заданных преподавателем: предела измере-

ния генератора Тm; значения частоты f0; числа измерений N. Результаты экс-

периментального определения характеристик погрешности измерения периодомером: пределы абсолютной погрешности Tmin, Tmax, оценки математического ожидания Tср и оценки СКО σэ погрешности занести в табл. 6.3.

Определить расчетом характеристики погрешности измерения: оценки пределов абсолютной погрешности T = ± T0 и СКО р = T0/ 6 погрешности, результаты занести в табл. 6.3.

Косвенные измерения частоты периодомером. Периодомер можно применить для косвенного измерения частоты, при этом по показаниям Tx периодомера вычисляется значение частоты Fх = 1/Tx. Для экспериментального определения погрешностей косвенного измерения частоты выполнить

24

однократные измерения для заданных преподавателем значений: числа измерений N; предела измерения Тm; частоты f0. Результаты измерения периода

Тхi и погрешности Ti занести в табл. 6.4.

По полученным экспериментальным значениям рассчитать и занести в табл. 6.4 значения:

1)измеренное значение частоты Fxi = 1/Txi;

2)пределы погрешностей косвенного измерения частоты: относительной

венных измерений частоты. Занести полученные значения в табл. 6.4. Сравнить экспериментальные и расчетные значения.

Отчет должен содержать:

1.Выводы о соответствии расчетных и экспериментальных значений шага квантования периодомера расчетным значениям.

2.Выводы о соответствии расчетных и экспериментальных значений характеристик погрешности периодомера.

Лабораторная работа 7. ОПРЕДЕЛЕНИЕ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК ЦИФРОВОГО ЧАСТОТОМЕРА

Цель работы – определение метрологических характеристик цифрового частотомера экспериментальным путем.

7.1.Задание на работу

1.Ознакомиться с назначением объектов виртуальной лабораторной работы, изображенными на экране, и органами управления ими.

2.Определить шаг квантования частотомера.

3.Экспериментально определить характеристики основной погрешности частотомера:

абсолютную cистематическую погрешность;

25

СКО случайной погрешности;

пределы абсолютной и относительной погрешностей.

4.Исследовать влияние параметров частотомера на погрешность изме-

рения.

5.Определить расчетным и экспериментальным путем характеристики погрешности измерения частоты для различных диапазонов при прямых измерениях частотомером средних значений.

6.Сравнить результаты расчетного и экспериментального определения характеристик погрешности измерения при применении частотомера.

7.2. Методические указания к работе

Общие сведения. Принцип построения частотомера сходен с принципом построения хронометра. Отличие в том, что фиксирован интервал времени, за который подсчитываются импульсы измеряемой частоты. Если измеряется частота Fх импульсной последовательности, то результат преобразования Nх определяется подсчетом числа импульсов за фиксированное время tи. Число импульсов при этом равно

Nх = Fх tи,

а шаг квантования по уровню

q = Fх/Nх = 1/tи.

Погрешность частотомера складывается из погрешности квантования и инструментальной погрешности. Инструментальная погрешность обусловлена нестабильностью ГИЗД. При использовании для построения ГИЗД кварцевого резонатора погрешностью от неточного формирования интервала времени tи можно пренебречь и тогда погрешность измерения частоты сводится к погрешности квантования. Данный частотомер целесообразно применять при измерении высоких частот.

Определение шага квантования. Ознакомиться с назначением объектов на экране. Далее при выполнении работы следовать инструкциям, приведенным на экране.

Измеряемая величина формируется генератором в виде случайной величины равномерно распределенной в диапазоне [0; Fm]. Определить шаг квантования для частотомера для всех возможных сочетаний времени tи и всех диапазонов в режиме однократных измерений. Шаг квантования q определя-

26

ется как минимальное изменение показаний. Занести это значение шага квантования в табл. 7.1.

Расчетное значение шага квантования q = 1/tи. Сделать выводы об экспериментальных и расчетных значениях q.

Однократные измерения частотомером. Выполнить однократные из-

мерения частоты для заданных преподавателем: предела измерения частоты генератора Fх; значения времени измерения частотомера tи; числа измерений N. Результаты измерения частоты Fxi ± Fi, экспериментального определения

абсолютной Fi и относительной погрешностей i = ( Fi / Fxi) 100 % записать в табл. 7.2.Определить оценки пределов абсолютной 1/ tи и относительной погрешностей = (1/tи Fxi) 100 % расчетным путем, результаты расчета занести в табл. 7.2.

Многократные измерения частотомером. Выполнить измерения ча-

стоты в режиме многократно для заданных преподавателем: предела измерения частоты генератора Fm; значения времени измерения частотомера tи. Результаты экспериментального определения характеристик погрешности измерения: границы пределов погрешности Fmin, Fmax; среднее значение погрешности Fср; оценку СКО погрешности σэ занести в табл. 7.3.

27

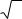
Определить расчетом характеристики погрешности измерения: пределы абсолютной погрешности F = ± 1/tи; СКО погрешности р = 1/(tи 6 ) и за-

нести их значения в табл. 7.3.

Отчет должен содержать:

1.Выводы о соответствии расчетных и экспериментальных значений шага квантования частотомера.

2.Выводы о соответствии расчетных и экспериментальных значений характеристик погрешности частотомера.

II. ВАРИАНТЫ ЗАДАЧ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ

II.1. Принцип аналого-цифрового преобразования. Коды, применяемые в ЦИУ

1.Чему равна частота дискретизации при ступенчатой экстраполяции синусоидального сигнала частоты 100 Гц, если приведенная погрешность восстановления сигнала не превышает 1 %?

2.Чему равна приведенная погрешность восстановления сигнала по его отсчетам для ступенчатой экстраполяции при преобразовании синусоидального сигнала частоты 50 Гц, если частота дискретизации 100 кГц?

3.Сколько двоичных разрядов достаточно для представления числа 567 двоичным кодом?

4.Чему равна приведенная погрешность восстановления сигнала по дискретным отсчетам для линейной интерполяции при преобразовании синусоидального сигнала частоты 50 Гц, если шаг дискретизации 10 мкс?

5.Чему равна частота дискретизации при линейной интерполяции синусоидального сигнала частоты 1 кГц, если приведенная погрешность восстановления сигнала не превышает 0,2 %?

6.Чему равна частота дискретизации при ступенчатой экстраполяции соидального сигнала частоты 1 кГц, если приведенная погрешность восстановления сигнала не превышает 0,2 %?

7.Чему равна частота дискретизации при линейной интерполяции синусоидального сигнала частоты 1 кГц, если приведенная погрешность восстановления сигнала не превышает 0,2 %?

8.Какое максимальное значение можно представить 12-разрядным двоичным кодом?

9.Какое максимальное число можно представить 4-разрядным двоичнодесятичным кодом?

28

II.2. Метрологические характеристики для представления результатов измерений

1.Число двоичных разрядов АЦП 10, предел измерения 10,24 В. Чему равен шаг квантования?

2.Предел измерения 8-и разрядного АЦП 2,56 В, значение выходного кода 209.Чему равен результат преобразования?

3.Предел измерения 10-разрядного АЦП 10,24 В, значение выходного кода 756. Чему равен результат преобразования?

4.Предел измерения 9-и разрядного АЦП 5,12 В, значение выходного кода 437. Чему равен результат преобразования?

5.Чему равна единица младшего разряда 4-разрядного вольтметра на пределе100 В?

6.Число разрядов частотомера 6, предел измерения 1 МГц. Чему равен шаг квантования?

7.Чему равен уровень компарирования идеальной статической характеристики 4-разрядного вольтметра, если его показания 7,98 В, а предел измерения 10 В?

8.Чему равны единицы младшего разряда 8-разрядного частотомера на каждом из пределов измерения: 1 кГц; 10 кГц; 100 кГц?

9.Определите число разрядов отсчетного устройства цифрового частотомера, если предел измерения 1 кГц, а единица младшего разряда 0,1 Гц.

II.3. Метрологические характеристики для оценки основной погрешности

1.Чему равно минимальное число разрядов АЦП, чтобы приведенная погрешность квантования не превышала 0,1 %?

2.Сколько двоичных разрядов должен иметь выходной код АЦП, чтобы приведенная погрешность квантования не превышала 0,5 %?

3.Класс точности цифрового омметра 0,5/0,2, предел измерения 100 кОм. Чему равны относительная и абсолютная погрешности измерения, если показания омметра 58,58 кОм?

4.Класс точности цифрового вольтметра 0,2/0,1, предел измерения 10 В, показания вольтметра 8,675 В. Чему равны относительная и абсолютная погрешности измерения?

5.Класс точности частотомера 0,01/0,005, предел измерения 10 кГц. Чему равны относительная и абсолютная погрешности измерения, если показания равны 6,55 кГц?

29

6.Чему равна приведенная погрешность квантования 4-разрядного вольтметра?

7.Чему равно СКО погрешности квантования для 10-разрядного АЦП, если его предел измерения 10,24 В?

8.Чему равно СКО погрешности квантования для 4-разрядного вольтметра если его предел измерения 10 В?

9.Чему равна приведенная погрешность квантования 12-разрядного АЦП, если способ квантования отождествление с ближайшим или равным уровнем?

II.4. Динамические метрологические характеристики

иоценка динамической погрешности

1.Чему равна приведенная динамическая погрешность 2 рода при преобразовании синусоидального сигнала частоты 50 Гц, если максимальная ча-

стота преобразования АЦП 106 пр/сек?

2.Чему равна максимальная частота преобразования АЦП при преобразовании синусоидального сигнала частоты 100 Гц с приведенной динамическая погрешностью не более 0,2 %?

3.Динамический диапазон сигнала 10 В, максимальная частота спектра 1кГц. Чему равна приведенная динамическая погрешность 2 рода, если мак-

симальная частота преобразования АЦП 108 пр/сек?

4.Чему равна максимальная частота преобразования АЦП при преобразовании сигнала с динамическим диапазоном 5 В и максимальной частотой спектра 3000 Гц c приведенной динамической погрешностью не более 0,5 %?

5.Чему равна приведенная динамическая погрешность при преобразовании синусоидального сигнала частоты 1кГц, если апертурное время УВХ

10 нс?

6.Во сколько раз уменьшается приведенная динамическая погрешность при применении УВХ, если время преобразования АЦП 1 мкс, а апертурное время УВХ 10 нс?

7.Во сколько раз увеличивается частотный диапазон при применении УВХ, если время преобразования АЦП 1мкс, а апертурное время УВХ 20 нс?

8.Чему равно апертурное время УВХ при уменьшении приведенной ди-

намической погрешности 2 рода в 10 раз, если быстродействие АЦП 106 пр/сек?

9. Быстродействие АЦП 107 пр/сек. Определите апертурное время УВХ

для уменьшения приведенной динамической погрешности 2 рода в 20 раз.

30