
Sb97281
.pdf
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)
А. Ю. ПЕЧЕНКОВ С. А. ГАЛУНИН
РЕШЕНИЕ ЗАДАЧ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
И МАГНИТНОГО ПОЛЯ ПОСТОЯННОГО ТОКА
Учебно-методическое пособие
Санкт-Петербург Издательство СПбГЭТУ «ЛЭТИ»
2018
УДК 621.365.5
ББК 31.2
П31
Печенков А. Ю., Галунин С. А.
П31 Решение задач электростатического поля и магнитного поля постоянного тока: учеб.-метод. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ»,
2018. 24 с.
ISBN 978-5-7629-2282-1
Содержит решения типовых задач электростатического поля и магнитного поля постоянного тока.
Предназначено для подготовки магистров по направлению 13.04.02 «Электроэнергетика и электротехника» по программе «Электротехнологии», а также может быть полезно студентам других специальностей.
УДК 621.365.5
ББК 31.2
Рецензент канд. техн. наук В. С. Федорова (ПГУПС Императора Александра I).
Утверждено
редакционно-издательским советом университета
в качестве учебно-методического пособия
ISBN 978-5-7629-2282-1 |
© СПбГЭТУ «ЛЭТИ», 2018 |
|
1. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ |
|
|
||||
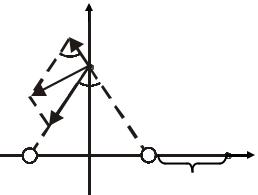
Задача 1.1. Два точечных заряда рассматриваются в декартовой системе |
|||||||
координат (рис. 1.1). Первый заряд расположен в точке с координатами (2; 0; |
|||||||
0) и равен Q = 10 11 Кл. Второй заряд расположен в точке с координатами |
|||||||
|
1 |
|
|
|
|
|
|
( 2; 0; 0) |
и равен Q = 4 |
|
10 11 Кл. |
|
y |
|
|
|
2 |
|
|
|
|
|
|
Координаты точек даны в сантиметрах. |
E1 |
3 см |
|
||||
|
|
|
|
|
|||
Относительная диэлектрическая про- |
2 |
|
|||||
|
|
|
|||||
ницаемость среды равна r = 1. |
|
|
|
||||
E |
|
r1 |
|
||||
1. Вычислите значение и укажите |
1 |
|
|||||
|
|
|
|||||
направление напряженности |
электри- |
E2 |
r2 |
Q1 |
|
||
|
|
||||||
ческого поля в точке (0; 3; 0). |
|
|
|
|
x |
||
2. Найдите координаты |
точки с |
Q2 |
|
l |
|||
|
|
||||||
нулевой |
напряженностью |
электриче- |
2 см |
|
2 см |
|
|
|
|
|
|
||||
ского поля. Сколько имеется таких то- |
|
Рис. 1.1 |
|
|
|||
|
|
|
|
|
|
|
|
чек? |
|
|
|
|
|
|
|
Решение:
1. Чтобы найти напряженность поля в требуемой точке, необходимо определить сначала компоненты напряженности электрического поля в этой точке.
Составляющие E1 и E2 вектора напряженности электрического поля E в требуемой точке действуют по прямым, соединяющим исследуемую точку с зарядами Q1 и Q2. Направление векторов E1 и E2 выбирается исходя из того, что в исследуемой точке находится единичный положительный заряд.
Чтобы найти E1 и E2, надо сначала найти расстояния r1 и r2. Поскольку треугольник 2 см; +3 см; +2 см равнобедренный, то r1 = r2. Тогда из прямоугольного треугольника 0 см; +3 см; +2 см находим, что
r12 r22 2 10 2 2 310 2 2 1310 4 м.
Значения составляющих напряженности электрического поля в исследуемой точке:
E1 |
|
|
Q1 |
|
|
|
|
1 10 11 |
|
|
69,2 В/м; |
||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||
4r 2 |
|
|
|
4 1310 |
4 |
8,85 |
10 12 |
|
|||||
|
|
0 |
r |
|
1 |
||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|||
3
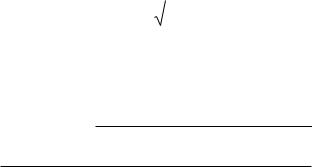
E2 |
|
|
Q2 |
|
|
|
|
|
4 10 11 |
|
|
276,8 В/м . |
||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
4r 2 |
|
|
|
|
4 1310 |
4 |
8,85 |
10 12 |
|
|||||
|
|
0 |
r |
|
1 |
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
||||
В векторной форме имеем: E1 = 69,2 В/м; E2 = 276,8 В/м. Результирующая напряженность электрического поля находится из ре-
шения треугольника с углом 2 напротив гипотенузы E. Углы 2 и 1 равны: 2 = 1 = . Для нахождения угла найдем сначала косинус его половины:
|
|
|
310 |
2 |
|||
cos |
|
|
|
|
|
|
0,832. |
|
|
|
|
|
|||
|
2 |
|
1310 4 |
||||
Отсюда получаем, что = 2 arccos (0,832) = 2 33,7 = 67,4 . С помо-
щью теоремы косинусов находим модуль результирующей напряженности электрического поля в исследуемой точке:
E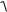
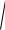 E12 E22 2 E1 E2 cos
E12 E22 2 E1 E2 cos

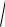 69,22 276,82 2 69,2 276,8 cos67,4 258,3 В/м .
69,22 276,82 2 69,2 276,8 cos67,4 258,3 В/м .
2. Точка, в которой напряженность электрического поля равна нулю, может находиться только на прямой, соединяющей заряды, причем правее заряда Q1. Обозначим это расстояние через l.
Учитывая, что заряд Q2 по абсолютному значению в 4 раза больше заряда Q1, можем записать:
4 |
Q1 |
|
|
|
|
Q1 |
|
. |
|||
|
|
|
|
|
|
|
|||||
|
4 0,04 l 2 0 r |
4 l |
2 |
0 r |
|||||||
После сокращений имеем: |
|
|
|
|
|
|
|
||||
4 |
|
1 |
. |
||||||||
|
|
0,04 l 2 |
|
||||||||
|
|
|
|
l 2 |
|||||||
Решив полученное квадратное уравнение, находим, что l = 0,04 м. Следовательно, координата x = 0,02 + 0,04 = 0,06 м, а координаты найденной точки (6; 0; 0).
Задача 1.2. Следующая векторная функция дает возможное электростатическое поле: Ex = 6xy; Ey = 3x2 – 3y2; Ez = 0. Вычислите линейный интеграл от E от точки (0, 0, 0) до точки (x1, y1, 0) вдоль пути, который идет прямо от
4

точки (0, 0, 0) до точки (x1, 0, 0) и оттуда в точку (x1, y1, 0) (рис. 1.2). Вычислите такой же путь, который идет вдоль двух других сторон четырехугольни-
ка через точку (0, y1, 0). Сделайте вывод о право-
y
мерности описания электростатического поля за- |
|
|
|
данной векторной функцией. Определите градиент |
y1 |
|
|
найденной функции (x, y, z) и посмотрите, получи- |
|
|
|
ли ли вы таким образом компоненты заданного по- |
|
x |
|
0 |
x1 |
||
ля. |
|||
|
|
Решение. Линейный интеграл от E от точки |
Рис. 1.2 |
|
|
(0, 0, 0) до (x1, y1, 0) вдоль пути, который идет от |
|
точки (0, 0, 0) до (x1, 0, 0) и оттуда в точку (x1, y1, 0), находится следующим образом:
x1 |
, y1, 0 |
x1 |
, 0, 0 |
x1 |
, y1, 0 |
|
Edl |
|
Edl |
|
Edl |
0, 0, 0 |
0, 0, 0 |
x1, 0, 0 |
|||
|
x , 0, 0 |
x , y , 0 |
3x2 3y2 |
dy |
|
|
x x1 |
3x2 y y3 |
|||
|
6x2 y |
y 0 |
|||||||||
|
1 6xydx |
1 1 |
|||||||||
2 |
|
x 0 |
|||||||||
|
0, 0, 0 |
x1, 0, 0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
y 0 |
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
0 3x2 y y3 |
3x2 y y3. |
||||||||
|
|
|
1 |
1 |
1 |
|
1 |
1 |
1 |
||
x x1
y y1 x x1
y 0
Линейный интеграл от E по пути, который идет вдоль двух других сторон четырехугольника через точку (0, y1, 0) находится аналогично найденному ранее:
x1 |
, y1, 0 |
0, y1, 0 |
x1 |
, y1, 0 |
|
Edl |
Edl |
|
Edl |
0, 0, 0 |
0, 0, 0 |
0, y1, 0 |
||
|
0, y1, 0 |
3x2 |
x1, y1, 0 |
|
|
|
|
3y2 dy |
6xydx 3x |
||
|
0, 0, 0 |
|
0, y1, 0 |
|
|
|
|
|
0 y3 |
3x2 y 0 |
|
|
|
|
1 |
1 |
1 |
x 0
2 y y3 y y1 x 0 y 0
3x12 y1 y13.
|
|
|
x x1 |
|
|
|
6x2 y |
|
y y1 |
|
|
2 |
x 0 |
||||
|
|
||||
|
|
|
y y1 |
|
|
Так как в обоих случаях получен одинаковый результат, то предложенная векторная функция может описывать электростатическое поле.
5
Градиент найденной функции: |
3x2 y |
y3 |
|
|
3x2 y |
y3 |
|
|
|
||||||||
grad i |
|
j |
|
k |
i |
1 1 |
1 |
|
|
j |
1 |
1 |
1 |
|
|
0 |
|
x |
y |
x |
|
|
|
|
y |
|
|
|
|||||||
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
(6x y )i (3x2 3y2 ) j. |
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
Компоненты заданного поля получены: Ex = 6xy; Ey = 3x2 – 3y2; Ez = 0. Задача 1.3. Вычислите компоненты вектора E и покажите, что век-
торная функция, определенная в задаче 1.2, является возможным электростатическим полем (решив предыдущую задачу, вы доказали это другим способом, определив скалярную функцию, градиентом которой является поле). Вычислите дивергенцию поля.
Решение. Если rot E = 0, то векторная функция E является возможным
электростатическим полем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iEx jE y kEz |
|
|
|
|
||||||||||
E i |
|
|
j |
|
|
|
k |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
x |
|
y |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
E |
z |
E y |
|
|
|
|
E |
x |
|
|
E |
z |
|
|
|
E y |
|
E |
x |
|
|
|
|
|||||||||||
i |
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
y |
|
z |
|
|
|
|
|
|
z |
|
|
|
x |
|
|
x |
|
y |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
i 0 0 j 0 0 k 6x 6x 0; |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
E |
x |
|
|
E y |
|
|
E |
z |
|
|
|
|
(6xy) |
|
(3x2 3y2 ) |
|
(0) |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x |
|
|
y |
|
|
z |
|
|
|
|
x |
|
|
|
y |
|
|
|
z |
|||||||||||||||
div E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 y 6 y 0 0.
Задача 1.4. 1. Удовлетворяет ли функция f(x, y) = x2 + y2 двумерному уравнению Лапласа? А функция g(x, y) = x2 y2? 2. Постройте график последней функции. 3. Вычислите градиенты функции g(x, y) в точках с координатами (0, 1); (1, 0); (0, 1); ( 1, 0) и укажите направления векторов этих градиентов.
Решение:
1. Уравнение Лапласа имеет вид 2 0 , где оператор 2 div grad называют оператором Лапласа или лапласианом. Иногда его обозначают символом . Поэтому можно встретить и такую форму записи уравнения Лапласа: 0 . Таким образом, если вторая производная по координатам от предложенной функции равна нулю, то функция удовлетворяют уравнению Лапласа. Имеем:
6

|
|
2 f |
2 |
x2 y2 |
|
|
2 x2 y2 |
2 2 4 0; |
|||||||||
|
|
|
|
x2 |
|
|
|
y2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 g |
2 x2 y2 |
|
2 x2 y2 |
|
2 |
2 |
0. |
||||||||
|
|
|
x2 |
|
y2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. График функции g(x, y) = x2 y2 пока- |
|
|
|
|
|
||||||||||||
зан на рис. 1.3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Градиент функции g(x, y): |
|
|
|
|
|
|
|
|
|||||||||
g |
x2 y2 |
i |
x2 |
y2 |
|
j 2xi 2 yj . |
|
|
|
|
|
||||||
x |
|
|
|
y |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Градиент |
функции |
g(x, y) |
в точке |
|
|
|
|
|
|||||||||
(x = 0, y = 1): |
g 2 j . |
Вектор направлен |
|
|
|
|
Рис. 1.3 |
||||||||||
вдоль отрицательного направления оси ординат. Градиент функции g(x, y) в точке (x = 1, y = 0):
лен вдоль положительного направления оси абсцисс.
Градиент функции g(x, y) в точке (x = 0, y = 1): g 2 j . Вектор направлен вдоль положительного направления оси ординат.
Градиент функции g(x, y) в точке (x = 1, y = |
0): g 2i . Вектор на- |
||||||||||||||||
правлен вдоль отрицательного направления оси абсцисс. |
|
|
|
|
|
|
|
|
|||||||||
Задача 1.5. 1. Начертите «силовые линии» |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
y |
|
|
|
|
|
|||||||
для векторной функции A = jx + iy в плоско- |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
сти xy. 2. Вычислите rot A и укажите направле- |
|
|
|
|
|
|
|
|
|
|
|
||||||
ние этого вектора. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. «Силовые линии» для векторной функ- |
|
|
|
|
|
|
|
|
|
|
|
||||||
ции A = jx + iy в плоскости xy |
показаны на |
|
|
|
|
|
|
|
|
|
|
|
|||||
рис. 1.4. |
|
|
|
|
|
|
|
|
|
|
Рис. 1.4 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
2. Ротор функции A: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
Ay |
|
A |
A |
|
|
Ay |
|
A |
|
|
|
|
|||
rot A i |
z |
|
j |
x |
z |
k |
|
|
|
|
x |
|
|||||
|
|
|
|
||||||||||||||
|
y |
|
|
|
z |
x |
|
|
x |
|
y |
|
|
|
|
||
|
z |
|
|
|
|
|
|
|
|||||||||
i 0 0 j 0 0 k 1 1 2k.
Вектор rot A = 2k направлен по отрицательному направлению оси z.
7

Задача 1.6. Вычислите ротор и дивергенцию каждого из следующих векторных полей. Если ротор окажется равным нулю, то определите скалярную функцию , градиент которой дает векторное поле:
1.Fx = x + y, Fy = x + y, Fz = 2z.
2.Gx = 2y, Gy = 2x + 3z, Gz = 3y.
3.Hx = x2 z2, Hy = 2, Hz = 2xz.
Решение:
1.Имеем векторную функцию F = i(x + y) + j(x + y) + k( 2z):
|
F |
Fy |
|
F |
F |
Fy |
|
F |
|
|
||
rot F i |
z |
|
|
j |
x |
z |
k |
|
|
x |
|
|
|
|
|||||||||||
|
y |
z |
|
|
z |
x |
|
x |
|
y |
|
|
|
|
|
|
|
|
|||||||
i 0 0 j 0 0 k 1 1 2k;
|
|
|
|
F |
|
|
|
Fy |
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
div F |
|
x |
|
|
|
|
|
|
z |
1 1 2 0. |
|
|
|
|
|
|||||||||||
|
|
y |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|||||
2. Имеем векторную функцию G = i(2y) + j(2x + 3z) + k(3y): |
|
|
|||||||||||||||||||||||||
|
G |
|
Gy |
|
|
|
|
G |
x |
G |
|
|
Gy |
|
G |
x |
|
|
|||||||||
rot G i |
|
z |
|
|
|
|
|
j |
|
|
|
|
|
|
z |
k |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
y |
|
z |
|
|
|
|
|
|
|
z |
|
|
x |
|
x |
|
y |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
i 3 3 j 0 0 k 2 2 0; |
|
|
|
|
|
||||||||||||||||||||
div G |
G |
x |
|
Gy |
|
|
|
G |
z |
0 0 0 0; |
|
|
|
|
|||||||||||||
|
|
|
y |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|||||
Gi(2 y) j(2x 3z) k(3y) grad i x j y k z ;
2 yx 3zy.
3. Имеем векторную функцию H = i(x2 z2) + j(2) + k(2xz):
|
H |
|
|
H y |
|
H |
|
|
H |
|
H y |
|
H |
|
|
|
||||||
rot H i |
|
z |
|
|
|
|
j |
|
|
x |
|
z |
k |
|
|
|
x |
|
||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
y |
|
z |
|
|
|
z |
|
|
x |
|
|
y |
|
|
|||||||
|
|
|
|
|
|
x |
|
|
|
|||||||||||||
|
i 0 0 j 2z 2z k 0 0 4zj; |
|
|
|
|
|
||||||||||||||||
div H |
H |
x |
|
H y |
|
H |
z |
2x 0 2x 4x. |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
y |
|
z |
|
|
|
||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
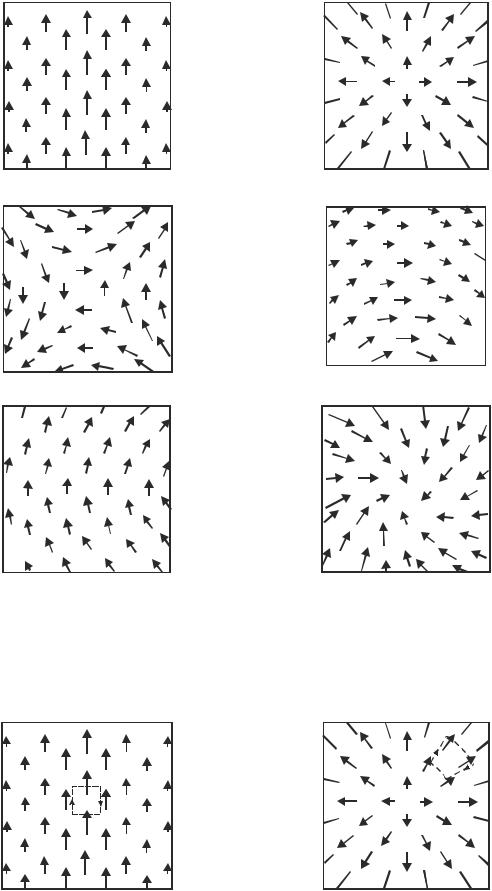
Задача 1.7. Укажите, в каких двумерных полях вектора F: 1) rot F = 0, а
в каких rot F 0; 2) div F = 0, а в каких div F 0.
8
|
|
|
|
|
а |
б |
|
в |
г |
д |
е |
Рис. 1.5
Решение:
1. Заметьте (рис. 1.5, а), что вектор остается постоянным, если продвигаться в его направлении, т. е. F/y = 0, Fx = 0. Следовательно, div F = 0.
|
|
|
|
|
а |
б |
|
9
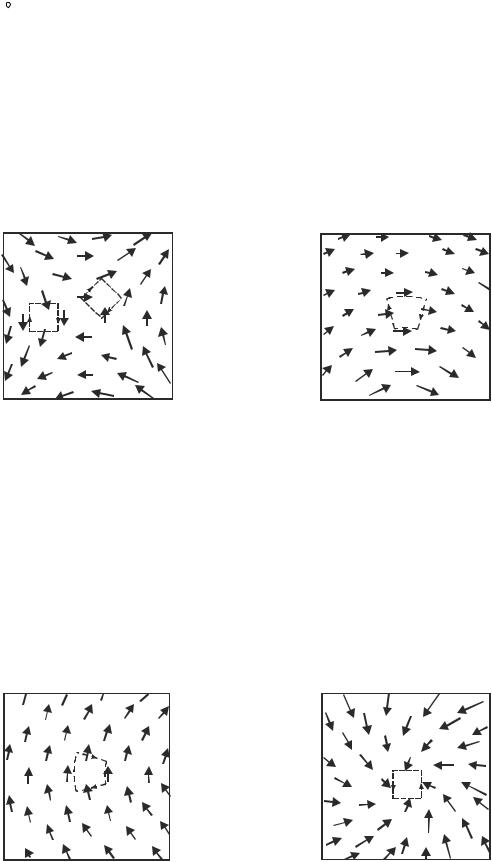
Обратите внимание на то, что линейный интеграл вдоль изображенного контура Fdl не равен нулю. Следовательно, rot F 0.
l
2. Заметьте (рис. 1.5, б), что функция F радиальная. Это значит, что для данного радиуса ее значение постоянно. Поэтому циркуляция F равна нулю как вокруг изображенного, так и любого другого контура. Следовательно, rot F = 0. Очевидно, что div F 0.
3. Циркуляция F может быть равной нулю вокруг изображенных контуров, следовательно rot F = 0. Однако из одного рис. 1.5, в не очевидно, что div F = 0, но видно, что она могла бы быть равной нулю.
в |
г |
4. Если продвигаться в направлении вектора F, то нет изменений в его значении (рис. 1.5, г). Этого достаточно, чтобы div F = 0. Циркуляция F может быть равна нулю вокруг изображенного контура, если на длинной стороне контура произведение Fdl равно произведению Fdl на короткой стороне контура. Следовательно, rot F = 0.
5. Если продвигаться в направлении вектора F (рис. 1.5, д), то его значение постоянно, следовательно, div F = 0. В данном примере вектор F всюду постоянен, поэтому линейный интеграл по длинной стороне не компенсируется интегралом по короткому пути и циркуляция не равна нулю, следова-
тельно, rot F 0.
д |
е |
10
