Sb95734

МИНОБРНАУКИ РОССИИ

––––––––––––––––––––––––––––––––––––––––––––––––––––

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)

––––––––––––––––––––––––––––––––––––––––––––

Е. Б. СОЛОВЬЕВА

МЕТОДЫ СИНТЕЗА НЕЛИНЕЙНЫХ ПРЕОБРАЗОВАТЕЛЕЙ СИГНАЛОВ

Электронное учебное пособие

Санкт-Петербург Издательство СПбГЭТУ «ЛЭТИ»

2017

1

УДК 621.3.011.74 (07) ББК З 811.72я7

С60

Соловьева Е. Б.

С60 Методы синтеза нелинейных преобразователей сигналов: электрон. учеб. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2017. 48 c.

ISBN 978-5-7629-2115-2

Содержит основные сведения об операторном подходе к моделированию и синтезу нелинейных дискретных цепей, а также материал, посвященный использованию системы MATLAB для анализа линейных электрических цепей.

Предназначено для студентов всех специальностей и направлений ФКТИ, может быть полезно магистрам, аспирантам, преподавателям и научнотехническим работникам университета.

УДК 621.3.011.74 (07) ББК З 811.72я7

Рецензенты: кафедра «Электроснабжение» Ульяновского государственного технического университета; д-р техн. наук А. А. Ланнэ (СПбГУТ).

Утверждено редакционно-издательским советом университета

в качестве электронного учебного пособия

2

Моделирование и синтез преобразователей сигналов, реализуемых на базе аналоговых и дискретных цепей, существенно усложняется в условиях роста интеграции и повышения требований к качеству обработки сигналов систем различного назначения (электротехнических, радиоэлектронных, телекоммуникационных, электроакустических и т. д.) В этой связи операторный подход, когда устройство представляется в виде «черного ящика», а информация о нем содержится в операторном уравнении, описывающем однозначное соответствие между множествами входных и выходных сигналов, является безусловно перспективным, а иногда единственно возможным способом исследования нелинейных процессов в сложных аналоговых и дискретных цепях [1]–[5].

Цель учебного пособия – познакомить читателя с известными математическими формами операторных моделей нелинейных дискретных цепей (НДЦ), методами идентификации полиномиальных моделей Вольтерры во временной и частотной областях, а также методами синтеза операторов НДЦ на примерах построения демодулятора, фильтра импульсных помех, компенсатора нелинейных искажений сигналов в каналах связи (КС); помочь в выполнении курсового расчета по теории электрических цепей с использованием пакета MATLAB.

1. ОПЕРАТОРНЫЕ УРАВНЕНИЯ И ФОРМЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ НЕЛИНЕЙНЫХ ДИСКРЕТНЫХ ЦЕПЕЙ

Операторное уравнение, описывающее однозначное соответствие между множествами входных и выходных сигналов НДЦ, имеет вид

где X , Y o – множества входных и выходных сигналов цепи соответственно; Fs – нелинейный оператор цепи, определяющий нелинейное математическое

преобразование.

Однозначность отображения множеств исключает ситуацию, когда одному входному сигналу соответствуют разные выходные сигналы цепи [1] – [5].

Уравнение (1.1) можно записать в форме следующего равенства:

3

дискретное время, Gn – длительность финитных или период периодических сигналов.

Нелинейность оператора Fs обусловлена следующими свойствами опе-

раторного уравнения (1.2) НДЦ:

– неоднородностью

Fs x(n) Fs x(n) ,

где – постоянная;

– неаддитивностью

Fs x1(n) x2(n) ... xm (n) Fs x1(n) Fs x2(n) ... Fs xm (n) ,

где x1(n) X , x2 (n) X , ..., xm (n) X .

Построение нелинейного оператора Fs по однозначному соответствию вход-выход (на основе множеств входных и выходных сигналов НДЦ) воз-

НДЦ обладает свойством непрерывности, т. е. реакции цепи на сигналы, отличные от испытательных, но принадлежащие заданному классу воздействий ( x(n) X , x(n) X ), мало отличаются от реакций на соответству-

ющие испытательные сигналы.

В результате с учетом равенства (1.3) можно утверждать, что нелинейный оператор F с погрешностью однозначно отображает множество X во

множество Y o , т. е.

4

Уравнение (1.4) означает, что оператор F аппроксимирует оператор Fs

где c вектор параметров оператора F . Согласно свойству непрерывности

НДЦ полученное решение (вектор c ) задачи (1.5) является решением более общей задачи аппроксимации

На практике норма погрешности аппроксимации оператора Fs оператором F рассматривается в равномерной метрике (C )

и в среднеквадратичной метрике ( L2 )

Математическое представление нелинейного оператора F называется математической моделью НДЦ. Существует несколько универсальных форм представления оператора F . К ним относятся:

–функциональный ряд Вольтерры [1] – [5];

–функциональный полином Вольтерры [1] – [5];

–полином расщепленных сигналов [1], [5];

–нелинейная авторегрессионная модель [6];

–нейронная цепь [1] – [3], [5], [7], [8].

На основе математического описания цепи в виде операторного уравнения (1.4) можно характеризовать процессы идентификации, моделирования и синтеза НДЦ следующим образом.

Идентификация цепи это процесс построения нелинейного оператора F (определение параметров математической модели цепи в результате решения задачи (1.5)) по известным множествам входных и выходных сигна-

5

лов. В качестве испытательных входных сигналов НДЦ могут быть использованы как детерминированные, так и случайные сигналы.

Математическое моделирование цепи это использование полученной в процессе идентификации НДЦ математической модели для расчета выходных сигналов цепи.

Синтез цепи это создание физически или программно-реализуемого объекта, выполняющего заданное функциональное назначение, например фильтрацию, детектирование, компенсацию и т. д.

Рассмотрим указанные универсальные формы моделей НДЦ, обладающих свойством стационарности. НДЦ стационарна, если ее реакция инвариантна по отношению к моменту появления входного сигнала; параметры стационарной НДЦ постоянны во времени.

1.1. Функциональный ряд и полином Вольтерры

Дискретная форма ряда Вольтерры [1] – [5] имеет вид

– функционал Вольтерры степени k . Функционал Вольтерры обладает свойством однородности

Многомерная функция hk m1,m2 ,..., mk называется ядром Вольтерры порядка k .

При k 0 функционал нулевой степени является константой h0 , опи-

сывающей ненулевые начальные условия в цепи.

При k 1 выражение (1.7) представляет собой линейную свертку, описывающую линейную подсистему с импульсной характеристикой h(n) .

6

При k 1 многомерная сумма (1.7) нелинейна относительно входного сигнала, поэтому ее называют нелинейной сверткой порядка k . Такая свертка формирует выходной сигнал нелинейной подсистемы порядка k с ядром hk m1,m2 ,..., mk , называемым многомерной импульсной характеристикой

порядка k .

Ядра Вольтерры симметризуются, т. е. полагаются равными

где сумма вычисляется по всем перестановкам аргументов m1,m2 ,...,mk .

Введение симметризации устраняет неоднозначность в определении ядер (симметризованные ядра не меняют своего значения при перестановках переменных m1, m2 ,...,mk ).

Однородные функционалы с симметризованными ядрами называются

регулярными.

Отрезок функционального ряда Вольтерры дает приближенное аналитическое представление реакции цепи через ее параметры и воздействие. Установленная зависимость универсальна в том смысле, что справедлива при любых воздействиях, лишь бы их амплитуды обеспечивали сходимость ряда Вольтерры. Условие сходимости ряда Вольтерры выполняется при малых амплитудах воздействия, когда режим работы НДЦ слабонелинейный.

В режиме существенной нелинейности, когда функциональный ряд Вольтерры расходится, соотношение вход-выход НДЦ можно описать функциональнымполиномомВольтеррыстепени L [1] – [5]

Принципиально такая возможность следует из теоремы М. Фреше [1] – [5]. Теоретический результат формулируется следующим образом: если зависимость реакции цепи от воздействия описывается непрерывным оператором, то при любом множестве воздействий, равномерно ограниченных по норме, можно найти функциональный полином Вольтерры, аппроксимирующий с заданной точностью в метрике L2 нелинейный оператор цепи на ко-

нечном интервале времени.

Отметим, что полином (1.8) и отрезок ряда Вольтерры (1.6) имеют одинаковую математическую форму записи, однако их параметры – ядра Вольтерры – различны [1] – [5].

7

1.2. Многочлен расщепленных сигналов

Согласно теории расщепления сигналов [1], [5] оператор F НДЦ представляется композицией двух операторов: оператора Fp расщепителя и опе-

ратора PL нелинейного безынерционного преобразователя (НБП). Оператор-расщепитель Fp преобразует скалярные входные сигналы

x(a,n) X НДЦ, где a Ga – вектор из множества Ga параметров воздействия, в соответствующие векторные сигналы

x p a, n Fp x a, n x p1 a, n , x p2 a, n , ..., x pm a, n t

(t – знак транспонирования) таким образом, чтобы выполнялись условия:

– векторные сигналы не исчезали, т. е. x p a,n 0 при всех x a,n X ;

– векторные сигналы в каждый момент времени разные, т. е. при любых a1 a2 , a1 Ga , a2 Ga , n1 n2 , n1 0,Gn , n2 0,Gn справедливо нера-

венство xp a1, n1 xp a2, n2 .

Из таблицы видно, что рассматриваемый сигнал в разные моменты времени ( nT / 2 и 3 / 2 ) принимает одинаковые значения (равен нулю). Следовательно, сигнал x nT не расщеплен по переменной времени n .

Расщепленным сигналом является векторный сигнал x p nT cos nT , sin nT t ,

поскольку значения сигнала x p nT , указанные в таблице, различны при раз-

ных n .

Расщепление сигналов реализуется различными (линейными, нелинейными, стационарными, нестационарными) математическими преобразовани-

8

ями [1], [5]. Способы расщепления зависят от класса расщепляемого сигнала. Важным критерием выбора способа расщепления является минимальность числа каналов расщепителя (минимальность длины вектора расщепленных сигналов).

Оператор НБП отображает векторные сигналы x p a, n в скалярные выходные сигналы y n Y цепи. Обычно такой оператор описывается много-

где L I1 I2 ... Im .

Возможны и другие формы представления оператора PL , например в виде дробно-рациональной функции, экспоненциального многочлена и др. [1], [5].

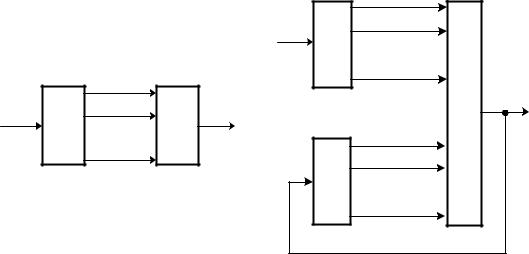
Операторному уравнению (1.9) соответствует нерекурсивная функциональная схема модели НДЦ, изображенная на рис. 1.1, а.

Наряду с нерекурсивной моделью (1.9) НДЦ возможно конструирование рекурсивной модели, описываемой уравнением

y(n) PL x p a, n

x p1 a,n i1 x p2 a,n i2 ... x pm a,n im

y p(m 1) a,n im 1 y p(m 2) a,n im 2 ... y p a,n i ,

где x p1 a, n , x p2 a, n , ..., x pm a, n , y p(m 1) a, n , y p(m 2) a, n , ...,

Im 2 ... I .

9

Функциональная схема рекурсивной модели НДЦ представлена на рис. 1.1, б. Особенность рекурсивной модели состоит в необходимости учета условий устойчивости при ее построении, что весьма сложно в случае моделирования нелинейных дискретных цепей.

1.3. NARMAX-модель

НДЦ можно описать с помощью NARMAX-модели [6] (Non-linear AutoRegressive Moving Average model with eXogenous inputs – нелинейная авто-

регрессионная модель со скользящим средним при внешних воздействиях), имеющей вид

y n F x n , x n 1 , ..., x n Nx , y n 1 , ..., y n N y ,

от входного сигнала помеха, действующая на цепь.

Значение max N x , N y , Ne определяет порядок модели (1.10).

NARMAX-модель получила свое название в силу возможности формирования на ее основе скользящего среднего и авторегрессионного процессов.

Скользящим средним называется процесс на выходе линейной нерекурсивной подсистемы порядка Nx , описываемой разностным уравнением

y n b0x n b1x n 1 ... bN x x n Nx .

10