2.3.1 Приклади розв’язання задач

2.21 На склад надходять електричні лампочки від трьох заводів. Від першого – 30 % від загальної кількості що надійшли, від другого – 25 %, від третього – 45 %. На першому заводі брак складає 1 % від загальної продукції, на другому – 1,2 %, а на третьому – 2 %. Визначити імовірність того, що випадково обрана лампочка на складі виявиться справною.

Розв’язок. Нехай подія А – випадково обрана електрична лампочка є стандартною (справної). Висунемо три гіпотези:

B₁ – обрана лампочка надійшла з 1-го заводу, значить

B₂ – обрана лампочка надійшла з другого заводу, отже,

B₃ - обрана лампочка надійшла з 3-го заводу, тому

Події В₁, B₂, B₃ утворять повну групу несумісних подій.

Умовна подія полягає в тому, що обрана лампочка надійшла з i-го заводу і є стандартною. Тоді, використовуючи умови задачі,

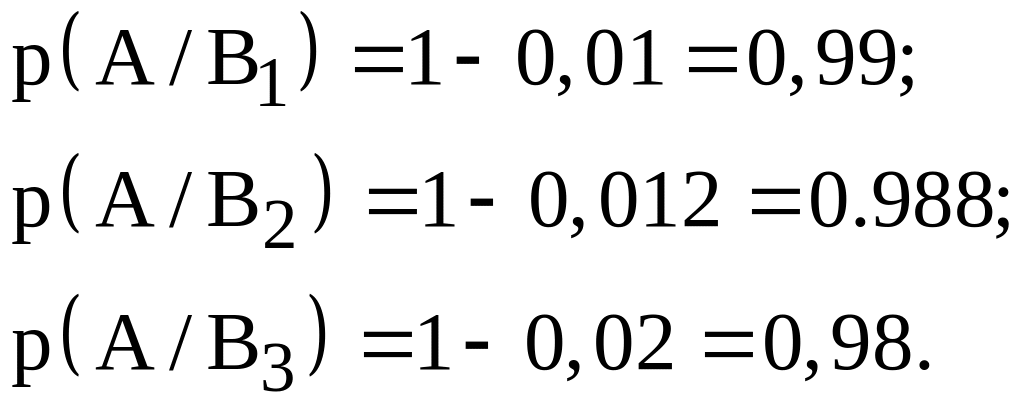
По формулі повної імовірності маємо

2.22 На спостережливій станції встановлені чотири локатори різних конструкцій. Імовірність виявлення цілі за допомогою першого локатора дорівнює 0,86, другого – 0,9, третього – 0,92, четвертого – 0,95. Спостерігач навмання включає один з локаторів. Знайти імовірність виявлення цілі.

Розв’язок. Висунемо чотири гіпотези: В₁ – був включений перший локатор, В₂ – другий, В₃ – третій, В₄ – четвертий. Ці гіпотези утворять повну групу несумісних подій і тому що можливість включення кожного з чотирьох локаторів однакова.

Нехай подія А – ціль виявлена. Тоді подія ціль виявлена i-им локатором і за умовою:

Використовуючи формулу повної імовірності, знаходимо

2.23 Мається вертушка, на якій закріплене шість коробок. У кожній з них утримується набір резисторів (див. таблицю). Резистор, витягнутий випадковим образом з якоїсь коробки, виявився 10-омным. Яка імовірність того, що він був узятий з коробки з номером 6?

Таблиця

Номінальне опір резисторів	Набори резисторів у коробках з номерами						Усього резисторів даного номіналу
	1	2	3	4	5	6
10 Ом	500	0	200	800	1200	1000	3700
100 Ом	300	400	600	200	800	0	2300
1000 Ом	200	600	200	600	0	1000	2600
В С Ь О Г О	1000	1000	1000	1600	2000	2000	8600

Розв’язок. Нехай подія А полягає в тому, що витягнутий випадковим образом резистор виявився 10-Омным. Можна висунути шість гіпотез: Подія (гіпотеза) полягає в тому, що резистор довільного номіналу був витягнутий з коробки з номером Тому що резистор міг бути витягнутий з кожної із шести коробок, то .

Події утворять повну групу несумісних подій.

Введемо умовну подію 10-Омный резистор витягнутий з коробки з номером Тоді, відповідно до приведеної таблиці, маємо:

Шукана імовірність - Для її знаходження скористаємося формулою Байеса

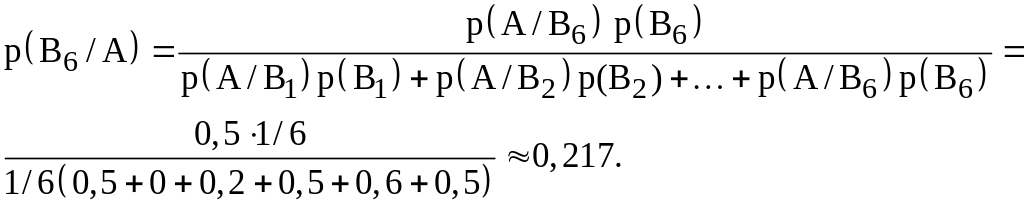
2.24 Кодування повідомлень у цифровій системі зв'язку здійснюється шляхом перетворення їх у послідовність символів 0 і 1. Вплив зовнішніх завад і власного шуму приводить до того, що час від часу при прийомі виникають збої. Відомо, що імовірність прийому 1 при передачі 0 дорівнює 0,08, а імовірність прийому 0 при передачі 1 дорівнює 0,05. Відомо також, що в середньому при передачі повідомлень 0 і 1 складають співвідношення 2:3. Визначити імовірність того, що переданий 0 буде прийнятий правильно.

Розв’язок. Можна висунути тільки дві гіпотези: В₀ – був переданий 0, В₁ – була передана 1. Вони утворять повну групу несумісних подій. А тому що при передачі повідомлень 0 і 1 складають співвідношення 2:3, то і

Нехай подія А₀ – прийнятий 0, а А₁ – прийнята 1. Тоді, виходячи з умови задачі, можна записати наступні умовні імовірності: імовірність прийому 0 при передачі 0 і імовірність прийому 0 при передачі 1. Подія – переданий 0 прийнято правильно. Для знаходження імовірності цієї події скористаємося формулою Байеса:

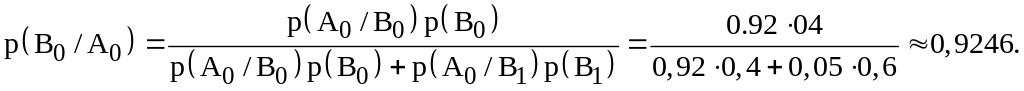
2.25 За даними технічного контролю в середньому 2 % виготовлених на заводі телевізорів мають потребу в додатковому регулюванні. Чому дорівнює імовірність того, що із шести зроблених телевізорів чотири мають потребу в додатковому регулюванні?

Розв’язок. Нехай подія А полягає в тім, що довільно узятий телевізор має потребу в регулюванні. За умовою задачі . Перевірку шести телевізорів можна розглядати як шість випробувань Бернуллі, тому що це повторні незалежні випробування, у кожнім з яких може з'явитися тільки дві події: А – телевізор має потребу в регулюванні і телевізор не має потреби в регулюванні. Імовірність того, що із шести довільно узятих телевізорів чотири мають потребу в додатковому регулюванні, обчислюємо за допомогою формули Бернуллі з :

2.26 Протягом часу Т експлуатується N приладів. Кожний з них має надійність p і виходить з ладу незалежно від інших. Знайти імовірність того, що майстер, викликаний по витіканню часу Т для ремонту несправних приладів, не справиться зі своєю задачею за час t, якщо на ремонт кожного з несправних приладів йому потрібен час t₀.

Розв’язок. Нехай ціла частина відносини Майстер не справиться зі своєю задачею, якщо m = n₀ + 1 або або m = N, де m - число несправних приладів із усієї сукупності приладів. Перевірку N приладів можна розглядати як N іспитів Бернуллі з імовірністю події А – прилад несправний – рівної Імовірність того, що з N приладів вийшли з ладу m за час експлуатації Т знаходимо по формулі Бернуллі:

Подія В – майстер не справився зі своєю задачею за час t – рівнозначно тому, що m дорівнює або N. Тому

2.27 Телефонний зв'язок з 12 абонентами, що знаходяться у вилученому населеному пункті, забезпечується бездротовим зв'язком за допомогою багатоканальної НВЧ-лініі. Кожний з абонентів користується цією лінією протягом 20 % часу пікового навантаження. Скільки каналів потрібно мати, щоб у піковий період лінія була доступна всім абонентам протягом 90 % часу.

Розв’язок. Тому що абонент у піковий період використовує лінію протягом 20 % часу, то імовірність того, що йому буде потрібно в цей період лінія, дорівнює p = 0,2. Природно вважати, що виклики абонентів незалежні. Імовірність того, що лінія буде потрібно одночасно рівно абонентам, у піковий період може бути знайдена за допомогою формули Бернуллі, тому що послідовні іспити полягають у перевірці – пішов або не пішов виклик від кожного з 12 абонентів – з імовірністю виклику p = 0,2. Імовірність того, що лінія буде потрібно одночасно не більш m абонентам, дорівнює

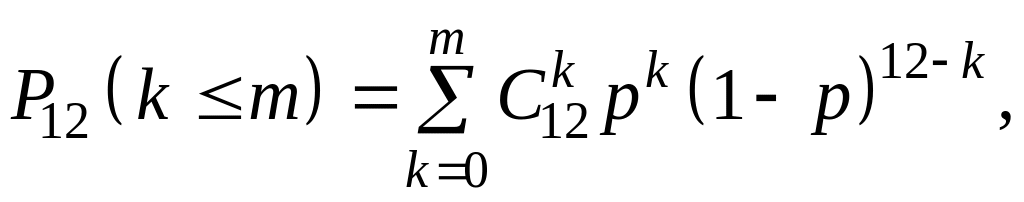
де p = 0,2.

Будемо послідовно обчислювати ці імовірності для m, починаючи з одиниці:

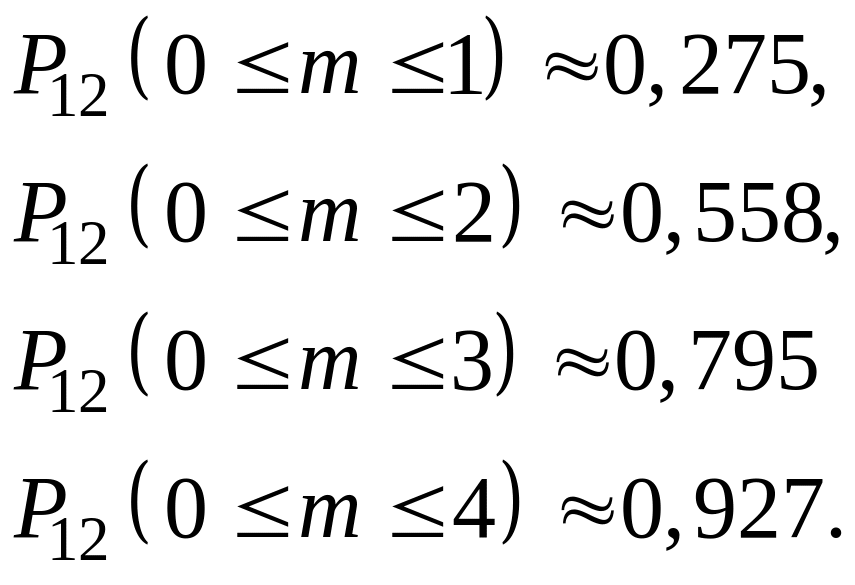
Звідси видно, що з імовірністю 0,927 (92,7 % часу) лінія зв'язку буде потрібно не більш 4 абонентам. Виходить, досить мати 4 канали.

2.28 У лінії зв'язку при передачі повідомлення імовірність похибки одного знака дорівнює 0,01. Знайти імовірність того, що в повідомленні з 1000 знаків утримується не більш трьох похибок.

Розв’язок. Нехай подія А – у повідомленні 1000 знаків утримується не більш трьох похибок. Цю подію можна представити як суму чотирьох несумісних подій:

де подія полягає в тому, що при передачі 1000 знаків у повідомленні маємо k похибок

Перевірку 1000 знаків на наявність похибок можна розглядати як 1000 іспитів Бернуллі з імовірністю появи події (похибки знака) p = 0,01. Тому

Тому що n=1000>>1, p=0,01<<1 і то імовірність в останній формулі можна обчислювати по формулі Пуассона з :

У кінцевому результаті одержуємо

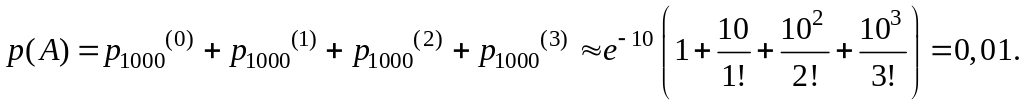
2.30 Виготовлювач радіоелектронного устаткування закуповує 1000 інтегральних схем, кожна з яких з імовірністю 0,2 може виявитися несправною. Визначити імовірність того, що кількість несправних мікросхем буде не менше 200, але не більш 220 штук.

Розв’язок. Імовірність того, що рівно k бракованих мікросхем знаходиться в партії з 1000 штук мікросхем, знаходимо по формулі Бернуллі:

де p = 0,2, а q= 0,8. Тому що число бракованих мікросхем повинне знаходитися між 200 і 220 штуками, то шукана імовірність

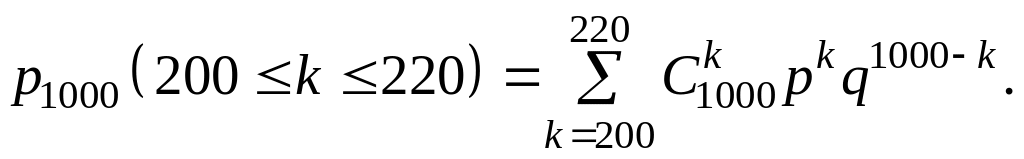
З огляду на те, що k≥200>>1 і npq=160>>1, при обчисленні шуканої імовірності скористаємося інтегральною формулою Муавра-Лапласа:

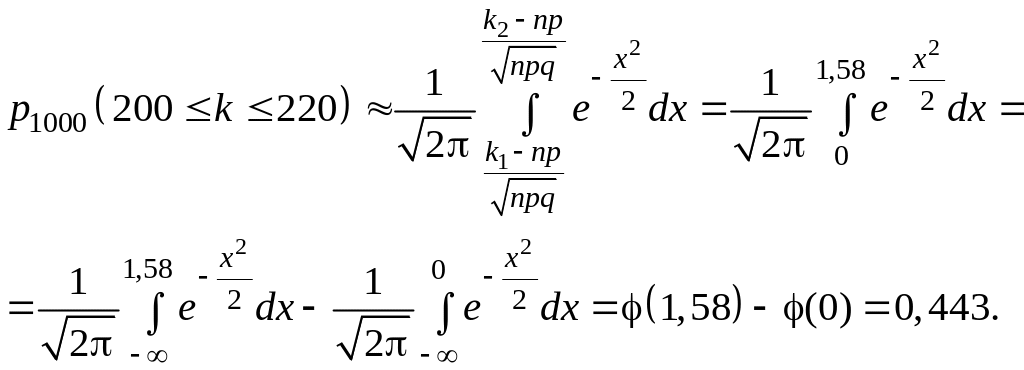
Тут використовувалися табличні значення функції