4.2.2 Задачі

4.30 Прямокутні координати випадкової точки – нормальні випадкові величини з параметрами , і , . Знайти густину імовірності координат цієї точки, якщо

, .

Яким законам розподілу підпорядковуються і ?

4.31. Два резистора з’єднані послідовно. Відомо, що опори резисторів є незалежними випадковими величинами X i Y рівномірно розподіленими відповідно в інтервалах , Знайти густину імовірності загального опору.

4.32. Знайти густину імовірності випадкової величини Z=X+Y, де X i Y – незалежні випадкові величини, густини імовірності яких задані формулами:

де

4.33. Випадкова величина Х підпорядковується нормальному закону розподілу з параметрами Y – рівномірному закону розподілу з параметрами Знайти густину імовірності випадкової величини Z=X+Y, якщо X i Y незалежні.

4.35. Нехай X i Y – незалежні випадкові величини відповідно з густинами імовірності

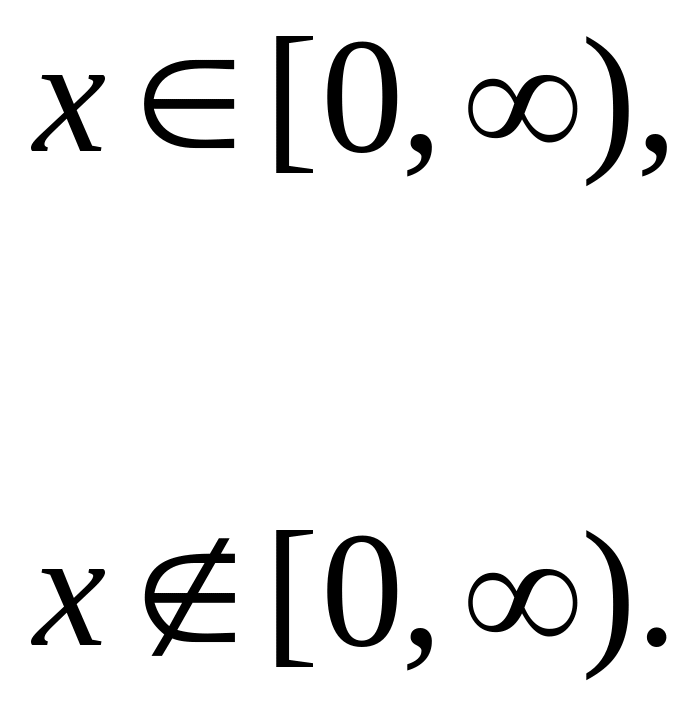
Знайти густину імовірності випадкової величини Z=X+Y.

5. Випадкові процеси

Випадковий процес представляє собою таку функцію часу (або другої змінної), яка в наслідок експерименту може прийняти той чи інший конкретний вигляд, до експерименту невідомий. Іншими словами, випадковий процес – це випадкова функція. Випадкові процеси позначаються прописними латинськими літерами: X(t), Y(t), Z(t),…, де t – аргумент випадкової функції.

Окрема функція, одержана в наслідок експерименту, носить назву реалізації випадкового процесу. Реалізації процесів будемо позначати малими латинськими літерами x(t), y(t), z(t),…

Якщо зафіксувати аргумент t випадкового процесу X(t), то випадковий процес перетворюється у випадкову величину X(t), яка носить назву перерізу випадкового процесу.

Випадковий процес, неперервний або дискретний, якщо відповідно його реалізації мають неперервну структуру (неперервні функції) або мають тільки розриви (стрибки).

Випадковий процес можна розглядати або як сукупність реалізацій процесу, або як сукупності його перерізів, які залежать від параметру t.

Одновимірною функцією (густиною) розподілу випадкового процесу X(t) називається функції розподілу його перерізу X(t):

.

Двовимірною функцією (густиною) розподілу випадкового процесу X(t) називається функція розподілу системи двох його перерізів (X(t₁), X(t₂)):

F1(x;t) = p (X(t₁)<x_1, X(t₂)<x₂) .

Якщо проміжок часу між моментами t₁ і t₂ достатньо малий, то випадкові величини X(t₁) та X(t₂) будуть залежними й у границі t₁ → t₂ збігаються.

Якщо ж |t₁ - t₂| → ∞, то статистичний зв’язок між X(t₁) та X(t₂) має, як правило, послаблюватися, і ці величини стають незалежними, тобто

Математичним сподіванням випадкового процесу X(t) називається невипадкова функція m_x(t), яка при кожному фіксованому значенню t дорівнює математичному сподіванню перерізу X(t):

Математичне сподівання m_x(t) ще носить назву невипадкової компоненти процесу, а різниця - флуктаційної компоненти.

Дисперсією випадкового процесу X(t) називають невипадкову функцію D_х(t), яка при кожному фіксованому значенні аргументу t дорівнює дисперсії перерізу X(t):

Дисперсія випадкового процесу характеризує ступінь відхилення реалізацій відносно математичного сподівання. Її ще позначають

Величину _х(t) називають середнім квадратичним відхиленням або стандартом процесу X(t).

Кореляційною (точніше, автокореляційною) функцією випадкового процесу X(t) називається невипадкова функція двох аргументів R_x (t_1, t₂), яка при кожній парі значень аргументу t_1, t₂ дорівнює кореляційному моменту відповідних перерізів процесу:

R_x (t_1, t₂) = M

При t₁ = t₂ = t кореляційна функція перетворюється у дисперсію випадкового процесу:

Властивості кореляційної функції:

1)R_x(t₁, t₂) = R_x(t₂, t₁) – симетричність;

2)|R_x(t₁, t₂)| ≤ _х(t₁) _х(t₂);

3)функція R_x(t₁, t₂) – позитивно визначена, тобто

де (t) і D відповідно будь-яка функція та будь-яка область інтегрування.

Нормальною кореляційною функцією випадкового процесу X(t) називається функція

тобто коефіцієнт кореляції перерізів X(t₁) та X(t₂) (ρ_х(t, t) = 1).

Якщо на випадковий процес діє деяке перетворення А, то одержуємо другий випадковий процес

Y(t) = A [X(t)]

Перетворення А називається лінійним однорідним, якщо

A [c₁X₁(t) + c₂X₂(t)] = c₁A[X₁(t)] + c₂A[X₂(t)] (c₁, c₂ = const)

Взаємною кореляційною функцією R_xу (t₁, t₂) двох випадкових процесів

X(t) і Y(t) називається функція

R_xу (t₁, t₂) = M .

За визначенням взаємної функції слідує, що

R_xу (t₁, t₂) = R_xу (t₂, t₁).

Нормованою взаємною кореляційною функцією двох випадкових процесів X(t) і Y(t) називається функція

Випадкові процеси X(t) і Y(t) називають некорельованими, якщо

R_xу (t₁, t₂) ≡ 0 (t₁, t₂ є (-∞; ∞)).

Якщо

( ),

де X₁(t), X₂(t),…, X_n(t) – некорельовані випадкові процеси, то

.

Стаціонарним випадковим процесом X(t) (точніше, стаціонарним в широкому розумінні) називається процес, у якого постійне математичне сподівання (m_x(t) = const), а кореляційна функція залежить тільки від різниці між своїми аргументами (R_x(t₁, t₂) = R_x(τ), τ = t₂ - t₁).

Властивості кореляційної функції R_x(τ) зберігаються:

1)R_x(τ) = R_x(-τ) – функція парна;

2)R_x(τ)|≤ R_x(0) = _х²

Проміжок часу τ₀ , протягом якого кореляція між значенням процесу суттєво послаблюється, називається інтервалом кореляції. Існує декілька способів опису інтервалів кореляції τ₀:

1)R_x(τ₀) = ;

2)R_x(τ₀) = ;

3)τ₀ =

4)τ₀ =

Стаціонарний випадковий процес X(t) називається ергодичним процесом, якщо для будь-якої функції його перерізів у (X(t₁), X(t₂),…, X(t_n)) з ймовірністю в одиницю, середнє за часом співпадає з середнім по ансамблю реалізацій

,

де

,

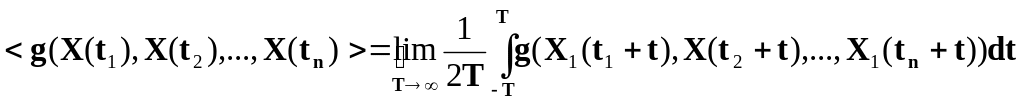Тут - - вимірна густина. Іншими словами, це такі стаціонарні процеси, імовірностну динаміку яких можливо проаналізувати шляхом досліду тільки однієї типової реалізації.

Для ергодичних процесів середнє за часом для однієї реалізації, як і середнє по ансамблю реалізацій для математичного сподівання і кореляційного моменту дають одну і ту ж величину:

,

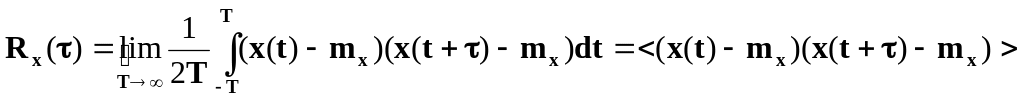де - реалізація випадкового процесу .

Достатньою умовою ергодичності стаціонарного процесу є умова

Якщо випадковий процес описує флуктуації струму у колі або напруги на якомусь опорі, то дисперсія має зміст потужності на одиничному опорі, для якої виконується рівність

або

Функція носить назву двостороневої, а - просто спектральної густини потужності випадкового процесу . Спектральна густина показує, як потужність процесу розподілена по частотам.

Функція має властивості:

1) - парна функція;

2) ;

Густина процесу пов’язана з кореляційною функцією за допомогою формули Вінера-Хінчіна:

,

. (3.1)

Важлива властивість виявляється для ергодичних процесів без конкретизації вигляду для достатньо низьких частот, оскільки при великому часі функція швидко спадає до нуля:

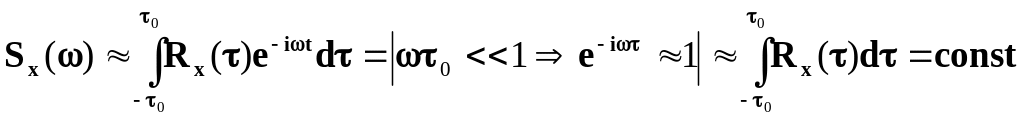
Таким чином, на низьких частотах спектральна густина - величина стала (не залежить від )

Випадковий процес зі сталою спектральною густиною для всіх частот

називається білим шумом за аналогією до білого кольору, який утворюється внаслідок змішування електромагнітних хвиль із приблизно однаковою інтенсивністю у досить широкому діапазоні частот.

Із (3.1) випливає вираз для кореляційної функції білого шуму:

Таким чином, білий шум – дельта – корельваний процес: перерізи процесу у будь-якій близькі моменті, розділені проміжком , не корелюють між собою.