4.2. Функціональне перетворення системи випадкових величин.

Нехай система двох випадкових величин (Y₁,Y₂) - результат функціонального перетворення системи (Х₁,Х₂) з густиною розподілу заданого функціями

здійснюючого взаємно однозначне відображення. У цьому випадку густина розподілу системи випадкових величин (Y₁,Y₂) обчислюється за формулою

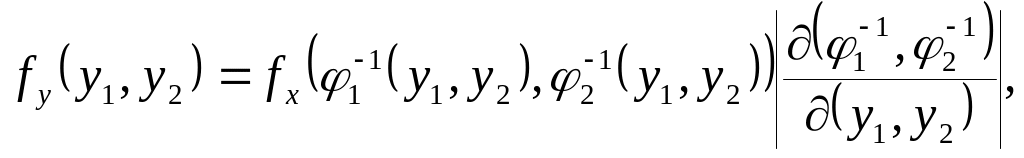
де 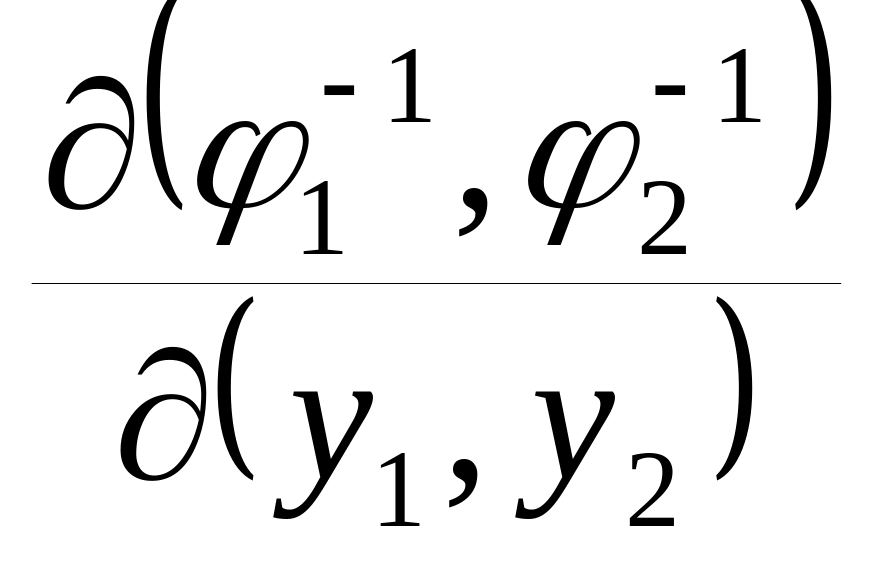- якобіан перетворення системи випадкових величин (Х₁,Х₂) у систему випадкових величин (Y₁,Y₂):

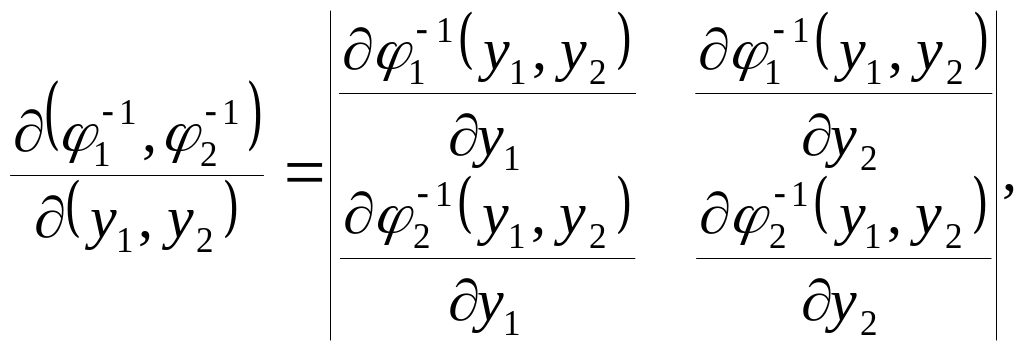
а і - функції, обернені стосовно функцій і .

У загальному випадку, якщо відомо взаємно однозначне відображення

системи n випадкових величин з густиною розподілу в систему то густина розподілу останньої дорівнює

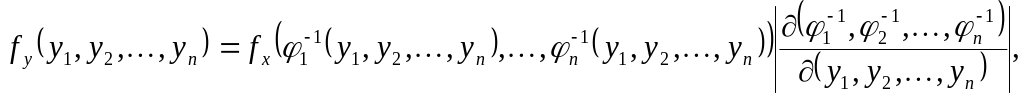
де

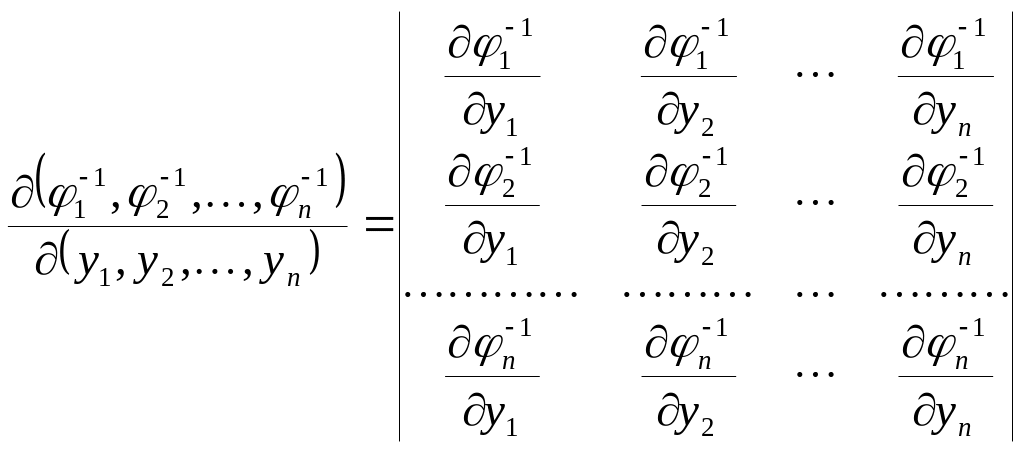
- якобіан перетворення.

Для функції декількох випадкових величин

із заданою густиною розподілу системи задачу визначення густини розподілу випадкової величини Y можна спочатку звести до задачі знаходження густини розподілу системи випадкових величин , отриманих за допомогою перетворення:

а потім, користуючись властивістю густини розподілу системи, знайти густину розподілу випадкової величини Y:

Так, у випадку двох змінних:

з густиною розподілу системи , маємо

Звідси густина розподілу суми двох випадкових величин (КОМПОЗИЦІЯ ЗАКОНІВ)

виражається будь-якою з формул

Зокрема, коли випадкові величини - незалежні (f_x(x₁,x₂)= f₁(x₁)f₂(x₂), f₁(x₁) та f₂(x₂)- густини розподілу Х₁ і Х₂), то

або

Нехай Y(t)- випадкова функція часу, що складається з корисного сигналу X(t) та адитивного шуму N(t). При фіксованому моменті часу t значення Y= Y(t) цієї функції являє собою випадкову величину, рівну сумі двох інших

Y=X+N.

Умовну густину розподілу випадкової величини Х за умови, що випадкова величина Y прийняла значення y, знаходимо за формулою Байєса

Тут і - густини розподілу випадкових величин X і Y.

Якщо значення х випадкової величини Х задано, то випадковий характер Y визначається тільки шумовою складовою N. А через те що N = Y-X, то де - густина розподілу шуму N. Вважаючи випадкові величини Х та N незалежними, маємо

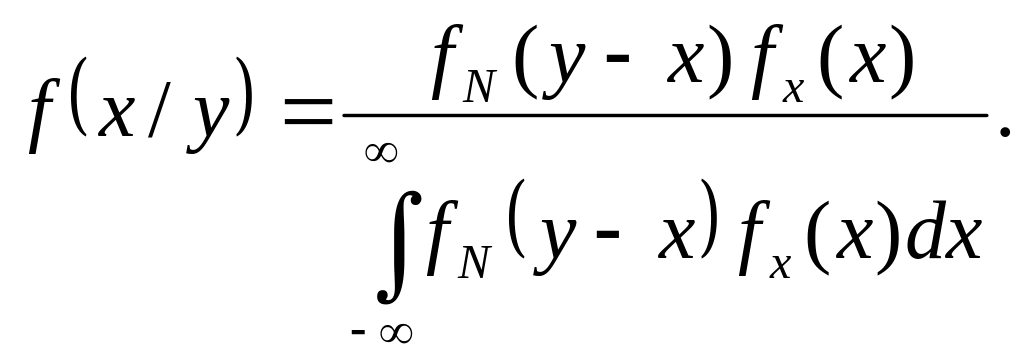
При спостережуваному значенні сигналу те значення х, для якого функція приймає максимальне значення, називається правдоподібною оцінкою значення, що приймається випадковою величиною Х при спостережуваному значенні випадкової величини Y.

4.2.1 Приклади розв’язання задач

4.25. Система двох незалежних випадкових величин X і Y, розподілених за нормальним законом з параметрами m_x=m_y=0 і визначає випадкову точку на площині прямокутної системи координат.

Знайти густину розподілу положення точки в полярних координатах і .

Розв’язок. Прямокутні координати зв'язані з полярними за допомогою перетворення

якобіан якого

Через те що шуканий розподіл знаходиться за формулою

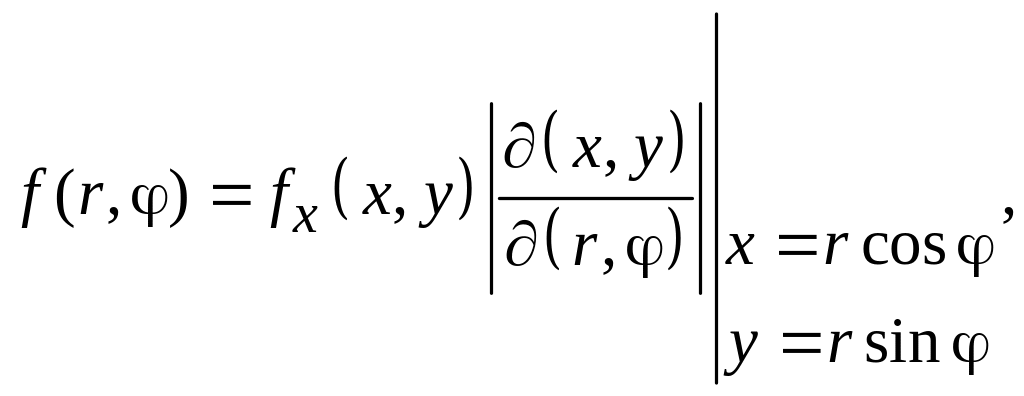
де густина розподілу випадкової точки (X,Y)

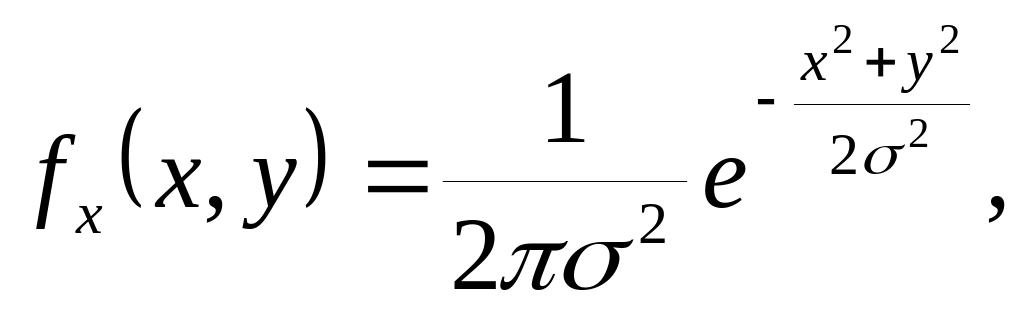
то

Випадкові величини і незалежні, тому що

де

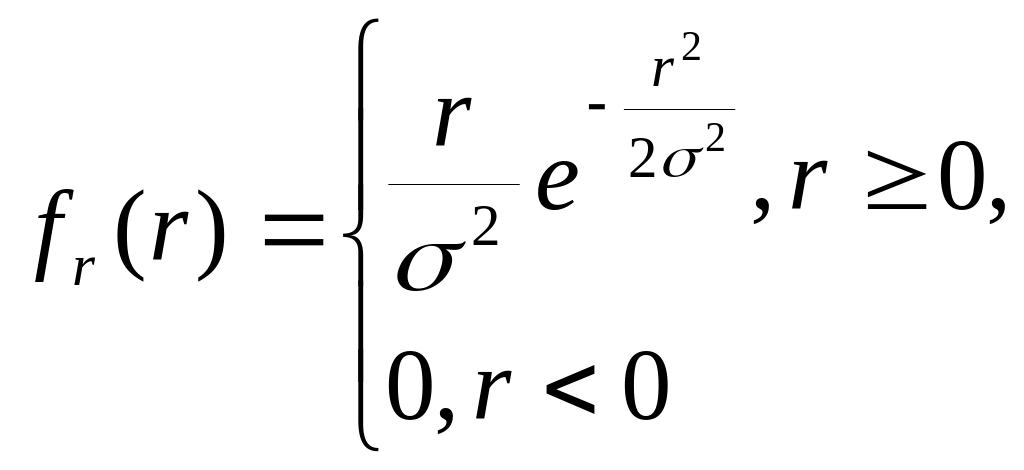- закон Релея і

- закон рівномірного розподілу.

4.26. Три незалежні випадкові величини X, Y і Z, що мають однакові нормальні густини імовірності з параметрами m_x=m_y=m_z=0 і визначають випадкову точку в просторі прямокутної системи координат.

Визначити одновимірну густину імовірності f(r) випадкової величини R, що представляє собою довжину радіус-вектора в сферичній системі координат.