3.2. Безперервні випадкові величини

Безперервна випадкова величина – це величина, що у результаті проведення експериментів суцільно заповнює кінцевий або нескінченний інтервал.

Змішана випадкова величина – це величина, що у результаті проведення експериментів приймає кінцеву або рахункову безліч значень, а також суцільно заповнює кінцевий або нескінченний інтервал.

Функцією розподілу безперервної випадкової величини Х називається функція F(x), рівна імовірності того, що в результаті проведення експерименту випадкова величина Х прийме значення менше чим X:

F(x) = p(X<x).

Густиною розподілу безперервної випадкової величини Х називається функція f(x) яка рівна похідній від функції розподілу:

Вона характеризує локальний розподіл імовірності випадкової величини і є більш інформативною, чим функція розподілу.

Властивості густини розподілу:

1) не негативність;

2) умова нормування;

3)

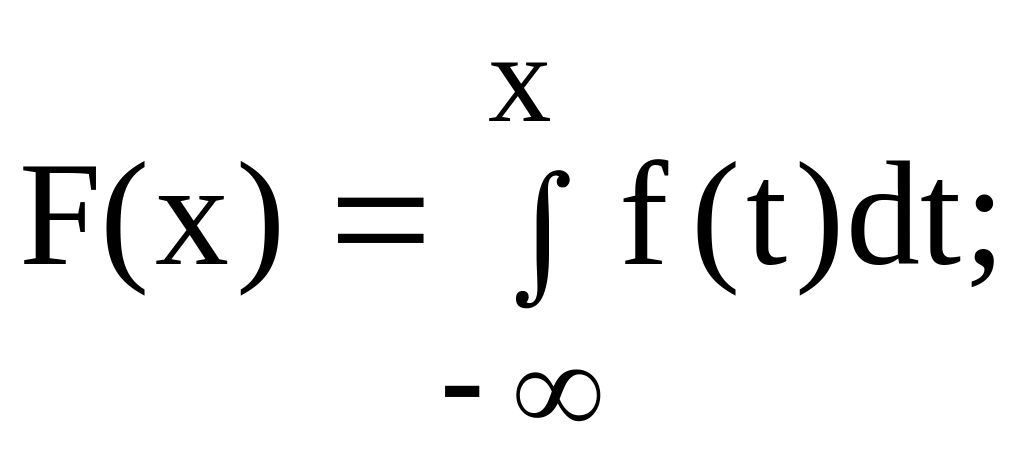
4)

Математичним сподіванням безперервної випадкової величини Х називається її середнє значення, що обчислюється по формулі:

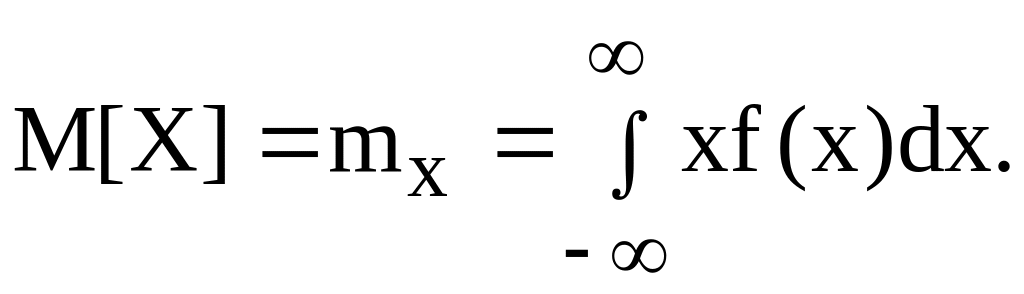
Для змішаної випадкової величини математичне сподівання виражається сумою двох додатків:

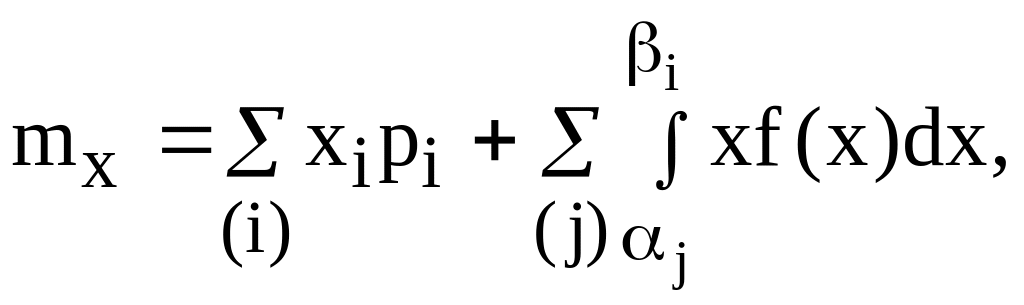(2.1)

де перша сума поширюється на всі крапки розриву функції розподілу, а друга – на всі ділянки її безперервності.

Дисперсія безперервних і змішаної випадкових величин обчислюється відповідно по формулах:

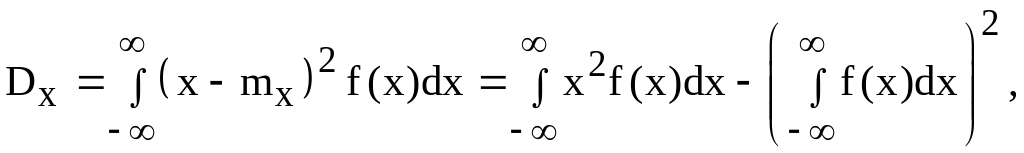
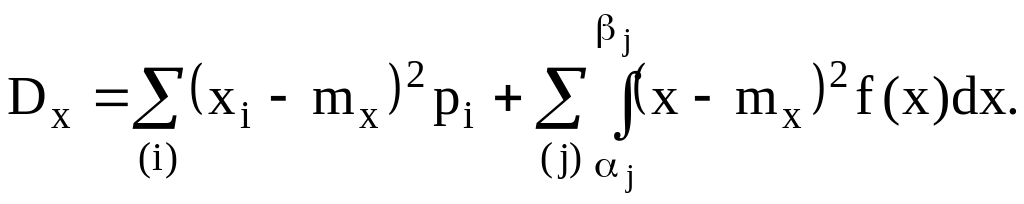
Густини розподілу основних випадкових величин:

1) 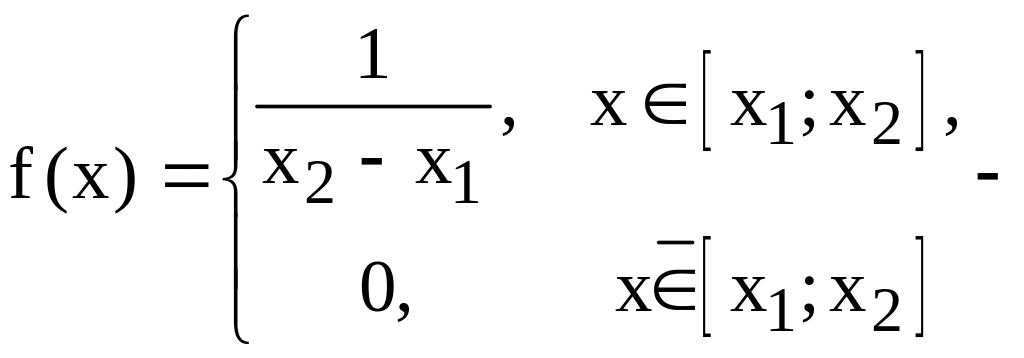рівномірний розподіл,

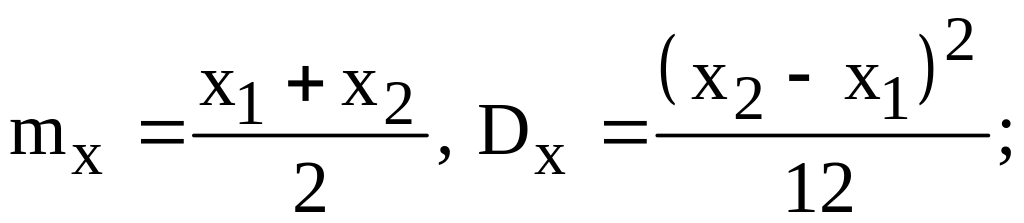
2) 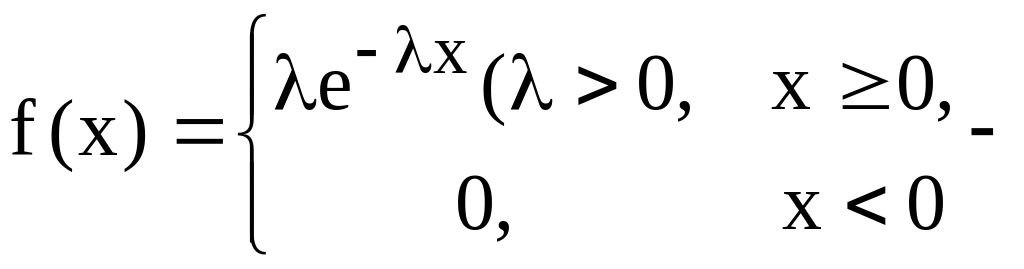показовий (експонеційний) розподіл,

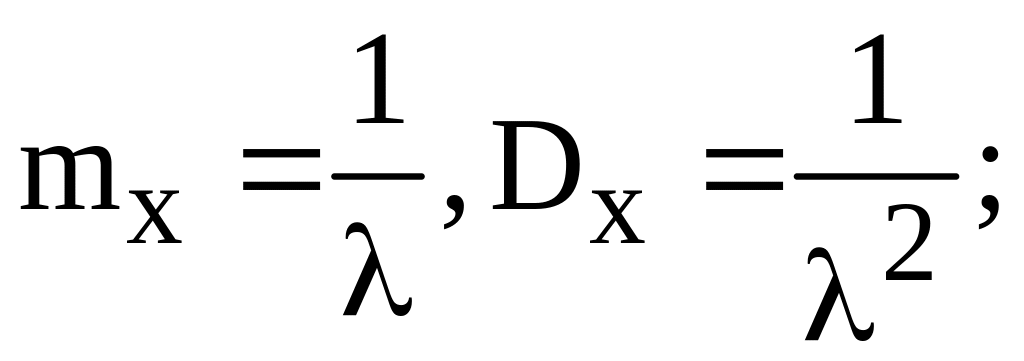
3) 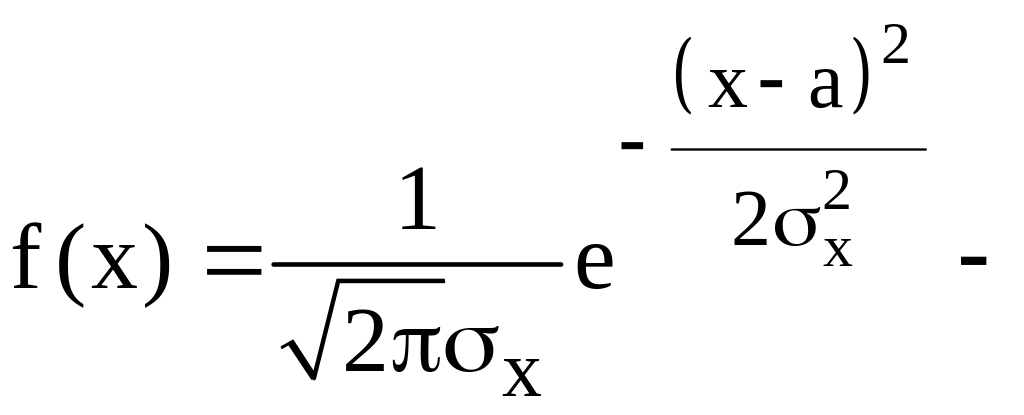нормальний (гауссовський) розподіл,

4)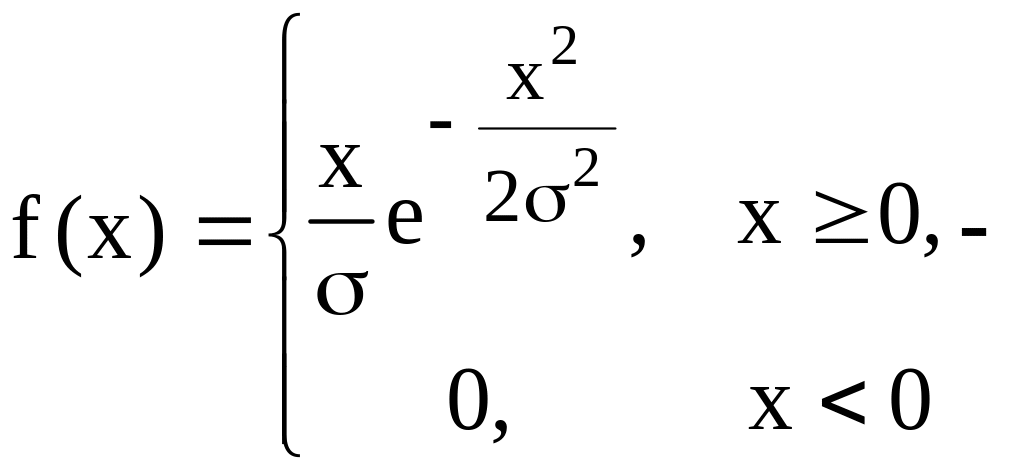 розподіл Релея, ;

5) 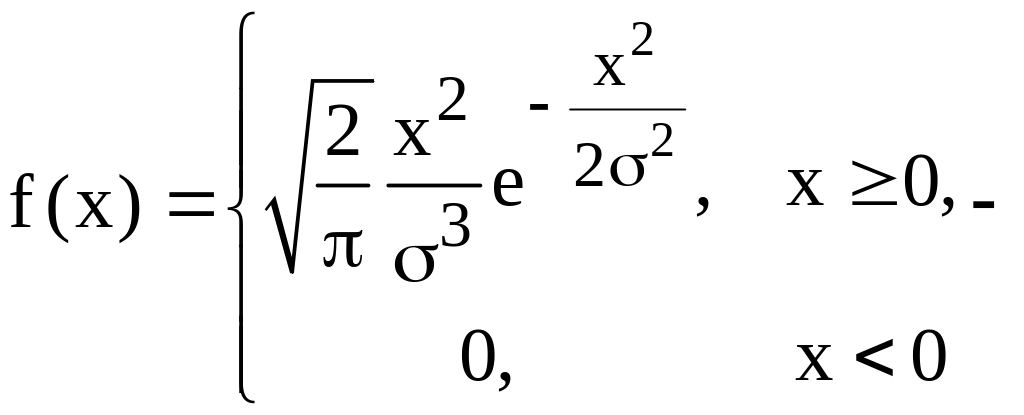розподіл Максвелла,

6) 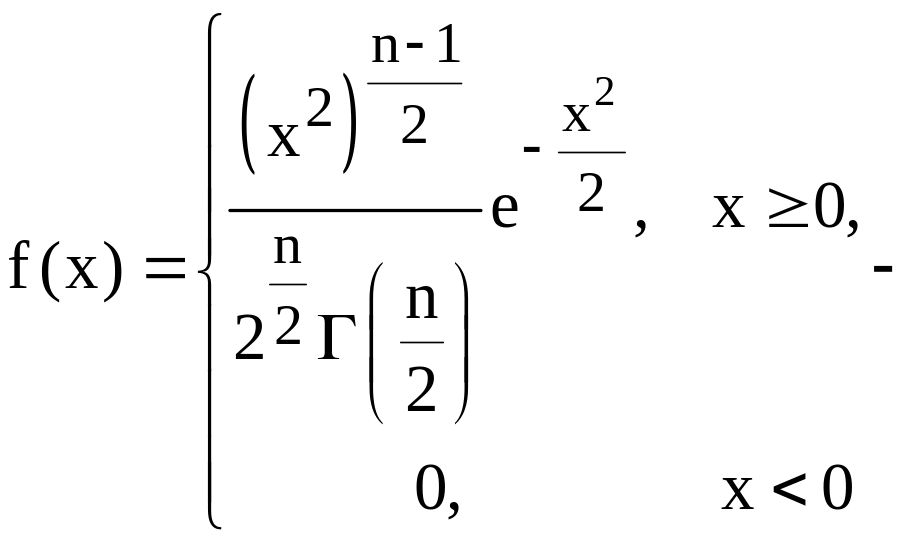хі – квадратичний розподіл, де G(n) – гамма-функція:

і

3.2.1. Приклади розв’язання задач

3.13. Густина імовірності випадкової величини Х задана в такий спосіб:

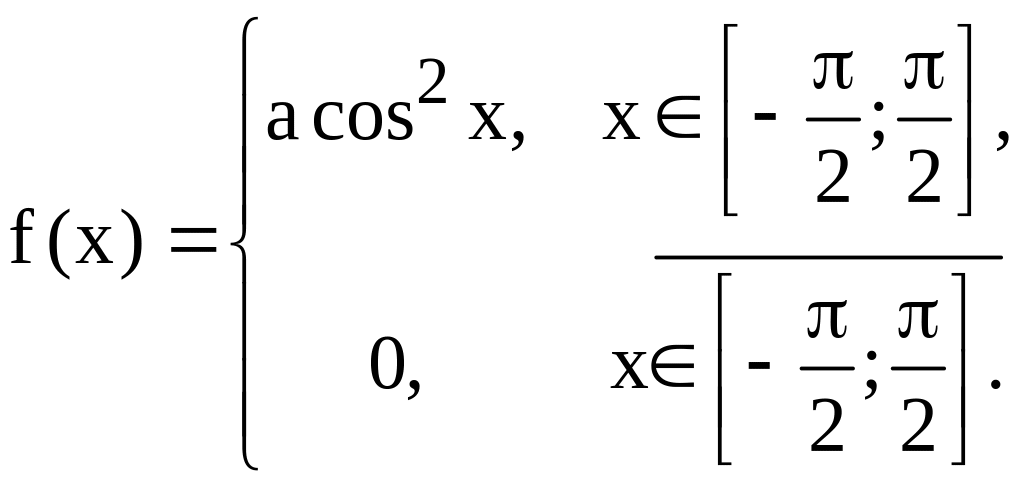
Знайти:

1)коефіцієнт a;

2)функцію розподілу;

3)імовірність улучення випадкової величини в інтервал

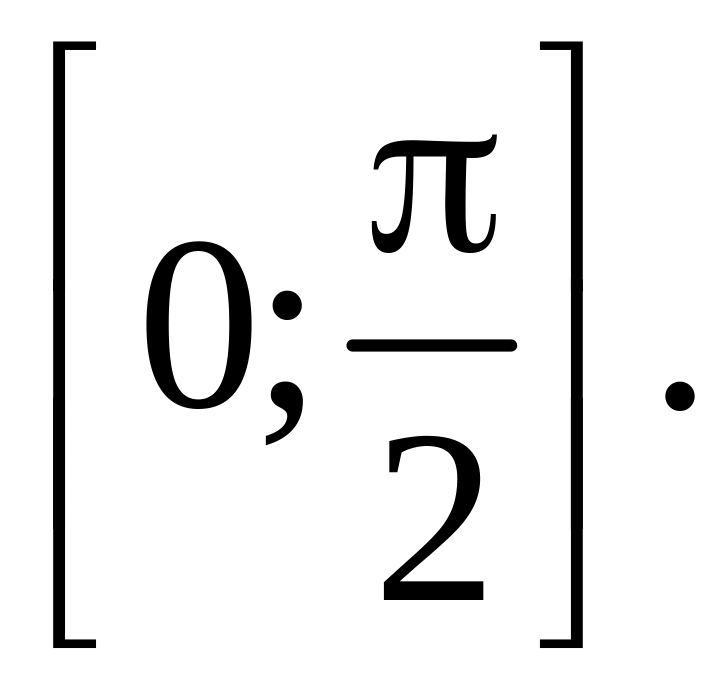
Розв’язок.

1) Коефіцієнт a будемо знаходити з умови нормування густини розподілу:

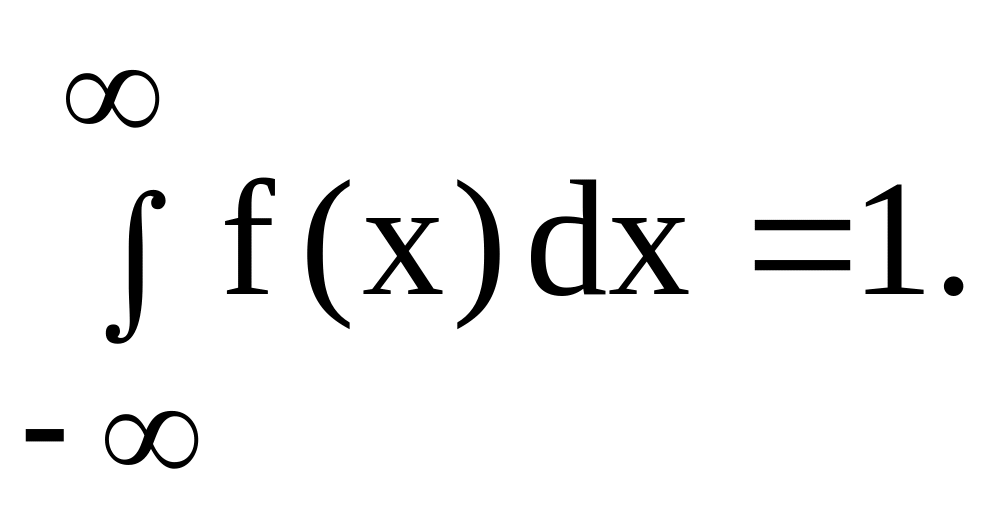
Тоді

Звідси

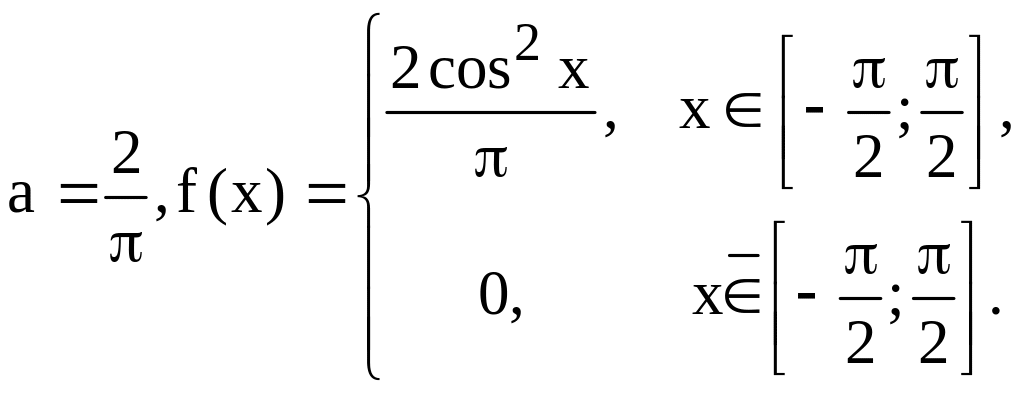
2)Функція розподілу F(x) визначається по формулі

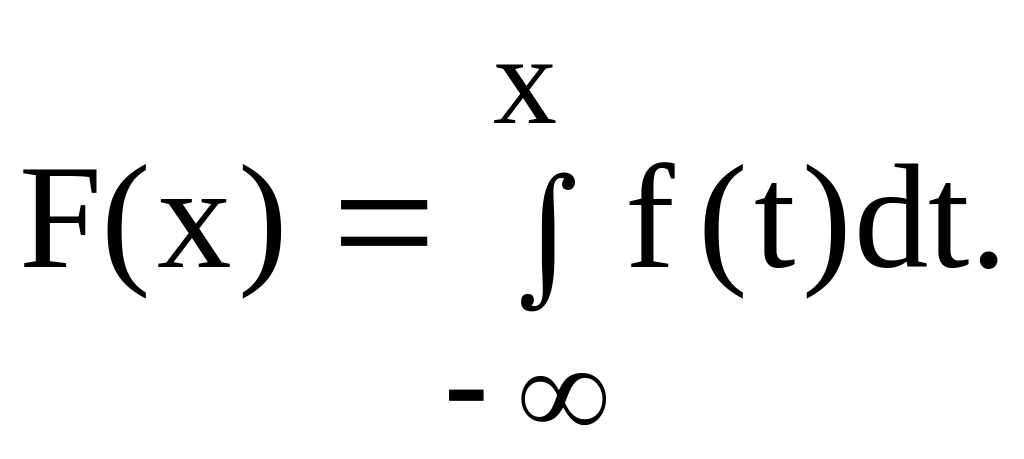
При побудові функції F(x) будемо враховувати, що підінтегральна функція на різних інтервалах має різний вигляд:

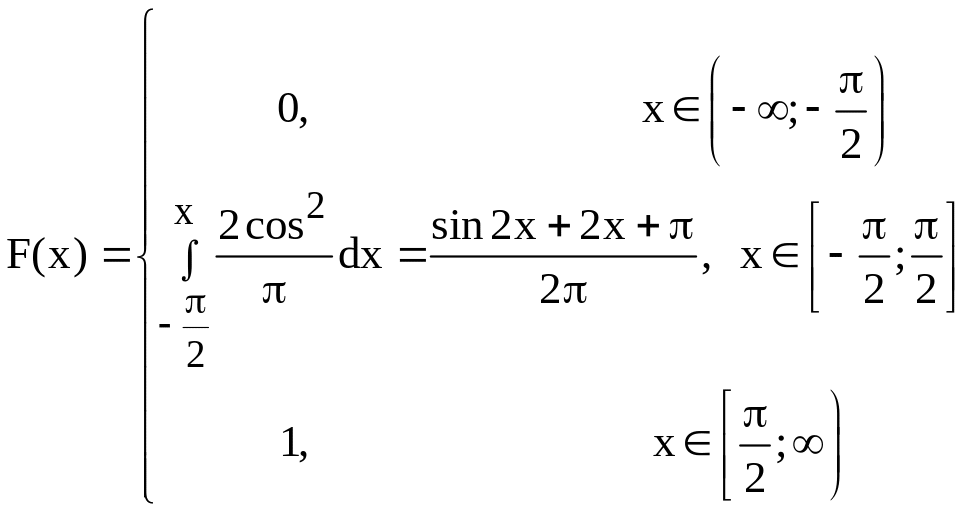
3) Імовірність улучення випадкової величини Х в проміжок 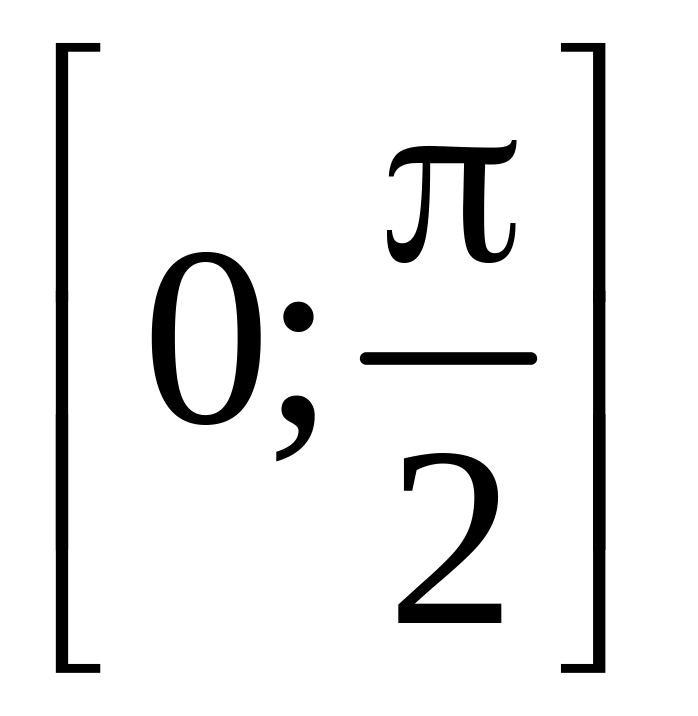обчислюється по формулі

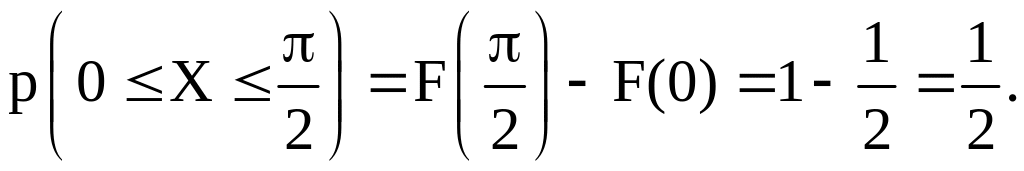
3.14. Вольтамперна характеристика напівпровідникового діода часто описується рівнянням Шоклі

де U – напруга, прикладена до діода, зворотний струм, h - постійна, залежна від параметрів реального діода, струм, що протікає через діод. Визначити математичне сподівання протікання струму через діод, вважаючи прикладену до нього напругу рівномірно розподіленою на інтервалі [0;1] випадковою величиною при і h = 25.

Розв’язок. Якщо випадкова величина U має густину розподілу f(u) і g(U) – функція випадкової величини U, то математичне сподівання цієї функції

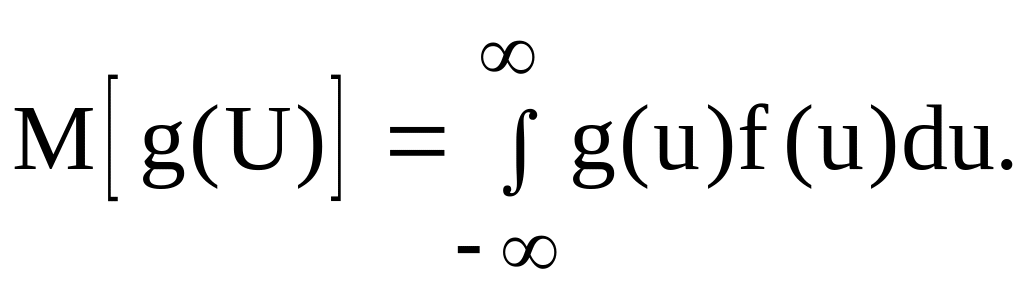
Скористаємося цією формулою при рішенні задачі, вважаючи, що густина розподілу f(u) рівномірно розподілена на інтервалі [0;1]:

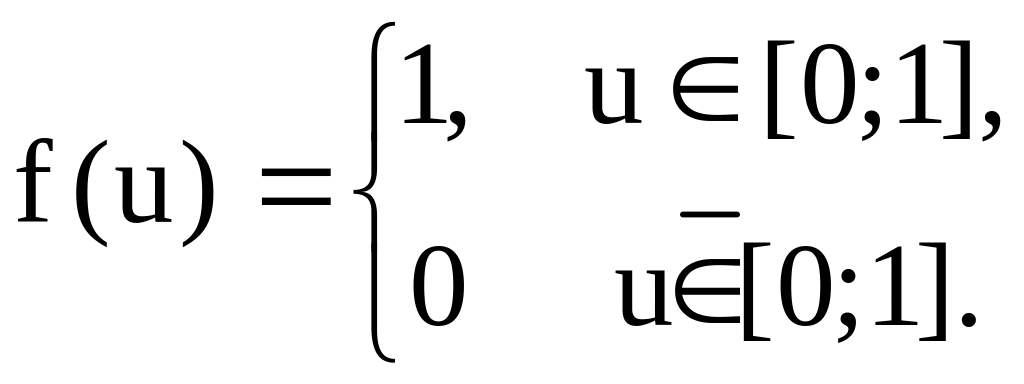
Шукана величина

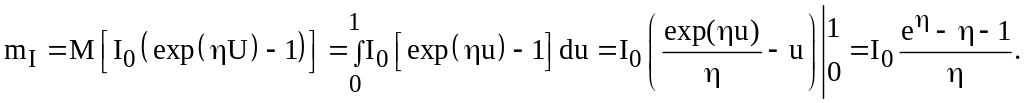
Підставляючи параметри діода і h = 25, остаточно одержуємо =2,88.

3.15. Імовірність того, що випадковий струм з нормальним розподілом прийме значення £ 1 складає 0,5. Крім того, імовірність перевищення їм рівня 5 складає 0,0228. Визначити математичне сподівання і дисперсію цієї випадкової величини.

Розв’язок .Густина імовірності нормально розподіленого випадкового струму

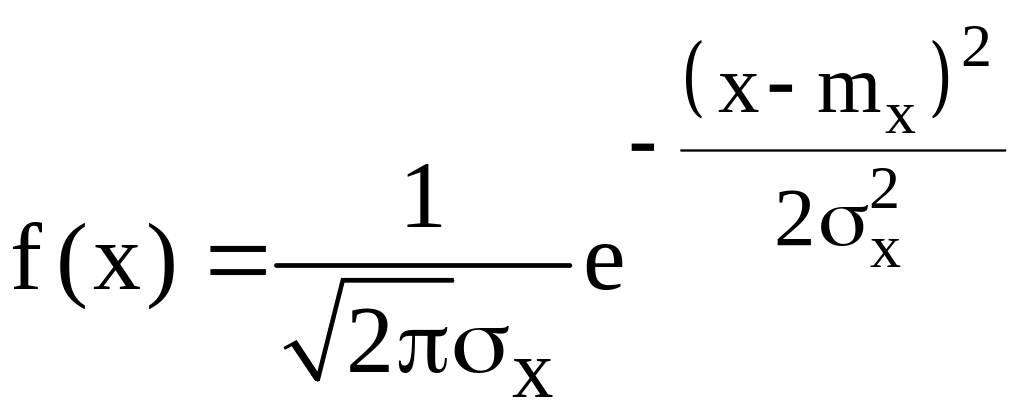
визначається двома параметрами: математичним сподіванням m_x і дисперсією . Для визначення цих величин скористаємося імовірністю, рівної 0,5, того, що випадковий струм C прийме значення £ 1:

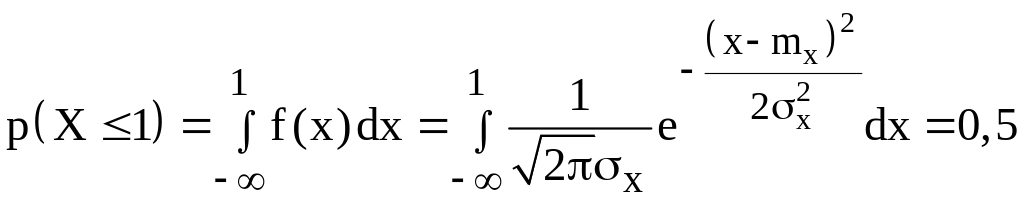
і умовою перевищення значення випадкової величини Х рівня 5 з імовірністю цієї події, рівної 0,0228:

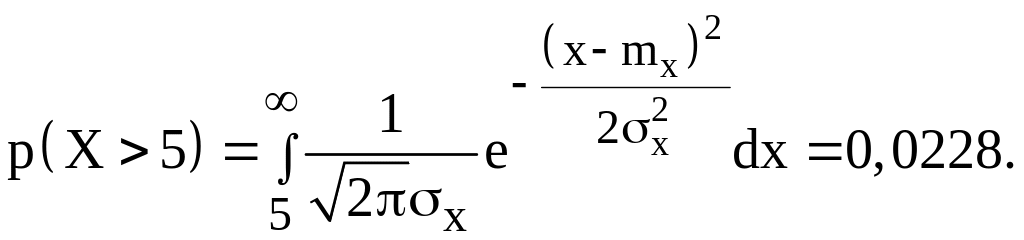
Отже, ми одержали два рівняння з двома невідомими m_x і s_x. Тепер задача полягає в тім, що потрібно вирішити систему двох нелінійних рівнянь із двома невідомими. З цією метою обидва інтеграли в рівняннях приведемо до таблиці значень функції

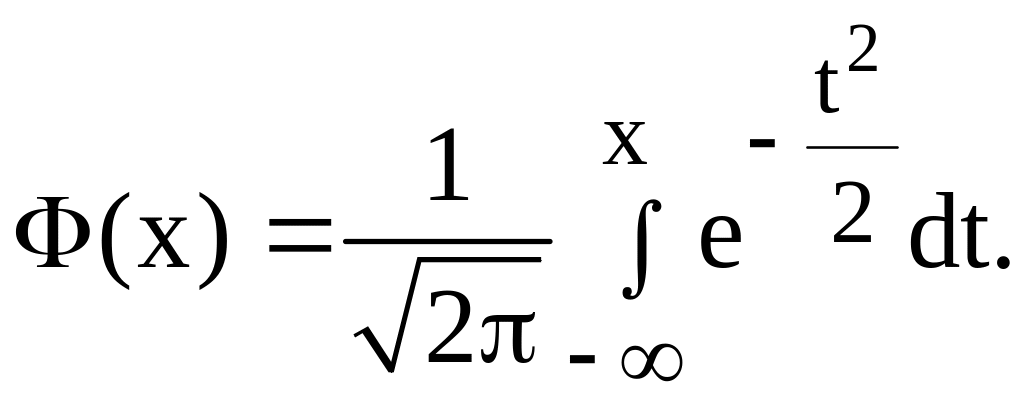
Перепишемо перше рівняння

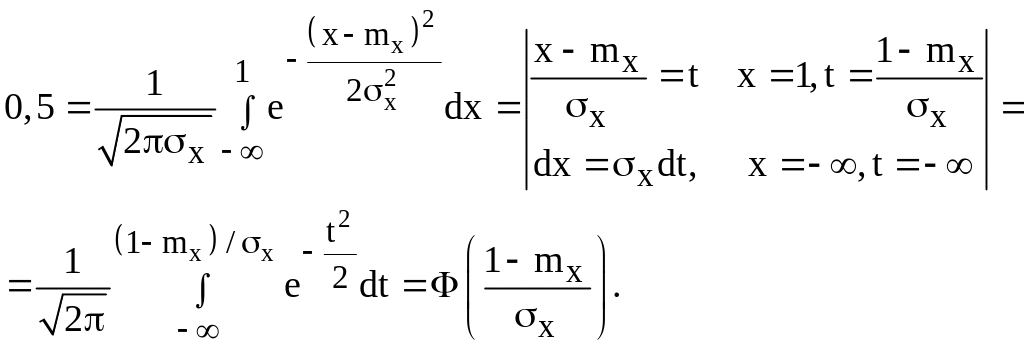
З таблиці значень функції F(х) знаходимо, що F(0) = 0,5. Значить 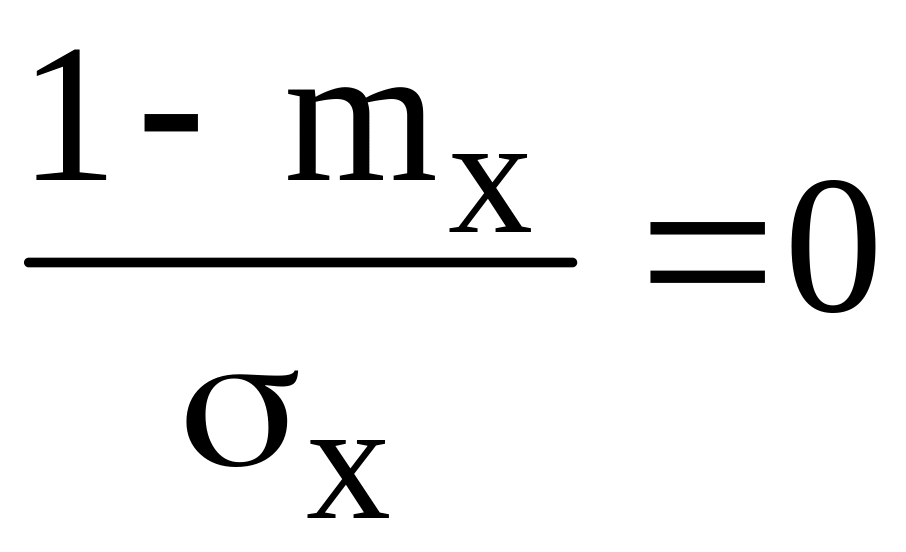і .

Перепишемо друге рівняння скориставшись тією ж заміною перемінної в інтегралі й умовою, що математичне сподівання випадкового струму :

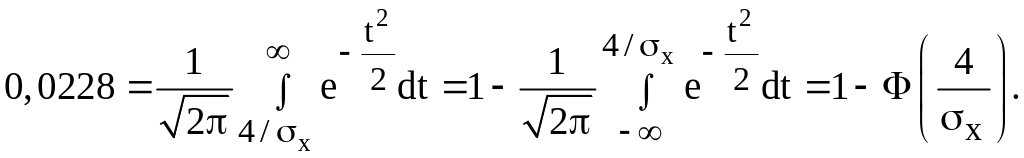
Тут ми скористалися тим, що

З передостаннього співвідношення одержуємо

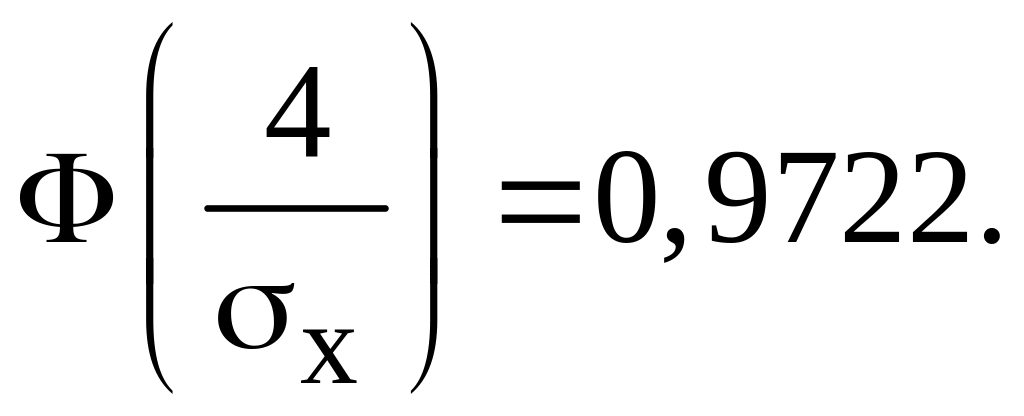
Із таблиці значень функції F(х) знаходимо аргумент Х, при якому F(х) = 0,9722:

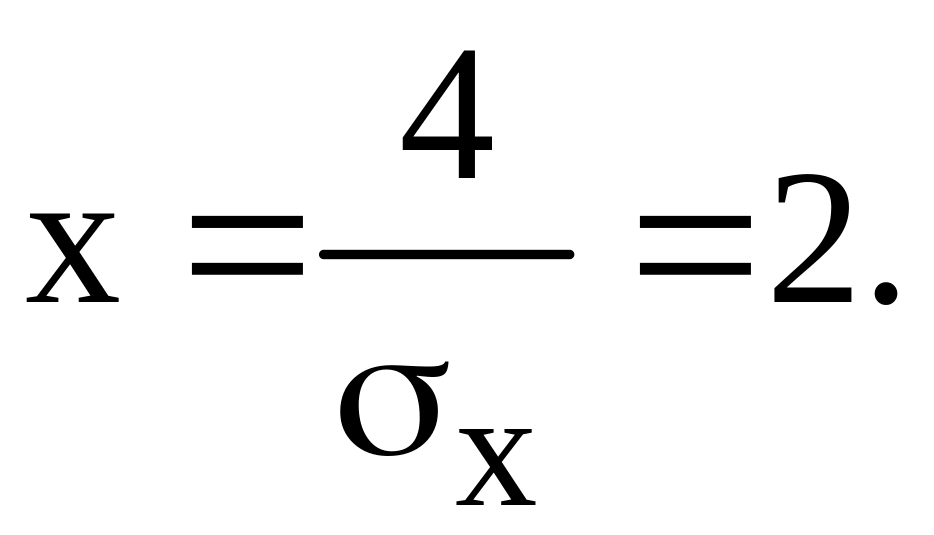
Звідси дисперсія струму

3.16 Розроблювальний супутник зв'язку повинний характеризуватися середнім часом наробітку на відмовлення 5 років. Вважаючи реальний час наробітку на відмовлення випадковою експоненційно розподіленою величиною, визначити умовну імовірність того, що супутник прослужить 10 років і більш – за умови, що він уже відробив 5 років.

Розв’язок. Нехай випадкова величина Т – реальний час наробітку на відмовлення супутника зв'язку. Позначимо через А і В події, що складаються в тім, що:

супутник прослужить 10 років і більш, тобто випадкова величина T прийме значення ³ 10;

супутник відробив 5 років.

Шукану імовірність p(A/B) знаходимо по формулі умовної імовірності:

де

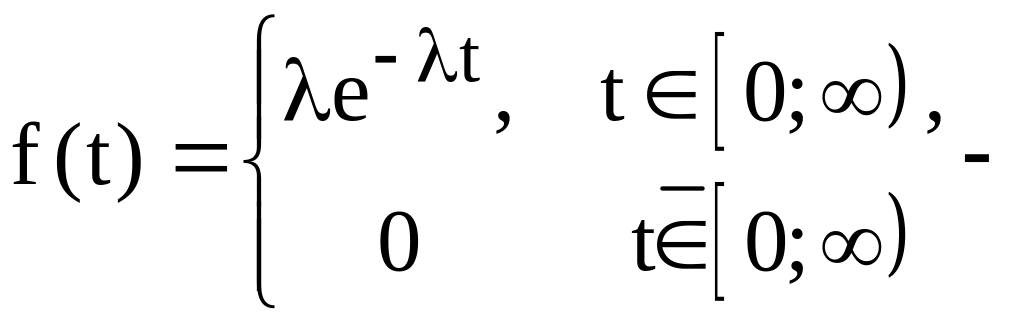
щільність імовірності експоненційно розподіленої випадкової величини Т. За умовою задачі математичне сподівання m випадкової величини Т дорівнює 5. Значить 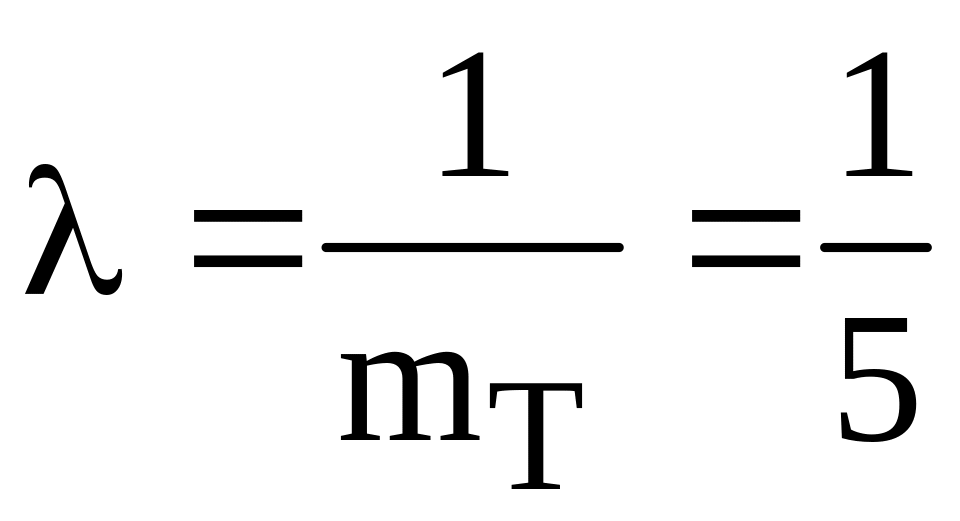і

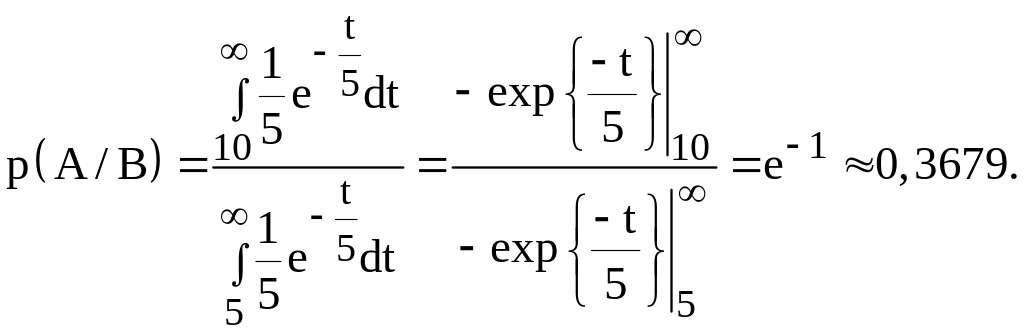
3.17. Зріст дорослих чоловіків є випадковою величиною, розподіленою по нормальному закону. Нехай математичне сподівання її дорівнює 175 см, а середнє квадратичне відхилення – 6 см. Визначити імовірність того, що хоча б один з випадково обраних п'яти чоловіків буде мати зріст від 170 до 180 см.

Розв’язок. Нехай випадкова величина Х – зріст дорослого чоловіка. Густина розподілу цієї випадкової величини має вигляд

Імовірність того, що довільно обраний чоловік має зріст між 170 і 180 см (цю подію позначимо А), тобто, що випадкова величина Х прийме значення між зазначеними величинами, дорівнює

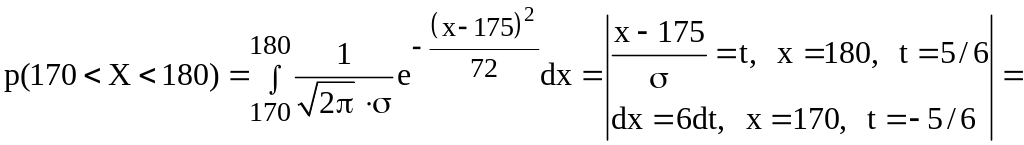
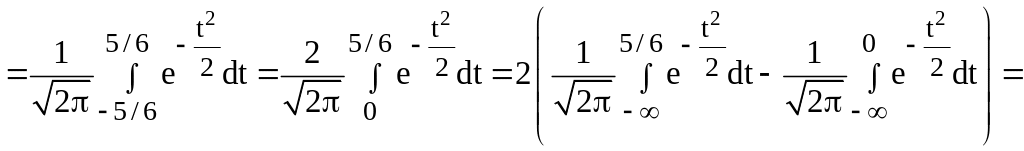
Визначимо імовірність протилежної події А –зріст довільно обраного чоловіка не знаходиться в інтервалі (170;180):

Імовірність того, що хоча б один з випадково обраних п'яти чоловіків буде мати зріст від 170 до 180 см будемо знаходити, виходячи з протилежної події:

3.18. Амплітудна характеристика обмежника має вигляд

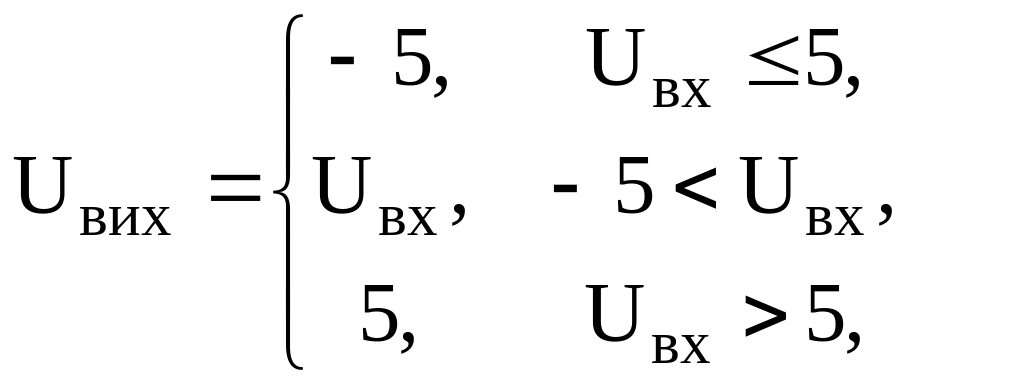
Визначити математичне сподівання вихідного сигналу, вважаючи вхідний сигнал рівномірно розподіленим в інтервалі від –2 до +8.

Розв’язок. Вихідний сигнал для значень вхідного сигналу залишається незмінним = , а для він стає постійним . Це значить, що випадкова величина є змішаною випадковою величиною – безперервної (рівномірно розподіленої на інтервалі ) і дискретної, приймаючи одне значення , на відрізку [5;8]. А тому що вхідний сигнал має густину імовірності

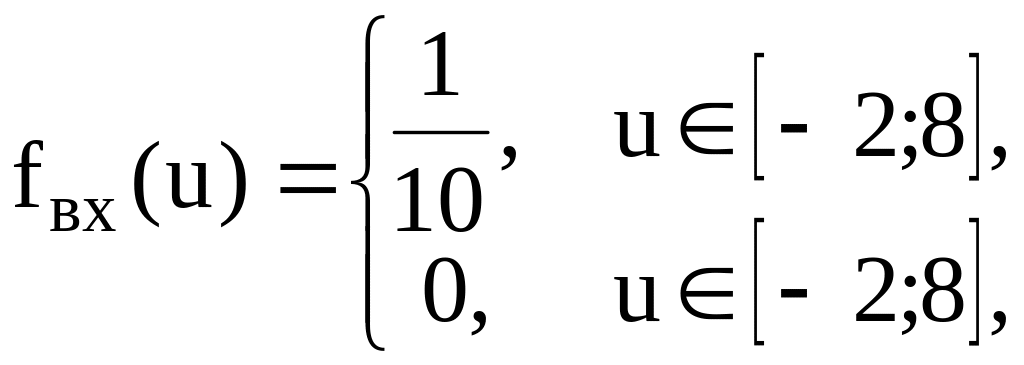
то густина імовірності вихідного сигналу

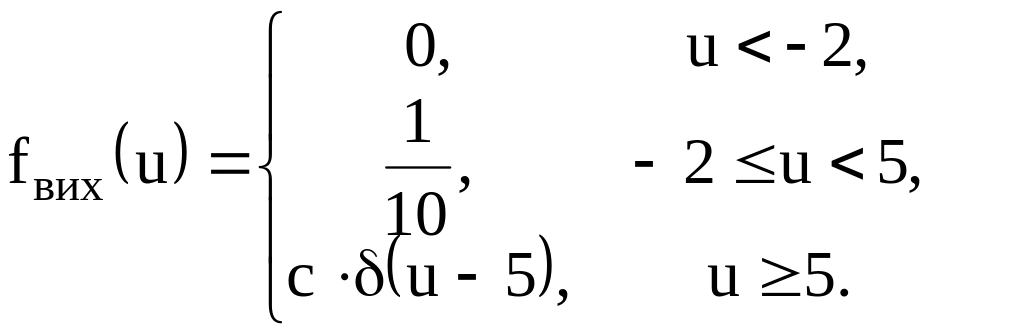
З умови нормування густини імовірності

знаходимо константу с:

яка дорівнює імовірності того, що випадкова величина прийняла значення 5.

Використовуючи формулу (2.1) для змішаної випадкової величини знаходимо математичне сподівання вихідного сигналу