26. Первообразная функции и неопределёный интеграл. Тоерема о сущ-нии первообразной для аналитич. Ф-ии. Ф-ла Ньютона-Лейбница
Опр: F(z) наз-ся первообразной F(z) в Д,еслиF`(z)=f(z) для любой zєД
Опр:
совокупность всех первообразных F(z):
{F(z)+c}
где F(z)-первооб.
f(z)
наз-сянеопределён интеграл f(z):
Т:
Если f(z)
аналитична в обл. Д, z0єД
–фиксир-ая (.)⇒F(z)=
является первообразной для f(z)
и F(z)
аналитична в Д.
Т: Ф-ла Ньютона-Лейбница
Если f(z) аналитична в Д,то справедлива ф-ла Ньютона-Лейбница
= F(z) lz0z , F(z)- первообр. Для F(z)
Спаведлива таблица инт-ов для однознач ф-ий справедлива ф-ла инт-ла по частям
Пр:
l1+i0
= -cos(1+i) +cos0 =
Cosz= (eiz+e-iz)/2
Cos(1+i)= (ei(1+i)+e-i(1+i))/2
ez=ex+yi=e(cosy+isiny)
=-cos(1)ch(1)+isin(1)sh(1)+1
27. Интегрированная ф-ла Коши для ф-ии и для производной
Т1: Если f(z) аналитична в Д и непер-на в Д=ДuαД⇒любойzєД
F(z)=1/2Пi
d
–интегральная ф-ла для ф-ий; обход в +
Т2:Если f(z) непер-на в Д и непер-на в Д, то любой zєД
F(n)(z)=n!/2Пi
d
если существует любой zєДпроиз-аяf(z)
любого порядка
Д-во:
1)
dz
=2Пif(a)
если: 1)f(z)
аналитична в Д; 2) f(z)
непрер-на в Д; 3)aєД
2)
те же условия
= (2Пi/n!)f(n)(a)
Пр:
dz
= C:z-2=4
1)f(z)=z2 – аналитична во всей обл С
2) (.)a=1 єД
n+1=4 n=3
= (2Пi/3!) (z2) lz=1 = 0
28.Ряд Тейлора. Теорема о разложении аналитической ф-ии в ряд Тейлора.Утверждение о радиусе сход-ти ряда Тейлора. Разложения элем ф-ий.
Ряд:
n
=
n+i
n
(1) степенной ряд
n(z-z0)n;
Утв:
Ряд
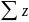n
сход-ся тогда и только тогда, когда
n
и
n
cх-ся
и справедливо рав-во (1)
Утв: Сумма степ. Внутри круга сходимости является аналитической ф-ей
Утв: Любой степ. Ряд внутри круга сходимости является рядом Тейлора своей суммой
f(z)=
n(z-z0)n
(z-z0)<R⇒коэф
степ. Ряда нах-ся однозначно Сn=f(n)(z0)/n!
28.Ряд Тейлора. Теорема о разложении аналитической функции в ряд Тейлора. Утверждение в радиусе сходимости ряда Тейлора. Разложения элементарных ф-ций
Ряд: n=1∞∑zn= n=1∞∑xn + n=1∞∑yn(1)
Степенной ряд: n=0∞∑Cn(z-z0)n
Утв: Ряд ∑zn сходится тогда и только тогда, когда ∑xnи ∑yncходятся и справедливо равенство (1)
Утв: Сумма степ. Внутри круга сходимости является аналитической ф-цией
Утв: Любой степ. ряд внутри круга сходимости явл. Рядом Тейлора своей суммой
f(z)=n=0∞∑Cn(z-z0)n (z—z0) строго меньше R
коэф. Степенного ряда находится однозначно
Сn=f(n)(z0)/n!
Теорема о разложении аналит. Ф-ции в ряд Тейлора
Пусть f(z) аналитична в D, z0∈ D, то в любом круге KR = {z: |(z-z0)| < R } и KR ∈ D, тогда ф-ция f(z) разложится в ряд Тейлора с центром в z0
f(z) = n=0∞∑Cn(z-z0)n, где Cn=f(n)(z0)/n! = =1/2π γ∫ f(ξ)dξ/(ξ-z0)n+1, γ: |(z-z0)|=R
Теорема. Радиус сход.ряда расклад. Аналит ф-цию в ряд Тейлора, равн кротчайшему расстоянию от (.)zдо ближайшей (.)f
C
29. Ряд Лорана ( определение, обл. сходимости). Т-ма Лорана о разложении аналитической в кольце ф-ции в ряд Лорана. Примеры.
Опр. Ряд вида -∞+∞∑ Cn(z-z0)n,z0 –фикс. (.)€ С; Сn, z, z0 € C, наз-ся рядом Лорана
-∞+∞∑ Cn(z-z0)n=n=-∞-1∑ Cn(z-z0)n+n=0+∞∑ Cn(z-z0)n
Главная часть правая часть
Если хотя бы один из рядов расход, то и ряд Лорана расх.
Главн. и прав.расход, если p< (z-z0)<R
Ряд Лорана сходится в (.)z, если в этой (.) сход оба ряда.
Опр: 1 по степ 1/z-z0, сх-ся (z-z0)>p
2 по степ 1/z-z0, сх-ся(z-z0)<R
Теорема о разлан-ой в кольце ф-ции в ряд Лорана
Если F(z) аналитична в кольце Kr<(z-z0)<R, то она в этом кольце единств образом разлагается в ряд Лорана
F(z)=n=-∞+∞∑ Cn(z-z0)n, z0- центр кольца и Cn= 1/2Пiγ∫ f(ξ)dξ/(ξ-z0)n+1
γ – люб. замкн. контур в кольце K, окружающ (.)z0
Замечание: rи Rопр из расстояния от центра z0до ближ особ (.)-ек
30. Изолированные особые (.) однозначного характера( определения, классифик, примеры) и связь с разложением в ряд Лорана в окруж-ти (.)-ки
Опр: (.)z назыв особой (.)-ой ф-цииf(z), если в ней нарушается аналитичность ф-ций ( fне опр в z)
Опр: Особ (.) изолир, если существует окрестность (.)z0 , в которой нет других особ (.)-ек
Опр: Изолир особ (.) наз-ся
Устранимой, если существует конечнLimz>z0f(z)
Полюсомf(z), еслиLimz>z0f(z)=∞
Существ-ой особ (.), если не существует Limz>z0f(z)