Приложения:

1)масса кривой. L-мат-ая кривая с плотностью M=

2)статистические моментвотн-но оси:

3) коорд.центра тяж.: ;

4) момент инерции:

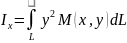
+ –отн.нач.коор-т

13Криволинейные интегралы 2ого рода. Определение. Свойства. Теорема о вычислении с помощью определённого интеграла и теорема о связи криволинейных интегралов 1ого и 2ого рода.

Определение:Векторным полем определён в области , называется ,P,Q,R определены в

(P,Q,R).

Разобьём на n частей

,

, ,

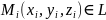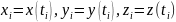
Определение : Интегральной суммой

Определение : Число

Если

Интегралом второго рода от векторного поля

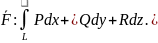
Свойства : 1) =-

2) Свойство аддитивности :

Определение :Пусть контур L замкнута. Если область Д ограниченная контуром L, при обходе по L остаётся слева, то направление обхода положительное, в обратном случае – отрицательное .

Если L– замкнута , то криволинейный интеграл второго рода :

Теорема 1 ( о вычислении интеграла второго рода с помощью определённого интеграла) L- гладкая или кусочно-гладкая кривая : ,

(P,Q,R). Непрерывно (или кусочно-непрерывна ) в некоторой области :

Теорема 2 Связь криволинейного интеграла второго рода с криволинейным интегралом первого рода L- гладкая или кусочно-гладкая кривая : ,

(P,Q,R). Непрерывно (или кусочно-непрерывна ) на L .

Доказательство : Запишем интеграл в правой части уравнения (1) с помощью определённого интеграла

Касательный Вектор L .

)

=

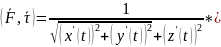Приложения: 1) работа 2)циркуляция векторного поля вдоль L-замкнутая.

14 Потенциальные векторные поля. Потенциальность поля и эквивалентные утверждения о криволинейных интегралах второго рода.

Определение : Пусть область называется потенциальным в если 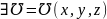такая, что

: Векторное поле

А) = 0,

Б) зависит только от концов А и B и не зависит от кривой соединяющей эти точки .

Доказательство : из А) следует Б) . точки А и B - фиксированные : есть 2 пути из А в В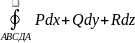 = 0

Из Б) следует А). Пусть интеграл не зависит от пути , только от концов

= 0

Соединяет ; L = АВСДА

Теорема : Пусть потенциально в .

А) не зависит от пути а только от концов ( криволинейный интеграл второго рода)

Б) Пусть криволинейный интеграл второго рода не зависит от пути . А-фиксированная В-переменная.

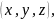; А-фиксированная, В C

U

U .

ВС: , , 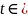dy=0, dz=0

Так как P непрерывна

Аналогично и для других частных производных.

Замечание: Если потенциально и непрерывно дифференцируемо в , то ; ,

.

15.Площадь поверхности:определение,вычисление с помощью двойного интеграла (для пар-кого и явного задания)

Опр.:П-тьпов-ть интегралаквадрируемая,разобъем её конеч. числом глад. кривых на пов-тиS_i Im (S_i),m-площадь

На S_iвыберем (.) M_i^k

Пусть f(x,y,z) определена на интеграле.

T. (о связи пов-го интеграла первого рода с двойным интегралом)

Пусть интеграл-глад.пов-ть =[ _u, _v]≠0

S_i ,(u,v) R² и f непрерывна на S ∃ и = dudv)dS

След.Еслипов-ть интеграла задана явнв,т.е. S:z=z(x,y) (x,y) Д⊂R²

z(x,y) непр-но диф_ма и F(x,y) непр-на на S,то ∃ и =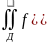 dxdy

16.Повторные интегралы 1-го рода .Определение ,свойства и вычисление с помощью двойного интеграла.

Пусть Sквадрируема и разбита на конечноечисло гладких кривых S=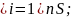

свойства повторного интеграла первого рода

1) =m(S) 2) = α

3)свойство аддитивности 4)свойство непрерывности на S и f(x,y,z)≥0

S=S₁ US₂ (x,y,z) S

+ ≥0

5)f и gнепрерывны f≤g в ∀ (,) S^l,то

6)Если fинтегрируема по s,то интегр. по S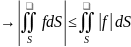

7)теорема о среднем:f-непрерывна ,S-компакт(измерим, гладкий),то ∃ S :

Физические приложения повторного интеграла 1-го рода

1.масса M= dS 2,координаты центра тяжести x_c= dSy_c=… z_c=…

3.момент инерции

I_yz= dS

I_ox= dS

I_o= dS

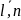Опр.: Интегральной суммой 𝞼_Tпо функции f,разбиению T ,i= ,называется 𝞼_T(f)= )m(S_i)

Опр:Число I называется пределом интегрирования сумм 𝞼_T(f)= )m(S_i),при (T) 0,пишут =I

Если ∀ɛ 0 ∃ = (E) 0:∀T ∀

M_i^* S_i E

Если I ∃,то он называется поверхностным интегралом 1-го рода от f по поверхности S и обозначается или ,функция а называется интегрируемой по пов-ти.

17.Ориентация поверхности .Повторные интегралы 2-го рода и их свойства. вычисление с помощью двойного интеграла.

S-задана и ограничена в имеет 2 стороны поверхности: внутреннюю и внешнюю

Определение : Пусть S,на которой может быть задано векторное поле нормалей,непрерывное на оси поверхности S , называется двухсторонней поверхностью.

и – нормали, = – верт. поле нормалей

Пр.двухст-ей пов-ти:сфера,,элипсойд,гиперболойд

Пр-рыодн-ей пов-ти:лист мебиуса,бутылка Клейна.

Опр.: Двухсторонние пов-тиназ-сяориентируемыми,односторонние-неориентируемыми

Выбор сторон двухст-ей пов-тиназ-ют ориентацией.

1)Если пов-ти заданы пар-ки,то = – одна ориентация,- = вторая ориентация

2)Если S задана явно S:z=z(x,y)

=(- ,- ,1) = – острый

=(- ,- ,-1) = -тупой

= – единич. вектор нормали

П-тьS-огранич. и двухст-яя,S-кусочно глад. пов-ть (или гладкая)

Выберем одну из сторон пов-тиS,определяемую полем нормалей

=(cos , cos ), ⊥S, =1, углы с OX,OY,OZ

Пусть на S задано непрерыввект. поле 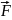=(P,Q,R)

Опр.:Пов-ны интегралом 1-го рода от ф-ийPcosα,Qcos ,Rcos наз-ся поверхностью 2-го рода от ф-ийP,Q,Rсоотв-но и обозначают I₁= ; I₂= ;I₃=

Общим пов-ым интегралом 2-го рода от вект. поля =(P,Q,R) повсейпов-тиSназ-сяпов-ый интегральная 1 рода от скалярного произведения на

I= + + = dS

св-ва интеграла 2-ого рода: 1)при изменении напр-иянормали,тоинтегрируемая меняет знак.

2)св-во лин-ти

3)св-во аддитивности

Поверхн. интегральная 2-го рода наз-ся потоком векторного поля через пов-тьS в направлении нормали к пов-тиS

Если пов-тьзамкнута,то поток через пов-тьS в напр-ии П= dS

Вычисление потоков :

=(P,Q,R) П= dS

= П= dS = = dS= dxdy = dxdy

S:z=z(x,y),(x,y) Д⊂xoy = -острый =(-Z_x^l,-z_y^l)

Добавить к ориентации в начале.

Опр.: ориентация пов-тиS полей нормалей согласовано с + ориентацией простых контуров Г S,если для наблюдателя с выбранной стороны пов-ти,т.е.принапр-ии нормали от ног к голове,при обходе контура Г в положит напр-ие(область слева) ограниченная часть S остается слева.

Опр.: пов-тьS₁ и S₂ склеиваются по кривой ориентация пов-ти S₁ и S₂ согласована,если каждая из них порождает на крив. противоположные ориентации.

18.Ф-ла Грина и ее сл-ие(вычисление пл-ди)Условие потенциальности плоских векторных полей.

(Т-ма) п-ть дано плосское век-ное поле =(P,Q) непр-но диф-мое в =D∪dD ,причем D-огранич. Измерим. мн-во с кусочно-гладкой ф-ией ⇒ – ф-ла Грина