22.Поток поля, дивергенция, соленоидальные поля.З-н сохр-ия интен-ности вект-ной трубки.
Поток
=
Дивергенцией непр-но диф-го поля наз-ся скалярное поле (ф-ия): div =F= + + -сумма частных пр-ных
П≠0⇒divF≠0
divF=0
на Ω`,m(
Опр.: Вект-ное поле наз-ся соленоидальным, если divF≡0( )
Опр.: обл-ть Ω⊂ наз-ся объемно-односвязной, если ∀ замкн-ой пов-ти S⊂Ω и S=dΩ`⇒Ω`целиком⊂Ω
Пр.: шар, паралл-пед-оъемно односвязн.
Соленоид-ое поле в объемно односв-ой обл. обладает св-ом: поток через ∀ замкнут. Пов-ть S⊂Ω равен нулю (след. (Т) Остроградского)
Соленоидальный-т.е. трубчатый
З-н сохран-ия интенс-ти вект-ной трубки
Опр.:Вект-ыми линиями наз-ся кривые в пр-ве в ∀ т-чек кот-ых кас-ый в-р || век-му полю (M)
L:r=r(t)
=
={
,
,
}||
=(P,Q,R)
-кас.век-ор
Ур-ие
век-ой линии в век-ом поле
:
=
=
Опр.: Вект-ой трубкой вект-го поля наз-ся обл-ть в пр-ве, огранич. Век-ыми линиями(бок-ая пов-ть) и 2-мя плоск перпендик-ми вект. лин-ми
Утв.: В соленоидальном поле поток поля через сечение вект. трубки имеет одно и то же знач-ие
=
=0
=
=0
23.Производная ф-циикомплек-гопеременного. Теор о дифференцируемости ф-ии комплексного переменного, условия Коши-Римана. Аналитичность ф-иикомплексного переменного в точке и в области
Опр: F(z) имеет предел А при z→z0 (limF(z)=A),если любое ε>0 существует б=б(ε)>0 любое z:0<(z-z0)<б⇒ (f(z)-A)<ε
Опр: z, z+∆z є Д, W=F(z) определена в Д
∆f=F(z+∆z)-f(z) – прирощ ф-ии
Если любой конеч предел lim ∆f/∆z ,то этот limназ-ся производной ф-ииf в точке z,обозначают f`(z),т.еf`(z)=lim∆F/∆z
Теорема: Критерий диф-сти в точке
Для того чтобы f(z)=u(x,y)+iv(x,y) была диф-ма в точке z0=x0+iy0 Н и Д чтобы: 1) u(x,y) и v(x,y) были диф-мы в точке (x0,y0)
2)
выполнены условия Коши-Риманна в
(x0,y0):
в (x0,y0)
Если f(z) диф-ма в точке z0 ,то f`z можно вычислить по ф-леF`(z)=u`x+iv`x=v`y-iv`y
Пр: w=(x+2y)+i(2x+y)
диф-мы
в любой точке пл-ти → усл К-Р :u`x=1≡v`y=1
→ не выполнен u`y=2≠-v`x=-2
⇒
фу-ия не имеет f`
Аналитичность ф-ии
Опр: f(z) аналитическая в точке z0, если она имеет производную в любой точке некой окр-ти точки z0
Опр:f(z) называется аналитической в обл. Д если она аналитична в любой точке
Опр: точки плоскости в которых однозначна ф-иякомпл-ых переменных аналитична,точки,в которых нарушается аналитичнсоть ф-ии называются особыми
Утв: Сумма произв-ия и частное 2ух аналитич. Ф-ийявл-сяаналитич. Ф-ей
24.Гармонические ф-ии, сопряженные гармонические ф-ии. З-ча восстановления аналитич ф-ии по известной действит.(мнимой) части.
Опр: U(x,y) назы-ся гармонической в Д, если они имеет непрерывные 2-ые частные производные U``xx+U``yy≡0 в Д
Если f(z)аналитична в Д, то она и гармонична в Д,тоf(z) имеет в Д произв. Любого порядка.
Опр: Гарм-ая ф-ияv(x,y) наз-ся сопряженной гармонич. Ф-ии в Д, если в любой точке є Д выполнены усл К-Р.:
З-ча о восст. Аналитич ф-ии по задан. Действ. Или мномой части
Утв1:Любая гармонич. Ф-ия в Д,Д-односвязная ,может явл-сядействит. Или мнимой частью неп-ой анатической фу-ии
Утв2: Аналитич. Ф-иявоссст-ся по своей действи. Или мнимой части однозначно с точностью до постоянной,если ф-иягармонч-ая
П-тьU(x,y) –действит. Часть
U-гармоническая f- аналитич.
f=U+iv
1
способ: dv=v`xdx+v`ydy=-v`ydx+u`xdy⇒v=
=
ydx+u`xdy
2
способ:
⇒v(x,y)=
xdy+
φ(x)⇒dv/dx=v`x
φ`(x)=…= φ(x)
φ(x)=
φ(x)dx+C
v(x,y)=
`xdy+
+
C
25.Интеграл от ф-иикомпл-го переменного: определение,связь с кривыми интегралами,св-ва,примеры.Тоерема Коши для односвязной и многосв-ой областей
Опр:
L-кусочно-глад.
На R,
разбиваем L
на конеч. Число кусков L=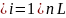
L-измеримы
⇒
существует т (Li)
П-ть на L зад-на непрерывно ф-ми f(z)єC на любом Li выберем точку MiєLi
бt=
(Mi)m(li)
max m(li)→0
Опр:
Число
I наз-сяпределом
суммбtпри
max m(Li)→0,
еслилюбомэпсилон>0
существуетб=б(эпсилон)>0
любогоразбиения
{li},
max m(li)<билюбойвыборки
{Mi}⇒
l бt-I
l <эпсилон
Если
существует I
то I=
(x,y)+iv(x,y))(dx+idy)
=
-
vdy
+ i
+vdx
Св-ва такие же как у крив интеграла 2 рода
Тоер:
Если L
задана пар-киL
:z
=z(x)
,tє(α,ß)
, z(x)=
x(t)+y(y)
, fнепрер-на
на L⇒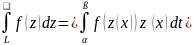
Теор2:
f(z)
аналитична в Д и f(z)
неперывна в Д=ДuαД⇒
Теор3: Коши для многосв-ой области
П-ть граница мн-ой огранич обл. Д состоит из внеш. Контура замкнутого кусочно-глад. ɣ0 пересекающиеся глад-ыхɣ1…ɣn(внутри ɣ0)
f(z)
аналитична в Д и неперывна в Д=Дuɣ0uɣ1…uɣn⇒
=
+
=0
причём контуры ɣ0,ɣ1…ɣn
обходятся в + направлении
След: П-тьf(z) аналитична в Д,то не меня-ся при неперывнойдиф-ии контура, соед-их А и В
Теор: Коши для односв. Обл (сначало эту Тперд Т1)
П-тьf(z)
аналитична в одн-ой обл Д, ɣ
- любое замкнут. Крив-ая ,ɣєД⇒
=0
Опр: Д∈R2 односвязная если любое замкн. єД , ограничД`,целиком лежит в Д