След: (Выч-ие пл-ей с помощью крив-ых инт-лов)
Положим
в ф-ле Грина
или
m(D)=
или
-
или
m(D)=1/2
(Т-ма)Для
того, чтобы непр-но диф-ое вект. Поле
=(P,Q)
было в обл D,
необх-мо, а в случ. Односвязной обл-ти
Dи
дост-но, чтобы в Dвыполнялось
=
Д-во:
необх-ть Ω⊂
-потенциально,
т.е. ∃
U:
∇U=
⇒
=
в
D
Достат-ть:
– непр-но диф-ма в D
=
в D,
В-односвязная
=
=0
-
Ф-ла Грина.
⇔
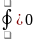-потенциально
∀ L замкну. L⊂DD`:dD`=L ; D-односвяз.⇒D`⊂D
19.Дивергенция.Ф-ла Остроградского и ее усл-ия
Опр:
дивергенцией
непр-но диф-го поля
наз-ся
скалярное поле (ф-ия): div
=F=
+
+
-сумма
частных пр-ных
(Т-ма)
Остроградского Гауса Ω⊂
;
Ω-огранич.
Измер с кусочно-глад. Границей S=dΩ,
ориент-на
внеш-ми полем нормалей
|
|=1
и
непр-но
диф-ма в
=Ω∪dΩ⇒
–ф-ла
Острог-го
След:V=1/3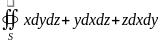
Д-во:
P=x,
Q=y,
R=z,
применим ф-лу Острогр-го
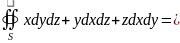
dxdydz
= 3
=3V
20.Ротор. Ф-ла Стокса. Усл-ие. Потенциальности век-ых полей в пр-ве.
Опр:
Ротором непр-го диф-го вект-го поля
=(P,Q,R)
наз-ся век-ое поле rot
=
=(
-
,
-
+
,
-
)
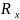(Т-ма)Стокса: =(P,Q,R)- непр-но диф-ое поле в ) S-кусоч-глад., огранич.; S⊂ , L-глад. Кривая; L-граница S, L=dS
=
-
ф-ла Стокса.
Напр-ие движ-ия по контуру L согласовано с напр-ием пов-ти S
Y=
=
)dl=
=
–
Ф-ла Стокса
-еденич
век-р касат. к L
с напр-ием движ. по L
Усл потенц-ии вект. Поля в
Опр.Тело Ω⊂ наз-ся односвязной(поверхн-но односв-ой или лин-но односв-ой если ∀ замкн. Контура L⊂Ω∃ пов-ть S: dS=lи S⊂Ω
Пр.: шар, пр-во с уд-ой т-кой (прямой)
(Т-ма)
Для того чтобы непр-но диф-ое вект-ое
поле
={R,Q,R}
было пот-но необх-мо, а в случ. Поверхн-но
односвяз. Ω и достаточно, чтобы
=
,
+
,
+
в
∀т-ке Ω
и rot
в
Ω
+Rdz=0 ∀Lзамкн. ⊂Ω
такие, что rot
в
Ω
+Rdz= =0,т.к. Ω- пов-но односвяз-ая, то для L∃S:dS=L, S⊂Ω
21.Эл-ты теории поля: оператор ∇, пр-ла д-ия с ним, запись изв-ных опер-ций над полями с помощью ∇.
Скалярное поле =(P,Q,R)
Операции
над полем: 1)
U-век-ное
поле
=
↑↑
|
|=1⇒
=(cosα,cosβ,cosγ)
3)div = + +
4)rot
-вект-ое
поле
Опр:Оператор
Гамильтона(Набла)-Это векторный
опер-р(обозн ∇)
и равный: ∇=
+
=
=(
)
Операции с помощью ∇:
1)∇U=
+
+
=
U
2)
= (∇U,
)
3)div
=(
=
+
+
4)rot
Св-ва оператора Набла:
1)Если
∇
действ-т
,
то выполняется св-во линейн-ти
Пр:
∇(
=
(∇,
=
)
2)Если ∇ действует на произв-ие неск-их ф-иц(скаляр или вект.),то сначала
А) рез-т аналогичен рез-ту диф-ия произ-ия в том смысле что ∇ дей-ет послед-но на каждый сомножитель, а остальные сомн-тели с-мы функциональны и рез-ты складывают
∇(FδH)=∇(
δH)+∇(F
H)+∇(Fδ
)
Б)Преобразуем
слаг-ые в прав. Ч-ти по правилам век-ой
алгебры так,чтобы ∇ стал перед
сомножителем, который
В) выполняем диф-ие ∇ и упрощаем получ. выражение.
Пр.1:
div[
Д-во:div[
=(∇,[
)=(∇,[
)+(∇,[
)
(
∇,[
)=
([∇
)=(rot
=(
,rot
)
Аналогично (∇,[ )=( ,rot )
Пр.2:
rot(U,
)=[∇,U
]=[∇,
,
]+[∇,U,
]=[
∇
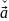]+U[∇,
]=[gradU,
]