
- •7. Преобразование Фурье (прямое, обратное, синус- и косинус-преобразование).
- •9.Двойные интегралы.Сведения двойного инт-лак повторному по прямоуг-ку и элемент обл-сти.Сведения тройного инт-ла.
- •Прилож.Крат.Интегрлов:
- •Приложения:
- •14 Потенциальные векторные поля. Потенциальность поля и эквивалентные утверждения о криволинейных интегралах второго рода.
- •След: (Выч-ие пл-ей с помощью крив-ых инт-лов)
- •19.Дивергенция.Ф-ла Остроградского и ее усл-ия
- •20.Ротор. Ф-ла Стокса. Усл-ие. Потенциальности век-ых полей в пр-ве.
- •22.Поток поля, дивергенция, соленоидальные поля.З-н сохр-ия интен-ности вект-ной трубки.
- •24.Гармонические ф-ии, сопряженные гармонические ф-ии. З-ча восстановления аналитич ф-ии по известной действит.(мнимой) части.
- •26. Первообразная функции и неопределёный интеграл. Тоерема о сущ-нии первообразной для аналитич. Ф-ии. Ф-ла Ньютона-Лейбница
- •Теорема о разложении аналит. Ф-ции в ряд Тейлора
- •Классификация с помощью рядов Лорана.
1. Собственные интегралы зависящие от параметра. Теорема о непрерывности, дифференцируемости и интергрируемости. Примеры.
F(y)=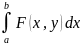 , y∈[c,d]
, x∈[a,b]
– интеграл, зависяший от параметра.
, y∈[c,d]
, x∈[a,b]
– интеграл, зависяший от параметра.
Общ.
случ: F(y)= ,
φ(x),ψ(x)
непрерывны на мн-ве Y.
x∈[φ(x),ψ(x)],
y∈[c,d],
y∈Y.
,
φ(x),ψ(x)
непрерывны на мн-ве Y.
x∈[φ(x),ψ(x)],
y∈[c,d],
y∈Y.
 a
a
с

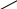


d
φ(x) ψ(x)
1. Непрерывность интеграла.
Теорема. Если F(x,y) непрерывна на b a={(x,y), x∈[a,b], y∈[c,d]}, то F(y)= нер-на на [c,d].
Док-во:
f(x,y) непрерывна на заскнут. мн-ах a → она
равн-но непрерывна Ɐε>0 ∃
δ>0: |F(x,y)-F(x',y')|<ε, если |x-x’|<δ’→
(y-y’)<δ
→ |F(y)-F(y’)|=
-
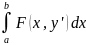 ≤
≤
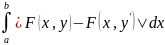 < ε(b-a),
т.е. F(y)
– непр-на.
< ε(b-a),
т.е. F(y)
– непр-на.
2. Интегриров под знаком интеграла.
Теорема.
Если ф-ия F(x,y) определена и непрерывна
в П (прямоугольник) А={(x,y),
x∈[a,b],
y∈[c,d]},
то
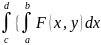 }dy=
}dy=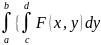 }dx.
}dx.
Пример.
F(x)=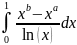 ;
подинт-ая ф-ия: φ(x)=
;
подинт-ая ф-ия: φ(x)= =
= →
F(x,y)=
→
F(x,y)=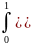 )dx=
)dx=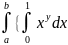 }dy=
}dy= =
=
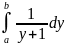 =ln(y+1)
=ln(y+1)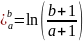
3. Диф-ость по пар-ру.
Теорема.
П-ть F(x,y)
и Fy’(x,y)
непрерывны в П={(x,y),
x∈[a,b],
y∈[c,d]},
то F(x,y)
диф-ма на [a,b] и Fy’(y)=

Теорема.
(общий случай). П-ть ф-ия F(x,y),
 непрерывны в Ω={(x,y):
x∈[φ(x),
ψ(x)],
y∈[c,d]}
и φ(x),
ψ(x)-
непрерывно диф-мы на [c,d]
→
F(y)=
непрерывны в Ω={(x,y):
x∈[φ(x),
ψ(x)],
y∈[c,d]}
и φ(x),
ψ(x)-
непрерывно диф-мы на [c,d]
→
F(y)=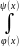 =
=
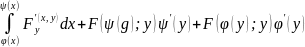
Пр:
F(y)=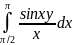
Fy’
(y)= y'dx=
y'dx= dx=
dx=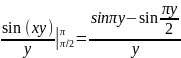
Пр:
F(y)=
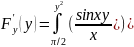 y’dx+
y’dx+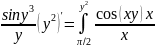 dx+
dx+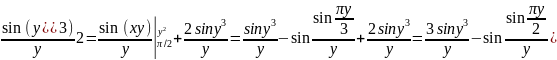 .
.
2. Несобственные интеграллы от парам-ра. Равномерная скорость. Признаки равной сходимости. Примеры.
F(y)= y∈[c,d] либо y∈Y.
1-го рода: b= ±∞ 2-го рода: в F(x,y)→∞ x→∞.
Опр.
Несоб. Интеграл сх-ся рав-но на Y , если
Ɐε>0 ∃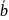 <
(ε):
Ɐη∈[
,b)
и Ɐy∈Y→|
<
(ε):
Ɐη∈[
,b)
и Ɐy∈Y→|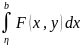 |<ε
|<ε
Признаки: 1 признак Вейерштрасса.
Теорема. П-ть ф-ия F(x,y) непрерывна на [a,b) и F(y)= , y∈Y, сх-ся для y∈Y, если ∃ g(x):
1)|F(x,y)|≤g(x), Ɐx∈[a,b),Ɐ y∈Y
2) -
сх-ся → F(y)=
сх-ся рав-но на Y.
-
сх-ся → F(y)=
сх-ся рав-но на Y.
Пр:
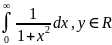 1.|F(x,y)|≤
1.|F(x,y)|≤ ≤
≤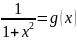
2.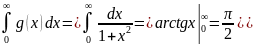 →F(y)
c-cя
равн-но.
→F(y)
c-cя
равн-но.
2 приз-к Коши равн-ой сх-ти.
П-ть
F(y)=
y∈Y
F-непр-на,
x∈[a,b),
y∈Y,
F(y)-с-ся
на Y,
F(y)
с-ся равном-но на Y
тогда и только тогда, когда Ɐε>0,
∃
=
(ε):
Ɐη1,η2≤[
,b)
) и Ɐy∈Y
→
| <ε
<ε
След:
(отрицание крит. Коши) F(y)
cх-ся
равн-но если ∃ε0>0:Ɐ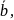 ∃η1,η2
∃η1,η2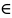 [
,b)
и ∃y0∈Y→|
[
,b)
и ∃y0∈Y→|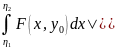 ≥ε0
≥ε0
3-й признак Дирихле:
F(y)=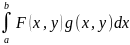 ,
y∈Y(1);
1) |
,
y∈Y(1);
1) |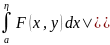 <C,
Ɐη∈[a,b),
т.е … равн-но ограничена. 2)g(x,y) монотонна
по x Ɐ
y∈Y
и
g(x,y)
<C,
Ɐη∈[a,b),
т.е … равн-но ограничена. 2)g(x,y) монотонна
по x Ɐ
y∈Y
и
g(x,y) (равн-но
стремится к 0)→(1) сх-ся рав-но на Y.
(равн-но
стремится к 0)→(1) сх-ся рав-но на Y.
4) Признак Абеля.
; 1) - сх-ся равн-но, 2)g(x,y) монотонна по x Ɐ y∈Y и g(x,y) равн-но ограничена: ∃M: |g(x,y)|≤M, Ɐx∈[a,b), Ɐy∈Y → (1) сх-ся равн-но на Y.
Пр:
F= ,
y≥0
,
y≥0
1.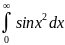 =
=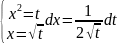 =
=
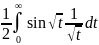 – сходится по призн Дирихле, т.к.
– сходится по призн Дирихле, т.к.
 = -cost
= -cost ≤r,
≤r,
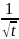 →0
Ɐη:
→0
Ɐη:
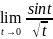 =0
→сх-ся
равн-но по Y.
=0
→сх-ся
равн-но по Y.
3. Несоб. итегр зависящие от параметра. Теорема о непрерывности, диф-ти и интегр-ти. Примеры.
F(y)= y∈[c,d] либо y∈Y.
1-го рода: b= ±∞ 2-го рода: в F(x,y)→∞ x→∞.
b – конечно.
1. Непрер-ть.
П-ть вып-ны усл-ия: 1)F(x,y) непр-на на Q={(x,y), x∈[a,b], y∈[c,d]} 2)F(y)= сх-ся рав-но на
[c,d] → F(y) непрер на [c,d]
Пр:
F(y)= ,
доказать, что сходится непр-но на y≥0;
а) y≠0 y>0
F(y)=
=
,
доказать, что сходится непр-но на y≥0;
а) y≠0 y>0
F(y)=
=

б)
y=0 F(0)=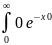 =0.
=0.
F(y)= -
разрыв в (.) 0, но по Т. сх-ся равн-но, то
F(y) должна быть непр-на в Ɐy,
т.е. непр-на в (.) 0→
противоречие→ интегр сходится равн-но.
-
разрыв в (.) 0, но по Т. сх-ся равн-но, то
F(y) должна быть непр-на в Ɐy,
т.е. непр-на в (.) 0→
противоречие→ интегр сходится равн-но.
След.
В усл Т.
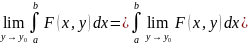
Ɐy0∈[c,d].
2.Перестановка интегр. или интерг под знаком интегр.
Теорема.
1)F(x,y) непрер в Q 2)
сх-ся равн-но на [c,d],
тогда F(y) интегр-ма на [c,d]
и справдливо рав-во:
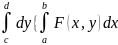 }=
}=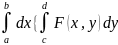 }
}
3. дифф по рапаметру несоб интегр.
Теорема.
1)
F(x,y)
и Fy’(x,y)
непрерывны в П Q={(x,y),
x∈[a,b],
y∈[c,d]}
2)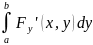 сх-ся рав-но на [c,d].
3)
сх-ся хотя бы при одном y0∈[c,d],
т.е.
сх-ся рав-но на [c,d].
3)
сх-ся хотя бы при одном y0∈[c,d],
т.е.
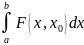 сх-ся →
F(y)=
непрерывно диф-ма на [c,d]
и справедливо след. рав.
сх-ся →
F(y)=
непрерывно диф-ма на [c,d]
и справедливо след. рав.
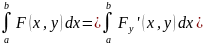 .
.
Порядок вычисления F(y)= , y∈[c,d]
1)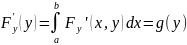
2)F(y)=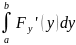 =G(y)+C(1)
=G(y)+C(1)
3)Подобрать y0∈[c,d], так чтобы рассч. исход. интегр. и вычислить по (1) С.
Пр:
F(a)=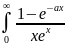 dx,
a>-1
dx,
a>-1
1.F’(a)= dx=
dx=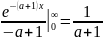
2.F(a)= a>-1
a>-1
3.C-?
П-ть
a=0→F(0)=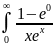 dx=0
в
(1) ln(1+0)+C→C=0.
dx=0
в
(1) ln(1+0)+C→C=0.
Ответ:F(a)=ln(a+1)
4.Эйлеровы интегралы: Гамма ф-ия и ее св-ва.
Опр.: Гамма ф-я Г(х)
– это несобственный инт-л Г(х)=
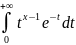 ,
x>0, x – параметр; если х≥1, то несобственный
инт-л только в верхнем пределе; если
хє(0,1), то несобственный инт-л в обоих
пределах.
,
x>0, x – параметр; если х≥1, то несобственный
инт-л только в верхнем пределе; если
хє(0,1), то несобственный инт-л в обоих
пределах.
Г(х)=
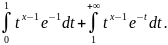
Св-ва: 1) оба инт-ла
правой части равномерно сх-ся равномерно
на Ɐ[a,b]⸦(0,+∞). Док-во: рассмотрим случай
aє(0,1), b>1, xє[a,b]. 1-ый инт-л: tє[0,1] =>
0≤ ≤
≤ ≤
≤ =g(x),
tє(0,1), рассмотрим
=g(x),
tє(0,1), рассмотрим
 – сх-ся по признаку Вейерштрасса. 2-ой
инт-л: t≥1
≤
– сх-ся по признаку Вейерштрасса. 2-ой
инт-л: t≥1
≤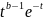 =g(t),
a≤x≤b,
=g(t),
a≤x≤b,
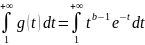 – сх-ся, т.к. g(t)<
– сх-ся, т.к. g(t)<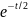 +> 2-ой инт-л сх-ся равномерно по пр-ку
Вейерштрасса.
+> 2-ой инт-л сх-ся равномерно по пр-ку
Вейерштрасса.
2) Г(х) непрерывна на (0,+∞). Док-во: по утв. 1) Г(х) непрерывна на Ɐ[a,b]⸦(0,+∞) => по теореме для несобств. инт-ов Г(х) непрерывна на (0,+∞).
3)Г(х) непрерывно
диф-ма ф-я х при х>0 и Г’(х)=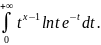
4) Г(х) бесконечно
диф-мая ф-я х при х>0 и Г(n)(х)=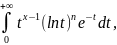 n=0,1,2...
Следствие: F’’(x)>0 Ɐxє(0,+∞).
n=0,1,2...
Следствие: F’’(x)>0 Ɐxє(0,+∞).
5)Ɐx>0: Г(х+1)=хГ(х)
– основное функциональное соотношение.
Док-во: Г(х+1)= |0+∞
+
|0+∞
+
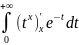 =0+0
+x
=0+0
+x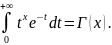
Следствие: Г(n+1)=n!,
Г(1)=1, Г(1/2)=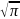 ,
Г(х+1)=хГ(х) Ɐx>0.
,
Г(х+1)=хГ(х) Ɐx>0.
6)Г(х)→+∞ при х→0+.
Док-во: Г(х+1)=хГ(х)
Ɐх>0 →Г(х)=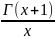 →+∞ при х→0+.
→+∞ при х→0+.
7) Г(х)Г(1-х) =
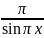 ,
xє(0,1).
,
xє(0,1).
Гр-к Г(х):
Пр.

Г(n+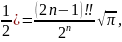 (2n-1)!!=1∙3∙5∙…∙(2n-1).
(2n-1)!!=1∙3∙5∙…∙(2n-1).
5.Эйлеровы
инт-лы: бета-ф-я и ее св-ва. Два вида
записи бета-ф-ии. Вычисление
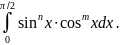
Опр.: бета-ф-я B(x,y)
– инт-л, зависящий от двух переменных
xи
y,
вида
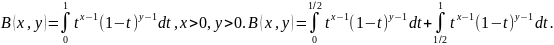 (1-ый инт-л:
(1-ый инт-л:
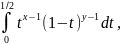 2-ой инт-л:
2-ой инт-л:

Св-ва: 1)B(x,y)
опр-на в x>0,
y>0
=>1-ый и 2-ой инт-лы сх-ся. Док-во: 1-ый
инт-л: t→0+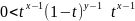 при
t→0+,
при
t→0+,
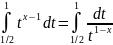 –
сх-ся при х>0. 2-ой инт-л: t→1-
–
сх-ся при х>0. 2-ой инт-л: t→1- при
t→1-,
при
t→1-,
 –сх-ся
при y>0.
–сх-ся
при y>0.
2)B(x,y) непрерывна в x>0, y>0.
3)B(x,y)=B(y,х) Ɐх – симметричная ф-ия
4)(диф-ть) B(x,y) имеет непрерывные частные производные Ɐпорядка по каждой переменной.
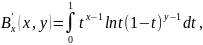
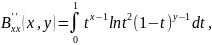

5)
B(x+1, y)=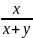 B(x,y),
B(x, y+1)=
B(x,y).
B(x,y),
B(x, y+1)=
B(x,y).
6)
B(x,y)=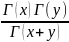 .
.
7)B(x,y)
может быть записана в виде:
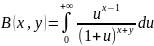 .
.
Пр.:
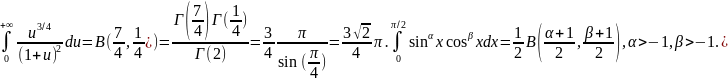
Пр.:
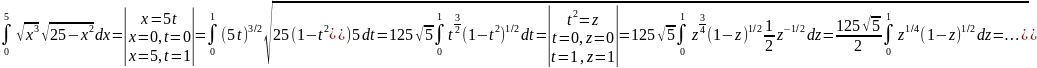
6.Инт-л Фурье. Т. о представимости ф-ии инт-ом Фурье. Пр-ры.
Если
f(x)
задана на Rи
периодична с Т(+cos)=>f(x)=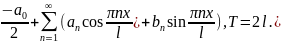
Если
F(x)
непериодична и хорошая, то f(x)=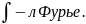
Пусть
f(x)
абс. bнт-ма на числовой прямой, т.е.
 .
Положим: a(y)=
.
Положим: a(y)=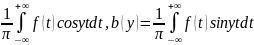 (1)
(1)
Если f(t) инт-ма, то a(y), b(y) непрерывно инт-мы на R.
Несобств. инт-лы в прав. части сх-ся равномерно на всей числовой оси по пр-ку Вейерштрасса.
Ф-ии
f(x) поставим в соответсвие инт-л:
f(x)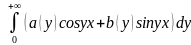 –инт-л
Фурье. (2)
–инт-л
Фурье. (2)
Опр.: инт-л (2) с коэф-ми a(y), b(y), найденными по фрмулам (1), наз-ся инт-ом Фурье, построенным для абсолютно инт-мой ф-и f(x).
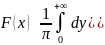 –полный
инт-л Фурье.
–полный
инт-л Фурье.
Т1.
Пусть выполнены усл-я: 1)f(x)
абс. инт-ма на R;
2)х0
– фикс. т-ка и Ǝl>0,
что на [x0-l,
x0+l]ряд
Ф., построенный по ф-и f(x),ортогон.
тригонометр. системе { }
(T=2l),
сх-ся в т-ке x0
(его сумму обозначают S(x0)),
тогда
}
(T=2l),
сх-ся в т-ке x0
(его сумму обозначают S(x0)),
тогда
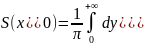 – инт-л Фурье.
– инт-л Фурье.
Т1 позволяет для абс. инт-мой ф-ии получить усл-я представимости ф-и инт-ом Ф. как следствие усл. cх-ти ряда Ф. в т-ке.
Т2. 1) f(x) абс. инт-ма на R; 2) в т-ке х0 для f(x) выполнены усл-я Гёльдера: Ǝc>0, Ǝδ’>0, Ǝαє[0,1]: |f(x0+u) – f(x0+)| ≤cuα
|f(x0+u) – f(x0--)| ≤cuα, uє(0,δ) (f(x0+) = limf(x) при х→x0+)
=>в т-ке х0
ряд Ф. для ф-ии f(x)
и нек-го отр-ка[x0-l,
x0+l],
l>0
сх-ся и
;
если х0–
т-ка непрерывности ф-ии f(x),
то
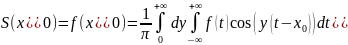 ,
в др. случае
,
в др. случае

Т3. 1) f(x) абс. инт-ма на R; 2) f(x) кусочно-непрерывна на R; 3) f’(x) кусочно-непрерывна, т.е. либо Ǝf’(x0+), либо Ǝf’(x0-) => в т-ах инт-ти f(x) f(x) представима инт-ом Ф.

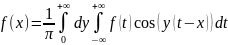 в
т-ке разрыва
в
т-ке разрыва
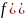
Представление инт-ом Ф. четных и нечетных ф-ий f(x). Выполнены усл-я Т3.
а)
f(x)
четная: a(y)=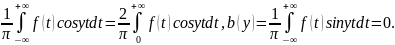 В т-ке непрерывности х f-
четн. =>
В т-ке непрерывности х f-
четн. =>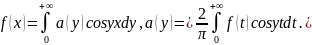
б)
f(x)
– нечетная, то a(y)=0,
b(y)=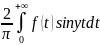 и
в т-ке непрерывности
и
в т-ке непрерывности
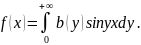
Пр.:
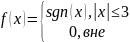 → f(x)
– нечетная →
→ f(x)
– нечетная →
b(y)= подставить
b(y)
в f(x).
подставить
b(y)
в f(x).
Инт-л
Ф. в комплексной форме: если f(x0
инт-ма на числовой оси и удовлетворяет
усл-ям Т3, то в т-ах непрерывности
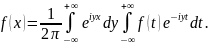
7. Преобразование Фурье (прямое, обратное, синус- и косинус-преобразование).
f(t)
инт-ма на Rи
может принимать конечн. знач.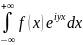 ,
– сх-ся равномерно на Rи
явл-ся непр-ыми фи-и пар-ра уєR.
,
– сх-ся равномерно на Rи
явл-ся непр-ыми фи-и пар-ра уєR.
Опр.: пусть f(x) абс. ф-я на R.
Преобразование
Ф ф-ии f(x)
(F[f]
или
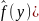 наз-ся
непр., зависящ. от параметра у вида F[f]
=
наз-ся
непр., зависящ. от параметра у вида F[f]
=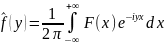 .
Обратным преобразованием Ф наз-ся
инт-л, зав. от пар. у вида F-1[f]=
.
Обратным преобразованием Ф наз-ся
инт-л, зав. от пар. у вида F-1[f]=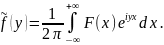
Св-ва:
1) для абс. инт-мой ф-ии
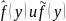 явл-ся огран. и непр. ф-ми на R;
2) если f(x)
абс. инт-ма, кусочно-непрерывна и в Ɐт-ке
оси Ǝ конечная или односторонняя
производная, то преобразование Ф имеет
обратное преобразование ФиF-1[F(f)]=F,
F[F-1[f]]=F,
справедливо во всех т-ках непрерывности
f.
явл-ся огран. и непр. ф-ми на R;
2) если f(x)
абс. инт-ма, кусочно-непрерывна и в Ɐт-ке
оси Ǝ конечная или односторонняя
производная, то преобразование Ф имеет
обратное преобразование ФиF-1[F(f)]=F,
F[F-1[f]]=F,
справедливо во всех т-ках непрерывности
f.
Косинус-преобразование:
если f(x)
абс. инт-ма и четн., то
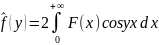 .Синус-преобразование:
Fs[f]=
.Синус-преобразование:
Fs[f]=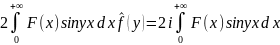 .
.
Если абс. инт-ая ф-ия задана на полуоси (0, +∞), то можно продолжить f на всю ось четным и нечетным образом и написать преобразование Ф.
Пр.:
f(x)=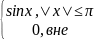 , найти преобразование Ф.
, найти преобразование Ф.
1)f
абс. инт-ма:
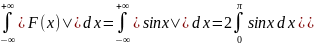
2) f(x) непр. на R
3)f’(x)Ǝ
в всех т-ках, кроме
 a,
ƎF’
(
a)
a,
ƎF’
(
a)
F(x) нечетн.
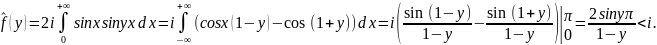
8.Определение о свойства кратных ʃ-ов : разбиения , ʃ-ая сумма , ʃ-ал Римана , св-ва ʃ-ов . Усл-ия ʃ-мости ф-ции . Классы ʃ-ых ф-ций.
Опр:
Ω ᴄ изм-ое
мн-во Совокупность измеримых мн-в { Ωi
} , i=
I,k,
наз-ся разбиением Ω, если:
1)
изм-ое
мн-во Совокупность измеримых мн-в { Ωi
} , i=
I,k,
наз-ся разбиением Ω, если:
1)
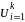 Ωi=Ω2)
Ωi=Ω2)
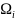 П
П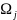 =0,i≠jОпр:
Ω-измер-оемн-во, Т= {
},i=I,k–разбиение
Ωξ={
=0,i≠jОпр:
Ω-измер-оемн-во, Т= {
},i=I,k–разбиение
Ωξ={
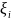 }
– наз-ся выборкой, еслиξ∈
,
i=
I,k
, f(x)
определена наизмер-ом мн-веΩ , Т-разбиение
и ξ-выборка
Выражение вида
}
– наз-ся выборкой, еслиξ∈
,
i=
I,k
, f(x)
определена наизмер-ом мн-веΩ , Т-разбиение
и ξ-выборка
Выражение вида
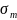 (f)=
(f,ξ)=
(f)=
(f,ξ)=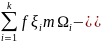 наз-ся
ʃ-ой суммой, построен по f,разбиение
ТВыборка-ξ.
m(
)-мера(объём)
П-тьF-огранич.на
Ω=>ꓱ
наз-ся
ʃ-ой суммой, построен по f,разбиение
ТВыборка-ξ.
m(
)-мера(объём)
П-тьF-огранич.на
Ω=>ꓱ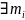 =inFf(x)
=inFf(x)
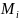 =supf(x)
и определена верх. и нижн. cуммы
Дарбу Sт=Σ
; m(
)
, Iт=Σ
=supf(x)
и определена верх. и нижн. cуммы
Дарбу Sт=Σ
; m(
)
, Iт=Σ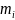 ,m(
)
Опр : Число l-наз-ся
пределом ʃ-ых сумм
,m(
)
Опр : Число l-наз-ся
пределом ʃ-ых сумм
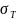 (F,ξ)
при d(T)→0,если
∀ε>0
(F,ξ)
при d(T)→0,если
∀ε>0
 δ=δ(ε)>0
∀Ti
: d(T)<δи
∀ξ=>Iσт(f,ξ)
–II<ε,
пишут lim
(F,ξ)=IОпр:
Диаметром мн-ва-
δ=δ(ε)>0
∀Ti
: d(T)<δи
∀ξ=>Iσт(f,ξ)
–II<ε,
пишут lim
(F,ξ)=IОпр:
Диаметром мн-ва-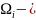 d(Ωi)=supƍ(x,y)
, x
, yϵR^n
; ƍ(x
, y)=
d(Ωi)=supƍ(x,y)
, x
, yϵR^n
; ƍ(x
, y)=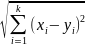 Опр:Если
конеч предел Iинт-ых
сумм
(F,ξ),
при d(T)→0,
то Iназ-ся
ʃ-ом Римана от ф-ииfпо
Ω и обознач-сяI=
Опр:Если
конеч предел Iинт-ых
сумм
(F,ξ),
при d(T)→0,
то Iназ-ся
ʃ-ом Римана от ф-ииfпо
Ω и обознач-сяI=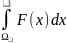 =
= ….ʃF(X1,X2,….,Xn)dx1,dx2,.,dxn-n-ый
ʃ-ал Римана. Опр:
Если
I=
….ʃF(X1,X2,….,Xn)dx1,dx2,.,dxn-n-ый
ʃ-ал Римана. Опр:
Если
I=
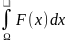 ;
Ωϵ
, то f(x)
наз-сяинтегр-ой на Ω n=2
двойной ʃ-ал: I=ʃʃF(x1,x2)dx1,dx2
или I=ʃʃF(x
, y)dxdyПри
n=1
новое опр. ʃ-ла Римана , в кот. Ω-∀
инт-оемн-во на R=>1)f(x)
инт-ма на [a
, b]
в нов. смысле=>ʃ-ема на [a
, b]
в старом смысле . 2)Если fне
инт-ма на [a,
b]
в стар. смысле , то она не инт-ма в
нов.смысле.Св-вакратн.
ʃ-ла
1)
;
Ωϵ
, то f(x)
наз-сяинтегр-ой на Ω n=2
двойной ʃ-ал: I=ʃʃF(x1,x2)dx1,dx2
или I=ʃʃF(x
, y)dxdyПри
n=1
новое опр. ʃ-ла Римана , в кот. Ω-∀
инт-оемн-во на R=>1)f(x)
инт-ма на [a
, b]
в нов. смысле=>ʃ-ема на [a
, b]
в старом смысле . 2)Если fне
инт-ма на [a,
b]
в стар. смысле , то она не инт-ма в
нов.смысле.Св-вакратн.
ʃ-ла
1)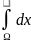 =m(Ω)
2)Если F1,F2-ʃ-мы
на Ω, то αF1+βF2-ин-мы
на Ω а
=m(Ω)
2)Если F1,F2-ʃ-мы
на Ω, то αF1+βF2-ин-мы
на Ω а
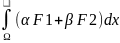 =αʃF1dx+
βʃF2dx
, ∀α,β∈R3)Если
F1,F2
инт-мы на Ω,то f1
=αʃF1dx+
βʃF2dx
, ∀α,β∈R3)Если
F1,F2
инт-мы на Ω,то f1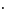 f2
инт-мы на Ω 4)
f2
инт-мы на Ω 4) =
=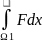 +
+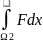 ,
Ω=Ω1∪Ω2 , Ω1,nΩ2≠0
5)Если fинт-ма
на Ω и f(x)≥0
∀x
∈ Ω=>ʃfdx≥0
6)Если f1,f2
инт-мы на Ω и f1(x)≤f2(x)
∀∈Ω , то ʃF1dx≤ʃF2dx
7)Если Fинт-мы
на Ω,то lFIинт-ем
на Ω и справедливо нер-во:
,
Ω=Ω1∪Ω2 , Ω1,nΩ2≠0
5)Если fинт-ма
на Ω и f(x)≥0
∀x
∈ Ω=>ʃfdx≥0
6)Если f1,f2
инт-мы на Ω и f1(x)≤f2(x)
∀∈Ω , то ʃF1dx≤ʃF2dx
7)Если Fинт-мы
на Ω,то lFIинт-ем
на Ω и справедливо нер-во:
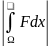 ≤
≤ 8)(Tо
среднем) Если Ω-измерим связный конпакт
и Fнепрер-на
на Ω , то
8)(Tо
среднем) Если Ω-измерим связный конпакт
и Fнепрер-на
на Ω , то
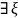 ϵ Ω ; ʃFdx=f(ξ)
·m(Ω)
Опр: Ср-им знач. ʃ-ой ф-ииFна
Ω наз-ся число равное Fср=
ϵ Ω ; ʃFdx=f(ξ)
·m(Ω)
Опр: Ср-им знач. ʃ-ой ф-ииFна
Ω наз-ся число равное Fср=
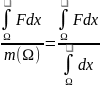
Классы
ʃ-ойф-иив
(T)
Длятогочтобыогранич. наизм-оммн-ве Ω
F(x)
была ʃ-нананёмНиД , чтобы ∀ε>0
∃δ(ε)>0,∀ разбиениеT,d(T)<r=>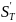 -
-
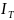 <ε,т.е.
lim
(Sт-Iт)=0
; Ω=∪Ωi
{Ωi}-разбиениеTI)Непрерывныеф-ии
, неизмерим. Ω интегр-минанёмII)Если
ф-ияf(x)огранич.
на Ω и мн-во (.)-ек разрыва имеет жандарову
меру O,
то она ʃ-ма на Ω.Мн-во Ω изм-мо в
,
если оно ограничено и его границы имеют
жандарову меру O
в
Если
мн-во Д с Rизмеримо
и огранич. и F(x)
непр-на (кусочно непр-на), то её график
на мн-ве Д имеет жанд-ву меру Oв
<ε,т.е.
lim
(Sт-Iт)=0
; Ω=∪Ωi
{Ωi}-разбиениеTI)Непрерывныеф-ии
, неизмерим. Ω интегр-минанёмII)Если
ф-ияf(x)огранич.
на Ω и мн-во (.)-ек разрыва имеет жандарову
меру O,
то она ʃ-ма на Ω.Мн-во Ω изм-мо в
,
если оно ограничено и его границы имеют
жандарову меру O
в
Если
мн-во Д с Rизмеримо
и огранич. и F(x)
непр-на (кусочно непр-на), то её график
на мн-ве Д имеет жанд-ву меру Oв

