Уравнения линии конечной длины
Постоянные
и
в
полученных в предыдущей лекции формулах
|
(5) |
;
|
(6) |
определяются на основании граничных условий.
П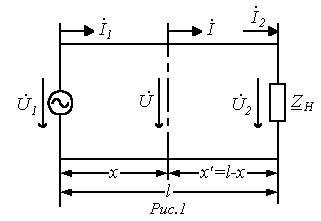
усть
для линии длиной l (см. рис. 1) заданы
напряжение
и
ток
в
начале линии, т.е. при
.
Тогда из (5) и (6) получаем
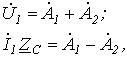
откуда
Подставив найденные выражения и в (5) и (6), получим
|
(7) |
|
(8) |
Уравнения
(7) и (8) позволяют определить ток и
напряжение в любой точке линии по их
известным значениям в начале линии.
Обычно в практических задачах бывают
заданы напряжение
и
ток
в
конце линии. Для выражения напряжения
и тока в линии через эти величины
перепишем уравнения (5) и (6) в виде
|
(9) |
;
|
(10) |
. Обозначив
и
,
из уравнений (9) и (10) при
получим
откуда
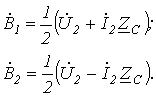
После
подстановки найденных выражений
и
в
(9) и (10) получаем уравнения, позволяющие
определить ток и напряжение по их
значениям в конце линии
|
(11) |
;
|
(12) |
.
Уравнения длинной линии как четырехполюсника
В соответствии с (11) и (12) напряжения и токи в начале и в конце линии связаны между собой соотношениями
;
.
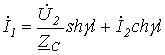Эти
уравнения соответствуют уравнениям
симметричного четырехполюсника,
коэффициенты которого
;
и
;
при этом условие
выполняется.
Указанное означает, что к длинным линиям могут быть применены элементы теории четырехполюсников, и, следовательно, как всякий симметричный четырехполюсник, длинная линия может быть представлена симметричной Т- или П- образной схемами замещения.
Определение параметров длинной линии из опытов холостого хода и короткого замыкания
Как и у четырехполюсников, параметры длинной линии могут быть определены из опытов холостого хода (ХХ) и короткого замыкания (КЗ).
При
ХХ
и
,
откуда входное сопротивление
|
(13) |
. При
КЗ
и
.
Следовательно,
|
(14) |
. На основании (13) и (14)
|
(15) |
и
,
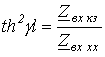откуда
|
(16) |
. Выражения
(15) и (16) на основании данных эксперимента
позволяют определить вторичные параметры
и
линии,
по которым затем могут быть рассчитаны
ее первичные параметры
и
.
Линия без потерь
Линией
без потерь называется линия, у которой
первичные параметры
и
равны
нулю. В этом случае, как было показано
ранее,
и
.
Таким образом,
,
откуда
.
Раскроем
гиперболические функции от комплексного
аргумента
:
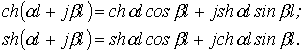
Тогда для линии без потерь, т.е. при , имеют место соотношения:
и
.
Таким образом, уравнения длинной линии в гиперболических функциях от комплексного аргумента для линии без потерь трансформируются в уравнения, записанные с использованием круговых тригонометрических функций от вещественного аргумента:
|
(17) |
;
|
(18) |
. Строго
говоря, линия без потерь (цепь с
распределенными параметрами без потерь)
представляет собой идеализированный
случай. Однако при выполнении
и
,
что имеет место, например, для
высокочастотных цепей, линию можно
считать линией без потерь и, следовательно,
описывать ее уравнениями (17) и (18).
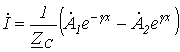
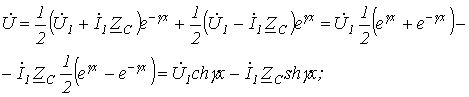
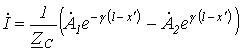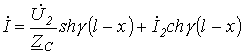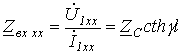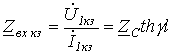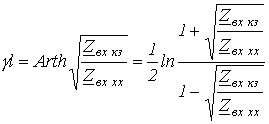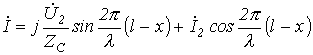