
- •Введение
- •1. Матрицы и действия с матрицами
- •2. Определители
- •3. Обратная матрица. Решение матричных уравнений
- •4. Ранг матрицы
- •5. Системы линейных уравнений. Основные понятия
- •6. Решение линейных систем по формулам Крамера
- •7. Решение систем с помощью обратной матрицы
- •8. Исследование систем линейных уравнений. Метод Гаусса
- •9. Однородные системы
- •10. Собственные значения и собственные векторы матрицы
- •Индивидуальное задание
- •Приложение
- •Литература
9. Однородные системы
Система однородных уравнений всегда совместна. Если ранг матрицы коэффициентов равен числу неизвестных, то система имеет единственное нулевое (тривиальное) решение.
Если ранг матрицы
однородной системы на единицу
меньше числа
неизвестных, то система имеет одну
степень свободы, и ее решение можно
записать через миноры матрицы
.
Для этого в матрице
необходимо оставить
![]() линейно независимых строк, а затем
вычислить миноры, поочередно вычеркивая
столбцы и изменяя знак при каждом
переходе.
линейно независимых строк, а затем
вычислить миноры, поочередно вычеркивая
столбцы и изменяя знак при каждом
переходе.
Так для системы двух линейных однородных уравнений с тремя неизвестными

решение имеет вид
 ,
где
,
где
![]() ,
если хотя бы один из определителей
второго порядка не равен нулю.
,
если хотя бы один из определителей
второго порядка не равен нулю.
►Пример 13. Решить систему

Решение.
Матрица коэффициентов
 ;
;

Минор
 Следовательно, ранг матрицы коэффициентов
равен двум и на единицу меньше числа
неизвестных. Оставив в матрице
две линейно независимых строки
Следовательно, ранг матрицы коэффициентов
равен двум и на единицу меньше числа
неизвестных. Оставив в матрице
две линейно независимых строки
 ,
получаем решение:
,
получаем решение:
 .
.
Ответ:
 .◄
.◄
Упражнения.
Решить системы:
1) 2)
2)
 3)
3)

Ответы: 1) ;
2)
;
2)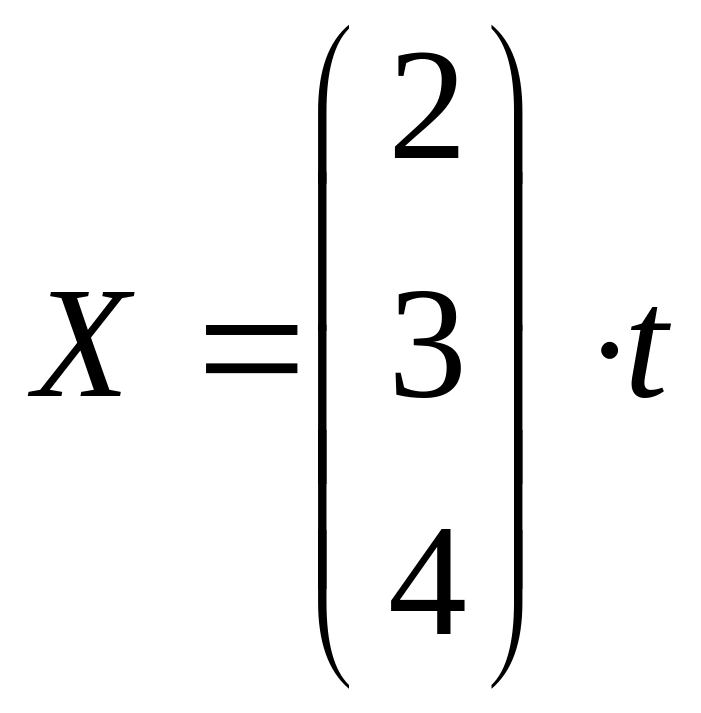 ;
3)
;
3)
 ;
.
;
.
10. Собственные значения и собственные векторы матрицы
Комплексное число
![]() называется собственным
числом
квадратной матрицы
,
если существует ненулевой вектор
(матрица-столбец)
,
такой, что выполнено равенство
называется собственным
числом
квадратной матрицы
,
если существует ненулевой вектор
(матрица-столбец)
,
такой, что выполнено равенство
![]() .
(13)
.
(13)
Вектор называется в этом случае собственным вектором матрицы , соответствующим числу .
Собственный
вектор определяется с точностью до
множителя, т. к. если
удовлетворяет уравнению (13), то и вектор
![]() ,
где t
– любое
число, не равное нулю, тоже удовлетворяет
уравнению (13).
,
где t
– любое
число, не равное нулю, тоже удовлетворяет
уравнению (13).
Матричное уравнение (13) эквивалентно однородной системе
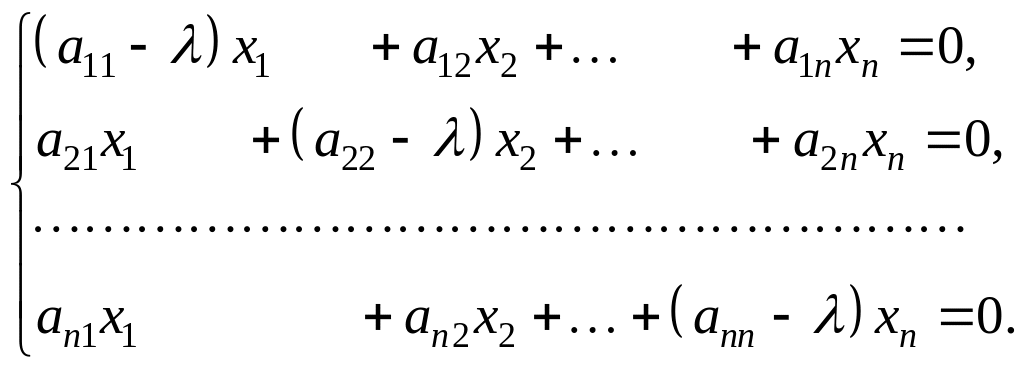 (14)
(14)
Для того чтобы система (14) имела ненулевое решение, необходимо и достаточно, чтобы определитель этой системы был равен нулю:
 (15)
(15)
Уравнение (15) называется характеристическим уравнением для матрицы и представляет собой алгебраическое уравнение - ой степени относительно . Его корни и являются собственными числами матрицы .
Если матрица - диагональная, т.е.
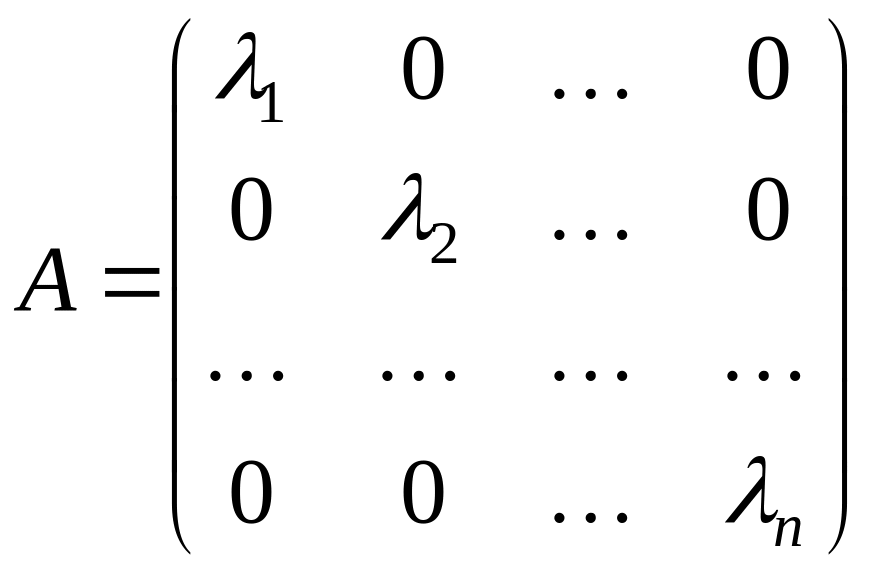 ,
(16)
,
(16)
с разными числами
по диагонали (![]() ),
то собственные числа совпадают с
диагональными элементами матрицы
.
),
то собственные числа совпадают с
диагональными элементами матрицы
.
Как известно из курса алгебры , уравнение (15) имеет, по крайней мере, один корень и, следовательно, у любой матрицы есть хотя бы одно собственное число, а пример с матрицей (16) показывает, что у матрицы размера максимум собственных чисел. Чтобы найти собственные числа, надо решить уравнение (15). Для нахождения собственных векторов решается система (14) при найденных значениях .
►Пример 14. Найти
собственные числа матрицы
 .
.
Решение. Составим характеристическое уравнение и решим его
 .
.
Вычислим определитель:

Уравнение
![]() имеет три действительных корня:
имеет три действительных корня:
![]() ,
которые и являются собственными числами.
◄
,
которые и являются собственными числами.
◄
►Пример 15. Найти собственные векторы для матрицы примера 14.
Решение.
Для того чтобы найти собственный вектор,
соответствующий собственному числу
,
надо решить систему (14), подставив в нее
значение числа
.
Найдем собственный вектор для числа
![]() .
Для этого решим однородную систему
.
Для этого решим однородную систему
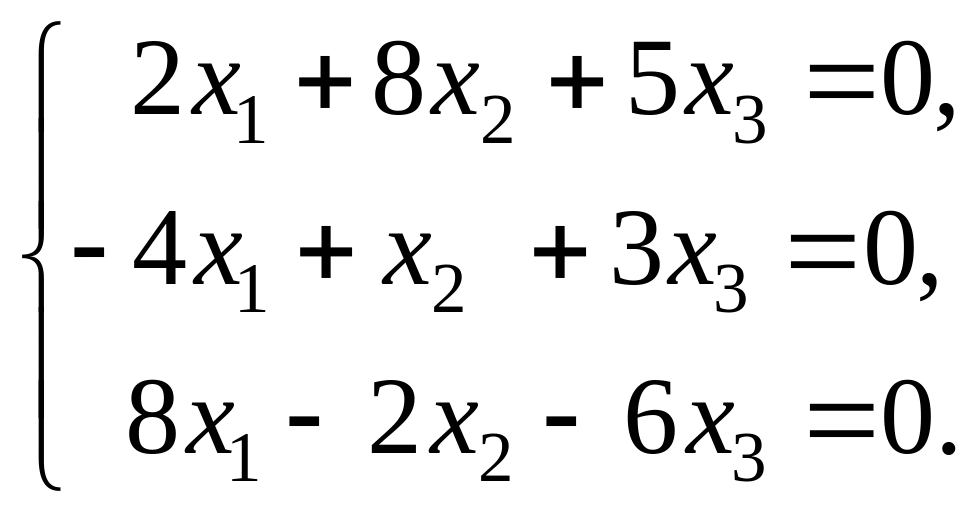
Ранг матрицы этой системы равен двум, на единицу меньше числа неизвестных. Решение (см. пример 13) найдем через миноры матрицы
 :
:

Итак, собственный
вектор имеет вид
 ,
где
,
где
![]() любое число, не равное нулю. Аналогично
находятся два других вектора.
◄
любое число, не равное нулю. Аналогично
находятся два других вектора.
◄
Упражнения.
Найти собственные числа, и для действительных собственных чисел найти собственные векторы матриц:
1) ,
2)
,
2)
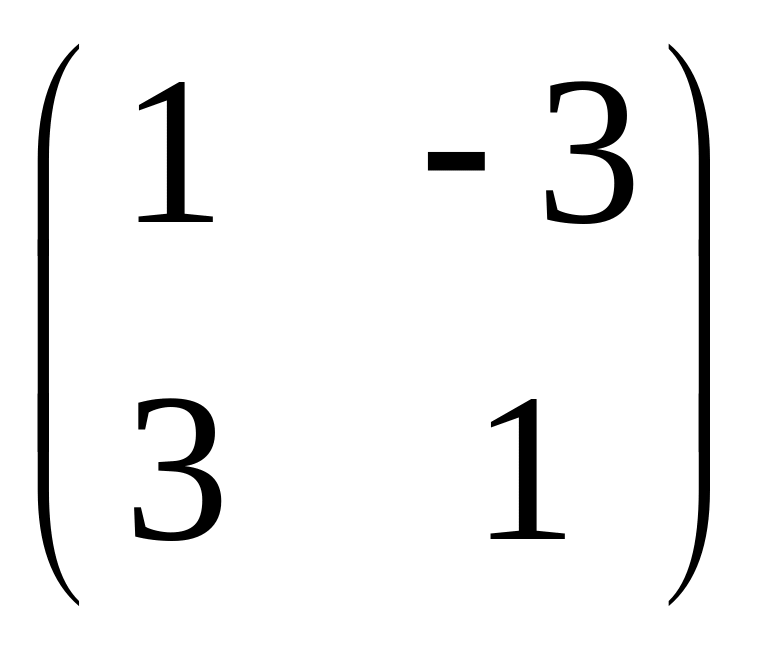 ,
3)
,
3)
 ,
4)
,
4) ,
5)
,
5) ,
6)
,
6) ,
7)
,
7) .
.
Ответы:
 ;
; ;
; ;
; ;
; ;
; ;
; .
.
