2. Определители

Определителем (детерминантом) n-го порядка называется числовая характеристика квадратной матрицы A размера , вычисляемая по определенному правилу (см., например, ). Обозначается определитель одним из следующих символов: .

Определитель первого порядка – определитель для матрицы размера , состоящей из одного числа, – равен самому числу:

.

Для определителей второго и третьего порядков имеем:

; (1)

(2)

При вычислении определителя третьего порядка удобно пользоваться следующей схемой (схема Саррюса):

Рис. 2

Определитель равен алгебраической сумме произведений элементов, соединенных на рисунке одной непрерывной линией. Для определителей порядка выше третьего подобных простых схем не составлено, и для вычисления надо использовать упрощения, основанные на свойствах определителей.

Введем несколько важных понятий.

Минором определителя −го порядка называется определитель, полученный из данного вычеркиванием −ой строки и −го столбца.

В общем случае минором прямоугольной матрицы называется любой определитель, полученный из нее в результате вычеркивания каких-то строк или столбцов. В частности, сам определитель квадратной матрицы тоже является ее минором. Миноры выделены в силу их важности для приложений.

Алгебраическим дополнением к элементу определителя называется выражение

.

Для вычисления определителя −го порядка справедливы рекуррентные формулы через определители ( )−го порядка:

(3)

. (4)

Формулы представляют разложение определителя: (3) − по элементам строки, (4) − по элементам столбца, и, в частности, показывают, что определитель не изменяется при перестановке строк со столбцами, т.е. определители исходной матрицы и транспонированной к ней равны.

Свойства определителей

Так как определитель не меняется при транспонировании матрицы, свойства, приведенные ниже для строк, справедливы и для столбцов.

1. Определитель, имеющий нулевую строку равен нулю.

2. Определитель, у которого две строки равны или пропорциональны, равен нулю.

3. Общий множитель строки можно выносить за знак определителя.

4. Перестановка двух строк определителя изменяет знак определителя.

5. Если строку определителя умножить на постоянное число и прибавить к другой строке, то определитель не изменится.

6. Сумма произведений элементов строки на соответствующие алгебраические дополнения к элементам другой строки равна нулю.

7. Определитель можно представить в виде суммы определителей согласно формуле

.

8. Определитель .

То есть определитель треугольной матрицы равен произведению ее диагональных элементов.

9. Определитель произведения квадратных матриц равен произведению определителей этих матриц: .

►Пример 2. Вычислить определители:

1) , 2) , 3) , 4) , 5) ,

6) , 7) .

Решение.

1) Определитель вычислим по формуле (1)

.

2) Для сравнения определитель вычислим по формулам (2) и (3). По формуле (2): Для вычисления по формуле (3) возьмем вторую строку (выбор строки произволен) и вычислим миноры и алгебраические дополнения к элементам этой строки

.

.

По формуле (3) имеем .

3) В определителе во втором столбце имеется два нуля. Воспользуемся формулой (4) и выберем для разложения второй столбец

.

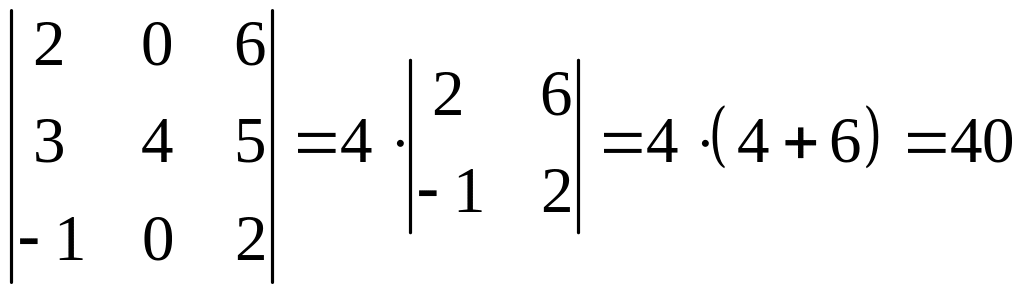4) Первый столбец определителя имеет общий множитель. Вынесем этот множитель за знак определителя

.

5) Имеем определитель треугольной матрицы , следовательно, по свойству (8): .

6) Воспользуемся формулой (3), а определители третьего порядка вычислим по схеме Саррюса:

◄7) Определитель имеет пятый порядок. Разложение по элементам строки (столбца) приводит к пяти определителям четвертого порядка, что в свою очередь дает для каждого из них четыре определителя третьего порядка. Многовато! Воспользуемся пятым свойством определителей. Умножим первую строку на минус единицу и прибавим ее ко второй строке. Затем последовательно первую строку умножим на минус два и прибавим к третьей строке; первую строку умножим на минус три и прибавим к четвертой строке: первую строку умножим на минус четыре и прибавим ее к четвертой строке. Замечаем, что первая строка при наших действиях остается неизменной, поэтому все операции можно сделать за один шаг перехода. Договоримся условно записывать сделанные операции над равенством перехода. Получаем

◄

►Пример 3. Решить уравнение .

Решение. По формуле (1) раскроем определитель, а затем решим уравнение

. ◄

►Пример 4. Найти определитель n-го порядка .

Решение.

Все столбцы, начиная со второго, прибавим к первому столбцу, вынесем общий множитель из вновь полученного первого столбца, а затем первую строку вычтем из всех остальных

◄

Упражнения.

1. Вычислить определители:

а) ; б) ; в) ; г) ; д) ; е) ; ж) ;

з) ; и) ; к) .

Ответы:

а) -12; б) 29; в) 87; г) ; д) 0; е) 48; ж) 160; з) ; и) 394; к) 665.

2. Найти значение , при котором . Ответ: -3.

3. Найти положительное значение , если . Ответ: 2.

4. Доказать:

а) ; б) ;

в) ; г) .

д) .

6. Вычислить определители:

а) ; б) ;

в) ; г) .

Ответы:

а) -1487600; б) -29 400 000; в) ; г) .

7. Найти сумму всех алгебраических дополнений определителя . Ответ: .

8. Известно, что числа 20604, 53227, 25755, 20927, 289 делятся на 17. Не вычисляя определитель , показать, что он тоже делится на 17.