6.3. Кс-грамматики и мп-автоматы.
Контекстно-свободная грамматика (КС-грамматика, бесконтекстная грамматика) — частный случай формальной грамматики (тип 2 по иерархии Хомского), у которой левые части всех продукций являются одиночными нетерминалами. Смысл термина «контекстно-свободная» заключается в том, что возможность применить продукцию к нетерминалу, в отличие от общего случая неограниченной грамматики Хомского, не зависит от контекста этого нетерминала.
Применение
КС-грамматики находят большое применение в информатике. Ими задаётся грамматическая структура большинства языков программирования, структурированных данных и т. д. (см. грамматический анализ)
Для разбора КС-грамматики достаточно автомата со стеком, для разбора не-КС-грамматик может потребоваться полная машина Тьюринга.
Примеры КС-грамматик и соответствующих им КС-языков:
Слово с переворотом
Задаётся формулой
Терминалы: буквы алфавита Σ;
Нетерминал: S;
Продукции:
Начальный нетерминал — S.
Вложенные скобки
Терминалы: '(' и ')';
нетерминал: S;
продукции: S→(S), S→ε;
начальный нетерминал — S.
Этой грамматикой задаётся язык вложенных скобок { (n)n | n≥0 }.
Язык Дика
Арифметическое выражение
Терминалы: '+', '-', '*', '/', '(', ')', 'x'
нетерминалы: <выражение>, <слагаемое>, <множитель>
продукции:
<выражение> → <выражение> + <слагаемое>,
<выражение> → <выражение> - <слагаемое>,
<выражение> → <слагаемое>,
<слагаемое> → <слагаемое> * <множитель>,
<слагаемое> → <слагаемое> / <множитель>,
<слагаемое> → <множитель>,
<множитель> → ( <выражение> ),
<множитель> → x,
начальный нетерминал: <выражение>.
Этой грамматикой задаётся арифметическое выражение, содержащее простейшие арифметические действие над переменной x. Если заменить терминал 'x' на нетерминал <число> из предыдущего примера, то получится грамматика, задающая арифметическое выражение, состоящее из операций сложения, вычитания, умножение и деления над целыми числами.
Язык, который может быть задан КС-грамматикой, называется контекстно-свободным языком или КС-языком.Следует заметить, что по сути КС-грамматика — другая форма БНФ.
МП-автоматы – автоматы с магазинной памятью.
Автомат с магазинной памятью — это конечный автомат, который использует стек для хранения состояний.
Формальное определение
диаграмма автомата с магазинной памятью
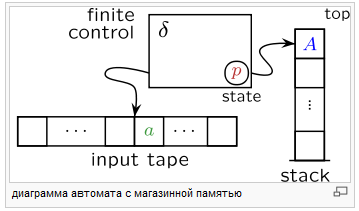
В отличие от конечных автоматов, автомат с магазинной памятью является набором:
где
K — конечное множество состояний автомата
— единственно допустимое начальное состояние автомата
— множество конечных состояний, причём допустимо F=Ø, и F=K
Σ — допустимый входной алфавит, из которого формируются строки, считываемые автоматом
S — алфавит памяти (магазина)
— нулевой символ памяти.
Память работает как стек, то есть для чтения доступен последний записанный в неё элемент. Таким образом, функция перехода является отображением . То есть, по комбинации текущего состояния, входного символа и символа на вершине магазина автомат выбирает следующее состояние и, возможно, символ для записи в магазин. В случае, когда в правой части автоматного правила присутствует , в магазин ничего не добавляется, а элемент с вершины стирается. Если магазин пуст, то срабатывают правила с в левой части.
Автомат с магазинной памятью может распознать любой контекстно-свободный язык.
В чистом виде автоматы с магазинной памятью используются крайне редко. Обычно это модель используется для наглядного представления отличия обычных конечных автоматов от синтаксических грамматик. Реализация автоматов с магазинной памятью отличается от конечных автоматов тем, что текущее состояние автомата сильно зависит от любого предыдущего.
Виды автоматов с магазинной памятью
Существуют детерминированные и недетерминированные автоматы с магазинной памятью.
Для недетерминированных автоматов (в отличие от детерминированных) существует два эквивалентных критерия завершения работы:
пустой магазин
достижение конечного состояния
Детерминированный автомат завершает работу лишь тогда, когда достигает конечного состояния.