
Щерба В.В. Криптографическая защита информации
.pdf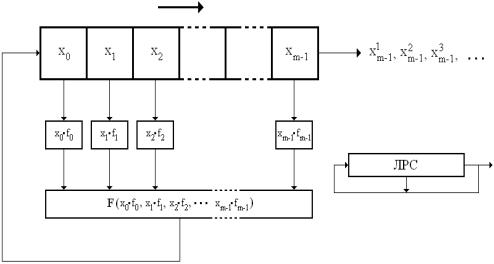
61
учета, рассылки кольцевых перфолент, особенно в условиях военного времени первой мировой войны, стали непреодолимыми.
Известно, что шифр, в котором размер гаммы равен размеру шифруемого сообщения, а каждый ее бит является независимой случайной величиной, обеспечивает абсолютную криптографическую стойкость. Однако обмен пользователями криптографической системы секретными параметрами, размер которых равен объему передаваемых сообщений, нерационален. В связи с этим на практике гамма формируется как псевдослучайная последовательность, полученная на основе относительно короткого криптографического ключа, обмен значениями которого для криптографии выступает традиционной задачей.
Для получения таких последовательностей используются различные датчики псевдослучайных чисел. В настоящее время большинство датчиков псевдослучайных чисел, в том числе реализованных аппаратными или программными продуктами ведущих фирм, построено на основе регистров сдвига с линейными функциями обратной связи или линейных регистрах сдвига (рис. 6.1. Регистр сдвига с обратной связью).
Рис. 6.1. Регистр сдвига с обратной связью
Работа таких регистров осуществляется под управлением так называемого вектора инициализации, представляющего начальное заполнение регистра сдвига. Значение вектора инициализации является криптографическим ключом соответствующего шифра. Одинаковые значения вектора инициализации позволяют формировать на прием-
62
ной и передающей стороне одинаковые псевдослучайные последовательности.
В начале работы в линейный регистр сдвига записывается вектор инициализации: x00, x10, x20, … xm-10. Далее каждый j-ый цикл работы регистра образован двумя тактами. На первом такте текущие значения разрядов регистра умножаются на коэффициенты fi, полученные произведения суммируются. На втором такте выполняется сдвиг содержимого регистра на один разряд вправо. При этом значение старшего разряда xm-1j регистра становится очередным значением гаммы γj, в младший разряд регистра записывается полученное на предыдущем такте значение суммы произведений. Функция F=x0·f0+x1·f1+ … +xm-1·fm-1 называется функцией обратной связи линейного регистра сдвига. При определенных условиях она задает максимальный период гаммы – число ее неповторяющихся значений, не менее чем qn-1, где q – число разрядов регистра, а n – степень многочлена.
Несмотря на то, что линейные регистры сдвига способны формировать управляющие последовательности с большим периодом и хорошими статистическими качествами, структура таких последовательностей достаточно проста. В связи с этим в практической криптографии используют различные способы усложнения аналитической структуры управляющих последовательностей.
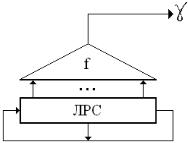
Первый способ заключается в усложнении процедуры формирования отдельных разрядов гаммы с помощью так называемого фильтрующего генератора (рис. 6.2. Фильтрующий генератор). «Фильтрующая» функция f выбирается из условия приближения закона распределения генерируемой последовательности к равномерному распределению и имеет высокую линейную сложность.
Рис. 6.2. Фильтрующий генератор
Другим способом синтеза псевдослучайных последовательностей «хорошего» качества стало применение в управляющем блоке нескольких линейных регистров сдвига. Генератор псевдослучайных
63
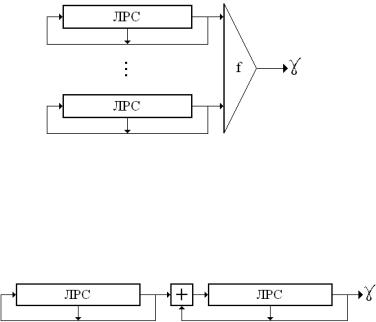
последовательностей, усложняющий структуру псевдослучайных последовательностей с помощью общей функции «отбора» разрядов гаммы, получил название комбинирующего генератора (рис. 6.3. Комбинирующий генератор).
Рис. 6.3. Комбинирующий генератор
Существенного увеличения периода гаммы позволяет достичь схема композиции нескольких линейных регистров сдвига (рис. 6.4. Композиция регистров сдвига).
.
Рис. 6.4. Композиция регистров сдвига
При использовании поточных шифров простой замены потеря или искажение отдельных символов шифртекста при его передаче по каналу связи приводит лишь к локальным потерям: все символы, принятые без искажений, будут расшифрованы верно. Это объясняется независимостью алгоритма шифрования от вида символов и их расположения в тексте.
Многоалфавитные поточные шифры также не распространяют ошибок при искажении отдельных символов шифртекста, но оказываются неустойчивыми к пропускам символов. В связи с этим в криптографических системах поточного шифрования приходится решать проблему синхронизации процедур зашифрования и расшифрования.
По способу решения этой проблемы поточные криптографические системы разделяют на синхронные и системы с самосинхронизацией.
Из-за простоты реализации, возможности достижения высоких скоростей преобразования в настоящее время широкое распространение получили поточные шифры, осуществляющие посимвольное зашифрование открытых сообщений с помощью некоторого множества преобразований замены. Очевидно, что для построения многоалфавитного поточного шифра замены необходимо указать его распреде-
64
литель (α, k), определяющий порядок использования шифрующих преобразований и собственно преобразования, т. е. простые замены, составляющие данный шифр.
В связи с этим криптографическая система поточного шифрования может быть представлена двумя основными блоками. Первый блок – управляющий, вырабатывает распределитель или, как говорят, управляющую последовательность. Второй блок – шифрующий, в соответствии с управляющей последовательностью реализует операции зашифрования текущего символа.
Как уже отмечалось, обычно под управляющей последовательностью понимают псевдослучайную последовательность – гамму, достаточную для однозначной идентификации преобразования и удобную с точки зрения практической реализации шифра.
Примеры криптографических систем поточного шифрования
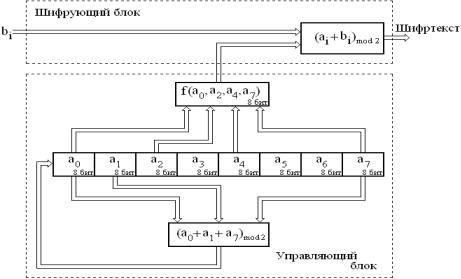
Криптографическая система поточного шифрования Д. Гиффорда (рис. 6.5. Система шифрования Гиффорда) была разработана в середине 80-х годов XX в., изготовлена в виде заказной микросхемы и более пяти лет использовалась для защиты конфиденциальной информации в агентстве Associated Press.
Управляющий блок криптосхемы представляет собой 64-битовый регистр сдвига с линейной обратной связью. Псевдослучайная последовательность формируется по схеме фильтрующего генератора; вид «фильтрующей» функции f образует один из секретных параметров шифра.
Рис. 6.5. Система шифрования Гиффорда
65
Шифртекст образуется в результате побайтного сложения кодов символов открытого текста с кодами управляющей гаммы.
Криптографическая система (протокол) А5 реализует поточный алгоритм шифрования данных, используемый для обеспечения конфиденциальности передаваемых речевых сообщений между мобильным телефоном и базовой станцией в европейской системе мобильной цифровой связи GSM (Group Special Mobile). Версия алгоритма А5/1 распространяется в Европе и США, версия А5/2 – в странах, не входящих в Евросоюз. В настоящее время разработана новая версия алгоритма А5/3 для использования в сетях 3G.
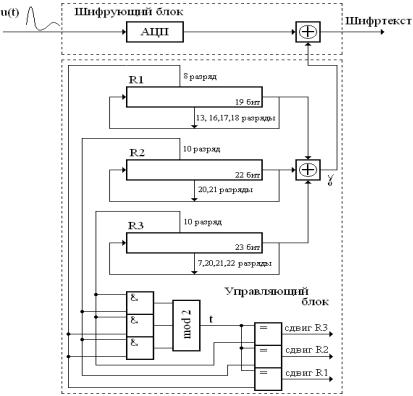
В системе А5 для выработки управляющей гаммы используется композиция трех регистров с линейными обратными связями.
Одной из особенностей алгоритма является реализация неравномерного движения информации регистров. Последовательность сдвига содержимого регистров определяется текущими значениями так называемых битов синхронизации – 8-го разряда первого регистра, 10-х разрядов второго и третьего регистров; сигналы сдвига каждого из регистров формируются с помощью соответствующей схемы управления. При этом в каждом такте работы системы осуществляется сдвиг содержимого регистра, значение синхробита которого совпадает со значением переменной t так, что в каждом такте выполняется, по меньшей мере, сдвиг двух регистров.
Зашифрование информации происходит в структурированном виде – цифровой поток речевого сигнала разбивается на кадры по 114 бит. Работа системы управляется 64-битовым секретным сеансовым ключом (рис. 6.6. Система шифрования А5), как обычно являющимся вектором инициализации. Значение криптографического ключа образуется на основе мастер-ключа, специфического для каждого пользователя, открытого 128-битового случайного числа и 22-битового номера кадра.
66
Рис. 6.6. Система шифрования А5
Иной подход к формированию управляющей гаммы предложен разработчиками стандарта шифрования ГОСТ 28147-89. В частности, авторы отказались от применения линейных регистров сдвига.
В соответствии с предложенным алгоритмом каждый элемент 64битовой гаммы представляется двумя 32-битовыми частями: младшей γм и старшей γс, которые обрабатываются независимо друг от друга. Формирование каждой из частей выполняется в соответствии со следующими рекуррентными выражениями:
γмi=(γмi-1+Cм)mod32, где Cм=01010101 (в шестнадцатеричной системе счисления);
γсi=(γсi-1+Cс-1)mod(32-1)+1, где Cс=01010104 (в шестнадцатеричной системе счисления).
Период повторения последовательности для младшей части гаммы составляет 232, старшей части – 232-1, для всей последовательности период равен 232·(232–1). Первая формула реализуется с помощью одной команды, вторая, несмотря на ее кажущуюся громоздкость, с помощью двух команд на всех современных 32-разрядных процессорах первой командой идет сложение по модулю 232 с запоминанием бита переноса, а вторая команда добавляет бит переноса к полученному значению.
Как обычно, начальный вектор инициализации процедуры в составе γм0 и γс0 выступает секретным параметром.
67
Ле к ц и я 7. СИСТЕМЫ ШИФРОВАНИЯ
СОТКРЫТЫМИ КЛЮЧАМИ
Системы шифрования с открытыми ключами или асимметричные системы шифрования появились относительно недавно. Их основу образуют так называемые однонаправленные (или односторонние) функции. Однонаправленной называется функция F: X→Y, для которой по x€X достаточно просто вычислить значение y=F(x), но обратное значение х по y€Y определить практически невозможно из-за вычислительной сложности задачи.
Криптографическая система RSA
Криптографическая система RSA была разработана в 1978 г. и в настоящее время является одной из самых распространенных систем шифрования с открытыми ключами. Свое название шифр получил в соответствии с первыми буквами фамилий авторов – Rivest, Shamir и Adleman. Напомним формальное описание шифра.
Пусть n=p·q – целое число, представленное в виде произведения двух простых чисел p и q. Пусть также М и С – блоки открытого и зашифрованого текстов, являются элементами множества натураль-
ных чисел (0, 1, … , (n-1)). |
|
Выберем числа e и d из условия: |
|
e·d≡1(mod φ (n)) , |
[1], |
где φ(n)=(p-1)·(q-1) – значение функции Эйлера от числа n. Пусть e – открытый ключ зашифрования, d – секретный ключ
расшифрования, а n – модуль системы; секретными параметрами шифра являются: p, q, d.
Тогда правила зашифрования и расшифрования определяются
формулами: |
|
С=E (M)=Me (mod n) |
[2] |
k |
|
М=D (C)=Cd (mod n) |
[3]. |
k |
|
Докажем справедливость M=Cd(mod n). |
|
Предварительно заметим (без вывода), что для любого целого числа М и любого простого p справедливо сравнение: Мp≡M(mod p) [4] (заметим, что сравнение [4] равносильно сравнению Мp–М≡0(mod p) или М·(Мp-1-1)≡0(mod p) [5]. Поскольку p – простое число, то
справедливы следующие рассуждения. Если наибольший общий делитель (M, p)=p, то p делит М, и поэтому М≡0 (mod p), откуда сле-
68
дует [5]. Если же наибольший общий делитель (M, p)=1, то согласно малой теореме Ферма Мp-1≡1(mod p), откуда также следует [5]).
Поскольку в [2] С есть остаток от деления Me на n, перепишем выражение [2] в виде соответствующего сравнения: С≡Me(mod n).
Поскольку любое целое число сравнимо с самим собой по любому модулю, в частности: q≡q(mod n), на основании свойств сравнений
(если a≡b(mod n) и c≡d(mod n), то ac≡bd(mod n)) имеем: q·С≡q·Me(mod n) или, учитывая, что n=p·q: q·С≡q·Me(mod q·p).
На основании свойств сравнений (если ac≡bc (mod nc), то a≡b (mod n)) это сравнение можно представить в виде: С≡Me(mod p).
Вновь, на основании свойств сравнений (если a≡b (mod n), то и ak≡bk (mod n)), запишем: Сd≡Med(mod p).
Аналогично можно показать, что Сd≡Med(mod q).
Итак: Сd≡Med(mod p) и Сd≡Med(mod q) [6]
В соответствии с [1] существует такое целое r, что e·d=r(p-1)·(q-
1)+1; отсюда:
Med=Mr(p-1)•(q-1)+1=M(rp-r)(q-1)+1=(Mp)r(q-1)·M-r(q-1)+1=(Mp)r(q-1)·M-r(q-1)·M.
Поскольку любое целое число сравнимо с самим собой по любому
модулю, а Мp≡M(mod p) (см. [4]) из последнего выражения следует:
Med=(Mp)r(q-1)·M-r(q-1)·M≡Mr(q-1)·M-r(q-1)·M(mod p) =M(mod p).
И окончательно: Med≡M(mod p); аналогично можно показать, что
Med≡M(mod q).
На основании свойств сравнений (если a≡b(mod n) и c≡d(mod n), то (a+c)≡(b+d)(mod n)) эти сравнения можно записать в виде:
0≡(-Med+ M)(mod p) и 0≡(-Med+M)(mod q) [7]
На основании свойств сравнений (если a≡b(mod n) и c≡d(mod n), то (a+c)≡(b+d)(mod n)), складывая левые и правые части сравнений
[6] и [7], имеем: Cd≡M(mod p) и Cd≡M(mod q).
Отсюда следует, что p и q являются множителями числа (Cd-М). Поскольку p и q – различные простые числа, это означает, что p·q также является множителем (Cd-М). Учитывая это и то, что n=p·q, можно записать: Cd≡M(mod n). Как известно, эта запись означает, что остатки от деления Cd и M на целое n одинаковы. Но по условию M<n, т. е. само М является остатком. Отсюда, окончательно, следует, что M=Cd(mod n), что и требовалось доказать.
Можно показать, что сложность нахождения секретного ключа системы RSA определяется сложностью разложения модуля n на простые множители. В настоящее время самые большие числа вида n=p·q,
69
которые удается разложить на множители известными методами, содержат в своей записи 140 десятичных знаков. В связи с этим рекомендуется выбирать p и q в размере 100 десятичных знаков каждое.
Криптографическая система Эль-Гамаля
Криптографическая система Эль-Гамаля была предложена в 1985 г. Приведем описание шифра.
Пусть р – простое число; α – специальная константа. Пусть также М и С – блоки открытого и зашифрованного текстов, являются элементами множества натуральных чисел (0, 1,..., (р-1)).
Параметр шифра ß определяется исходя из условия:
ß=αа (mod p), [1],
где a – целое число из интервала 1<а≤(р-2), выбираемое владельцем секретного ключа.
Пусть k=(α, ß, p, a) – выбранный ключ, который состоит из открытого ключа зашифрования kз=(α, ß, p) и секретного ключа расшифрования kр=a.
Правило зашифрования на ключе kз определяется формулой:
Ek(M)=(C1, C2) |
[2], |
где C1=αr (mod p), C2=ßr·M (mod p) |
[3]; |
r – случайное число (рандомизатор) из интервала 1≤r≤(р-2), выбираемое пользователем, который выполняет зашифрование открытого текста.
Отметим, что при зашифровании каждый блок открытого текста представляется двумя блоками зашифрованного текста.
Правило расшифрования на ключе kр устанавливается формулой: |
|||
D (C , C )=C - a·C |
2 |
(mod p) |
[4]. |
k 1 2 1 |
|
|
|
Покажем, что М=Dk(C1, C2). Для этого в выражение [4] подставим
значения C1 и C2 из [3]. С учетом [1] имеем: |
|
C1-a·C2 =α-аr(mod p)·(ßr·M)(mod |
p)≡≡α-аr·ßr·M(mod p)≡α- |
аr·(αа)r·M(mod p)=М(mod p) |
[5]. |
Учитывая, что M<p (т. е. само М в выражении [5] является остат-
ком) из [5], имеем: M=C1- a·C2 (mod p)=Dk(C1, C2).
Криптографическая стойкость системы шифрования Эль-Гамаля определяется сложностью решения задачи дискретного логарифмирования элементов конечного поля (логарифмирования в пространстве модулей). Утверждается, что в настоящее время эта задача практически нереализуема для простых чисел, содержащих не менее 150 десятичных знаков. Шифр Эль-Гамаля относят к шифрам с вероятност-
70
ной схемой зашифрования, поскольку результат зашифрования, в частности, определяется значением рандомизатора.
Схемы применения асимметричных криптографических систем
Итак, асимметричные криптографические системы используют два существенно различающихся ключа для зашифрования и расшифрования. При этом каждый пользователь подобной системы, на-
пример А, получает в свое распоряжение два именных ключа: kоткрА и kзакрА. Один из ключей (kоткр) не составляет секрета, он выступает в
качестве публичного и называется открытым; второй ключ (kзакр) традиционно является секретным. Знание одного ключа практически не позволяет определить значение второго.
Особенностью применения ключей асимметричных криптографических систем является следующее: любой из ключей может исполь-
зоваться для зашифрования информации, при этом ее расшифрование возможно и обязательно осуществляется парным ключом.
1. Схема отсылки пользователем А пользователю В секретного сообщения и расшифрования полученного сообщения:
А → В |
С=E |
откр |
(М) |
|
k |
B |
|
В |
М=DkзакрB (C). |
||
2. Схема отсылки пользователем А пользователю В сообщения с подтверждением авторства и проверки полученного сообщения:
А → В |
С=E закр |
А |
(М) |
|
k |
|
|
В |
М=DkоткрА (C). |
||
3. Схема отсылки пользователем А пользователю В секретного сообщения с подтверждением авторства:
А → В |
С=E откр |
(E закр |
А |
(М)) |
|
k |
B k |
|
|
В |
М= DkоткрА (DkзакрB (C)). |
|||
Как следует из рассмотренного материала, в асимметричных криптографических системах основные операции зашифрования и расшифрования образуют возведение в степень, умножение, деление, т. е. «длинные» компьютерные операции. Напомним, что для симметричных криптографических систем характерно использование «коротких» компьютерных операций: сложения, сдвигов, табличных замен. В связи с этим на практике симметричные криптографические системы преимущественно применяются для защиты данных (больших объемов информации), асимметричные – для защиты криптографических ключей, реализации электронной цифровой подписи.
