Щерба В.В. Криптографическая защита информации

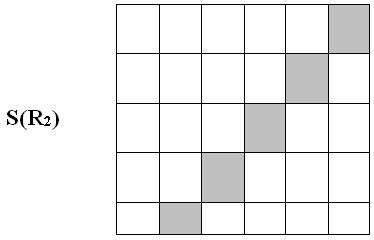
51

Рис. 4.3. Отношение S(R2)

Модель шифра простой замены

Пусть множества M и C €UAi для 1≤i≤L и пусть любое отображение k задается подмножеством множества R(A) симметричных бинарных отношений подстановки множества А. Тогда для любого k, открытого текста m=(m1, … mL) и шифрованного текста c=(c1, …cL) правила зашифрования и расшифрования шифра простой замены определяются формулами:

Еk(m)=(k(m1), … k(mL)); Dk(c)=(k-1(c1), … k-1(cL)),

где k-1 – отображение, обратное к k.

Модель шифра перестановки

Пусть множества M и C €AW и пусть любое отображение k задается подмножеством множества R(W) симметричных бинарных отношений подстановки множества {1, 2, … W}. Тогда для любого k, открытого текста m=(m1, … mW) и шифрованного текста c=(c1, …cW) правила зашифрования и расшифрования шифра перестановки определяются формулами:

Ek(m)=(mk(1), … mk(W));

Dk(c)=(сk-1(1), … сk-1(W)),

где k-1 – отображение, обратное к k.

Модель асимметричного шифра RSA

Основу асимметричных систем шифрования образуют так называемые однонаправленные (или односторонние) функции. Однонаправленной называется функция F:X→Y, для которой по x€X доста-

52

точно просто вычислить значение y=F(x), но обратное значение х по y€Y вычислить практически невозможно. В частности, такими функциями являются операции приведения числа по модулю.

Для лучшего уяснения деталей модели напомним некоторые положения модулярной арифметики.

Пусть a и n – натуральные числа. Разделить число a на число n с остатком означает найти такие целые числа q и r, что:

a=nq+r, где 0≤r< n.

При этом число q называют неполным частным, а r – остатком от деления. Если остаток r равен нулю, то говорят, что число n делит число a нацело, или n является делителем числа a.

Операцию нахождения числа r называют приведением числа а по модулю n; она записывается в виде: r=a (mod n).

Тот факт, что числа a и b имеют одинаковые остатки при делении на натуральное число n, немецкий математик Карл Фридрих Гаусс предложил записывать следующим образом:

a≡b (mod n) (читается: «a сравнимо с b по модулю n»).

Примеры: 2006≡2 (mod 4); 8k+1≡1 (mod 8)

Очевидно, что a≡b (mod n) в том и только в том случае, когда a–b делится на n.

Докажем необходимое и достаточное условие сравнимости. Пусть r (0≤r<n) – остаток от деления натуральных a и b на n. Тогда a и b можно представить в виде, соответственно, a=nq+r и b=np+r. Образуем разность a–b:

a–b=(nq+r)-(np+r)= nq+r-np-r=nq-np=n(q-p) [1].

На основании [1] очевидно, что a–b делится нацело на n, что и требовалось доказать.

Сравнения обнаруживают свойства, во многом похожие на свойства равенств. Равенства можно складывать друг с другом, вычитать одно из другого, умножать – в результате получается верное равенство. То же самое справедливо для сравнений.

Если произвольные целые числа a, b, c, d таковы, что a сравнимо с b, а c сравнимо с d по модулю n, то по этому же модулю сравнимы числа a+c и b+d, a-c и b-d и ac и bd.

Докажем первое свойство. Пусть a≡b (mod n) и с≡d (mod n). Тогда a-b делится на n и с-d делится на n. Поскольку (a+c)-(b+d)=(a-b)- (c-d), то и (a+c)-(b+d) делится на n. Отсюда на основании необходи-

53

мого и достаточного условия сравнимости можно записать: (a+c)≡(b+d) (mod n), что и требовалось доказать.

Докажем третье свойство. Пусть a≡b (mod n) и с≡d (mod n). Тогда, a-b делится на n и с-d делится на n. Поскольку ac-bd=ac-bc+bc- bd=c(a-b)+b(c-d), то ac-bd делится на n. Отсюда на основании необходимого и достаточного условия сравнимости можно записать: ac≡bd (mod n), что и требовалось доказать.

Операция возведения в натуральную степень сводится к многократному умножению, в связи с чем из последнего свойства следует:

если a≡b (mod n), то и ak≡bk (mod n).

Известно, что левую и правую часть равенства можно разделить на одно и то же не равное нулю число. В пространстве сравнений аналогичное свойство формулируется более жестко, а именно:

Если числа c и n взаимно просты и ac≡bc (mod n), то a≡b (mod n).

Докажем это свойство. Из первого сравнения следует, что ac-bc делится на n. Но ac-bc=с(a-b), т. е. произведение двух сомножителей

си (a-b)делится на n. Поскольку c на n не делится (c и n – взаимно простые числа), это означает, что нацело на n делится второй сомножитель (a-b). Отсюда на основании необходимого и достаточного условия сравнимости можно записать: a≡b (mod n), что и требовалось доказать.

Сдругой стороны, обе части сравнения можно разделить на одно и то же число одновременно с модулем. Если ac≡bc (mod nc), то a≡b (mod n).

Докажем это свойство. Из первого сравнения следует, что ac-bc делится на nc. Но ac-bc=с(a-b), т. е. произведение двух сомножителей

си (a-b)делится нацело на nc. Но это означает, что (a-b) делится нацело на n. Отсюда на основании необходимого и достаточного условия сравнимости можно записать: a≡b (mod n), что и требовалось доказать.

И еще некоторые сведения из теории чисел. Натуральное число а, большее единицы, называется простым, если оно не имеет натуральных делителей, отличных от единицы и самого числа а. Наибольшее целое число, делящее одновременно целые числа a и b, называется их наибольшим общим делителем и обозначается как (a, b). Если (a, b)=1, то a и b называются взаимно простыми числами. Любое нату-

ральное число, отличное от единицы, либо является простым, либо может быть представлено в виде произведения простых чи-

54

сел. Это представление определено однозначно с точностью до порядка сомножителей в произведении.

Следует отметить, что в настоящее время не существует достаточно эффективных алгоритмов разложения произвольного целого числа на простые множители даже в случае, когда известно, что число может быть представлено произведением двух простых чисел. Отсутствие эффективных алгоритмов с доказуемыми оценками сложности позволяет использовать это свойство для решения различных задач криптографии.

Модель шифра RSA

Пусть n=p·q – целое число, представленное в виде произведения двух больших простых чисел p и q. Пусть также М и С – блоки открытого и зашифрованого текстов – являются элементами множества натуральных чисел (0, 1, … , (n-1)).

Выберем числа e и d из условия: e·d≡1(mod φ(n)), где φ(n)=(p- 1)·(q-1), значение функции Эйлера от числа n.

Тогда правила зашифрования и расшифрования определяются

формулами:

Ek(М)=Мe(mod n) и Dk(С)=Сd(mod n) (или: Ek(М)=Мd(mod n) и Dk(С)=Сe(mod n)).

При этом k=(n, p, q, e, d) – выбранный ключ шифра, который состоит из публичного ключа kоткр=(n, e) и секретного ключа kзакр=(n, d), где секретными параметрами являются p, q и d.

55

Л е к ц и я 5. БЛОЧНЫЕ СИСТЕМЫ ШИФРОВАНИЯ

Особенности современного построения блочных шифров

В настоящее время построение блочных шифров в значительной степени осуществляется с использованием итеративных криптографических алгоритмов, наиболее органичных для исполнения с помощью современных программно-аппаратных средств. При этом реализация подобного алгоритма представляет собой многократное выполнение некоторых базовых преобразований над блоками открытых или зашифрованных сообщений.

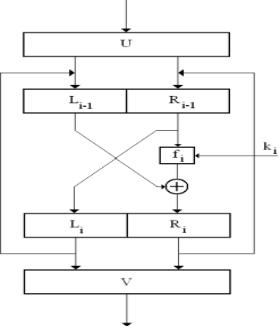
Многие современные алгоритмы блочных систем шифрования в качестве основы преобразования информации используют разновидности так называемой сети Фейстеля (рис. 5.1. Структурная схема сети Фейстеля).

Рис. 5.1. Структурная схема сети Фейстеля

Преобразование, реализуемое сетью на i-ом цикле шифрования, представляется выражением: Li=Ri-1 [1], Ri=Li-1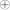 fi(Ri-1, ki) [2]. Выра-

жая Ri-1 из [1] и подставляя в [2], имеем: Ri-1=Li и Li-1= Ri fi(Li, ki). Эти выражения иллюстрируют свойство обратимости преобразования

сети Фейстеля.

Алгоритм шифрования DES и режимы его использования

DES осуществляет шифрование 64-битовых блоков данных с помощью 56-битового ключа. Процесс преобразования каждого блока

56

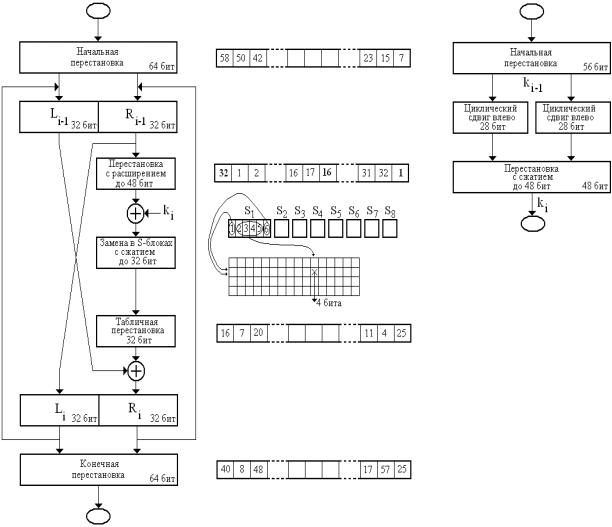
включает начальную и конечную перестановки битов блока, а также 16 циклов шифрования, образованных комбинацией стандартных перестановок и замен (рис. 5.2. Структурная схема алгоритма DES).

Рис. 5.2. Структурная схема алгоритма DES

Для решения разных криптографических задач блочные шифры могут использоваться в различных режимах. Например, разработчики шифра DES рекомендуют четыре основных режима применения шифра.

Режим реализации представленного выше алгоритма без какихлибо изменений и дополнений носит название режима электронной кодовой книги ECB (Electronic Code Book). Здесь правила зашифрования и расшифрования блоков данных выглядят как Ci=DESk(Мi) и Мi=DESk(Ci). Достоинством режима является простота реализации, отсутствие распространения ошибок при использовании плохих каналов связи – искажение при передаче 64-битового блока Сi шиф-

57

ртекста приводит к получению ошибочного значения только соответствующего блока Mi. В качестве недостатка обычно упоминается возможность эффективного криптоанализа, связанного с малым объемом шифруемых блоков, в частности, текстовых сообщений, когда идентичные по содержанию блоки открытого текста порождают одинаковые блоки шифртекста.

Врежиме сцепления блоков CBC (Cipher Block Chaining) каждый

блок открытого текста Mi перед зашифрованием складывается по mod2 с предыдущим блоком зашифрованного текста Ci. Здесь правила зашифрования и расшифрования задаются выражениями:

Ci=DESk(MiCi-1), Mi=DESk(Ci)Ci-1; начальное значение С0 (начальный вектор – Initial Vector) выступает дополнительным секретным параметром шифра. Искажение при передаче зашифрованного блока

Сi приводит к появлению двойной ошибки при расшифровании блоков Ci и Ci+1. В то же время изменение блока Mi приводит к искажению не только блока Ci, но и всех последующих блоков шифртекста. Это свойство режима может использоваться для контроля целостности передаваемых сообщений М, кодом аутентификации которых будет являться CN.

Врежиме обратной связи по шифртексту CFB (Cipher Feed Back)

формируется некая блочная гамма Z0, Z1, … Zn в соответствии с выражением Zi=DESk(Ci-1). Правила зашифрования и расшифрования задаются выражениями: Ci=Mi Zi и Mi=Ci Zi. Свойства режима схожи со свойствами предыдущего режима.

Алгоритм шифрования ГОСТ 28147-89 и режимы его использования

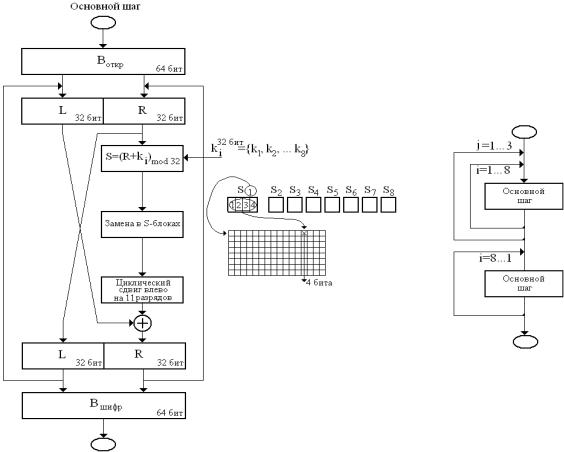
ГОСТ выполняет шифрование 64-битовых блоков данных под управлением составного ключа k1, …k8 длиной 32-бита каждый; таким образом, общая размерность ключа шифра составляет 256 бит, число циклов – 32 (рис. 5.3. Структурная схема алгоритма ГОСТ).

58

Рис. 5.3. Структурная схема алгоритма ГОСТ

Режим замены – это режим реализации алгоритма ГОСТ без ка- ких-либо изменений и дополнений.

Возможность обработки неполного блока данных размером меньше 64 бит предоставляется каждым из режимов гаммирования, что существенно при шифровании массивов с произвольным размером.

В режиме гаммирования формируется некая блочная гамма Z0, Z1, … Zn в соответствии с выражением Zi=ГОСТk(Zi-1). Правила зашифрования и расшифрования режима задаются выражениями: Ci=Mi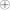Zi и

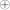Mi=CiZi.

Режим гаммирования с обратной связью отличается от предыдущего способом выработки элементов гаммы, очередной элемент гаммы вырабатывается как результат преобразования предыдущего блока зашифрованных данных. Этим достигается зацепление блоков: каждый блок шифртекста в этом режиме зависит от соответствующего и всех предыдущих блоков открытого текста. Поэтому данный режим иногда называется гаммированием с зацеплением блоков. Правила

59

зашифрования и расшифрования режима задаются выражениями:

Ci=Mi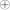ГОСТk(Ci-1) и Mi=Ci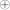ГОСТk(Ci-1).

Преимущества стандарта ГОСТ в сравнении с DES:

–фактическое отсутствие аналитических методов анализа;

–более чем 4-кратное превышение объема ключа и 2-кратное превышение циклов шифрования;

–примерно в 2 раза большее быстродействие в расчете на «короткие» операции за счет отсутствия нерегулярных битовых перестановок.

60

Л е к ц и я 6. ПОТОЧНЫЕ СИСТЕМЫ ШИФРОВАНИЯ

Особенности построения современных поточных шифров

Выше отмечалось, что одним из первых и наиболее известных в истории криптографии шифров поточного шифрования стал шифр гаммирования Вернама. В 1917 г. сотрудник американской телеграфной компании Г. Вернам предложил идею, а позже создал устройство автоматического шифрования телеграфных сообщений. Устройство осуществляло электромеханическое сложение по mod2 пятиразрядных кодов телеграфных символов Бодо с кодами гаммы, предварительно нанесенными на склеенную в кольцо телеграфную перфоленту. На основании свойства обратимости операции сложения по mod2 расшифрование сообщения выполнялось с помощью аналогичного устройства сложением шифртекста с той же гаммой.

Код сообщения «VERNAM» 01111 10000 01010 00110 11000 00111 МТК-2

Код сообщения «VERNAM» 01111 10000 01010 00110 11000 00111 МТК-2

Безусловными достижениями шифра Вернама стали автоматизация процесса преобразования сообщений и, фактически, объединение процедур зашифрования и расшифрования информации и ее передачи по каналу связи, исключившие процедуру предварительного шифрования.

Интуитивно понятно, что стойкость шифра в значительной степени определялась качеством его ключевого элемента – гаммы. Код гаммы выбирался случайно, но при зашифровании длинных сообщений он регулярно повторялся, что, очевидно, является недопустимым. Попытки увеличить гамму приводили к неудобствам работы с длинным кольцом телеграфной перфоленты. Тогда был предложен вариант работы с двумя кольцевыми перфолентами, с помощью одной из которых шифровалась другая. В результате период повторения гаммы был существенно увеличен. Вместе с тем, трудности изготовления,