
Щерба В.В. Криптографическая защита информации
.pdf
41
Л е к ц и я 3. КЛАССИФИКАЦИЯ И ВИДЫ ШИФРОВ
Общая классификация шифров по разным основаниям
Исходно шифры целесообразно классифицировать по виду преобразования, которое применяется к открытому тексту в процессе шифрования. Как отмечалось выше, если фрагменты открытого текста (символы или их сочетания) при шифровании заменяются некими эквивалентами, то такой шифр относится к классу шифров замены. Если символы открытого текста при шифровании меняются местами друг с другом, то это – шифр перестановки. С целью повышения стойкости шифрованный текст, полученный с помощью одного шифра, может быть зашифрован повторно с применением другого шифра. Подобные композиции различных шифров образуют третий класс шифров – композиционные шифры (рис. 3.1. Классификация шифров).
Рис. 3.1. Классификация шифров
Классификация шифров замены. Фрагменты открытого текста,
подлежащие при зашифровании замене, обычно называют шифрвеличинами, их заменители – шифробозначениями. Пусть U=(u1, u2, … uN) – множество возможных шифрвеличин, V=(v1, v2, … vM) – множество возможных шифробозначений. Тогда правило зашифрования может быть представлено в виде: vi=E(ui).
В общем случае для обеспечения однозначности расшифрования число шифробозначений не должно быть меньше числа шифрвеличин, т. е. М≥N.
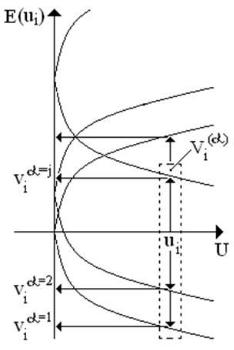
Пусть множество возможных шифрвеличин представляется множеством целых чисел, а в качестве правила зашифрования используется vi=E(ui)=√ui+α, где 1≤α≤r, где r€N. Тогда в соответствии с vi=E(ui) значение vi может выбираться из разных множеств Vi, в частности, для различных значений параметра α. Таким образом, в общем
42
случае функция зашифрования E(ui) может являться многозначной (рис. 3.2. Многозначность функции зашифрования E(ui).
Рис. 3.2. Многозначность функции зашифрования E(ui)
Если 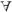 α, i имеет место│Vi(α)│=1, то такой шифр называется шифром однозначной замены, если же
α, i имеет место│Vi(α)│=1, то такой шифр называется шифром однозначной замены, если же 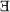 α, i такие, что│Vi(α)│>1, то шифр называется шифром многозначной замены.
α, i такие, что│Vi(α)│>1, то шифр называется шифром многозначной замены.
Шифры однозначной и многозначной замены могут быть шифрами равнозначной и разнозначной замены. Если для алфавита закрытого текста В и некоторого целого q€N и 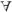 i выполняется условие vi€Bq, то соответствующий шифр называется шифром равнозначной замены, в противном случае – разнозначной замены.
i выполняется условие vi€Bq, то соответствующий шифр называется шифром равнозначной замены, в противном случае – разнозначной замены.
Шифры однозначной и многозначной, равнозначной и разнозначной замены могут быть одноалфавитными и многоалфавитными. Если параметр r=1, шифр называется шифром одноалфавитной замены или шифром простой замены, в противном случае – многоалфавитным шифром замены.
Шифры обоих столбцов классификации могут быть симметричными при kз=kр или асимметричными, если kз≠kр (рис. 3.3. Классификация шифров).
В большинстве случаев для алфавита открытого текста А множество шифрвеличин U является подмножеством множества Ap для некоторого целого p€N. Если p=1, соответствующие шифры называют поточными шифрами замены, при p>1 – блочными шифрами замены.
43
Другими словами, если открытый текст перед зашифрованием разбивается на блоки, состоящие из нескольких знаков, и исходный текст обрабатывается по блокам, – это блочный шифр. Если каждый знак открытого сообщения шифруется отдельно, то такой шифр – поточный.
Вместе с тем, необходимо отметить, что сегодня разделение шифров на поточные и блочные в большей степени связано не с мощностью используемого алфавита, а с алгоритмическими и техническими особенностями реализации шифрующих преобразований. Например, рост производительности и разрядности процессоров позволяет в настоящее время определять как поточные шифры, в которых используются алфавиты мощностью 232 и 264.
Рис. 3.3. Классификация шифров
Классификация шифров перестановки
В шифрах перестановки преобразование открытого текста выполняется путем закономерного изменения порядка следования символов в соответствии с используемым ключом.
44
Очевидным способом указания последовательности перестановки символов является задание необходимой закономерности с помощью таблицы; соответствующие шифры получили название шифров табличной перестановки.
Широкое распространение получили шифры так называемой маршрутной перестановки. В них фрагменты текста записываются в шаблон в соответствии с одной траекторией и для получения зашифрованного текста считываются согласно другой траектории. Например, открытое сообщение может быть построчно записано в прямоугольную таблицу, а для получения закрытого текста – считано по столбцам. Такая разновидность маршрутных шифров получила название столбцовых (строчных) перестановок. Например, преобразование открытых текстов в зашифрованные и наоборот может выполняться с использованием различных поворотных решеток и т. п. Эту разновидность маршрутных шифров стали называть лабиринтными.
Стойкость шифров
Надежность, или стойкость, шифров – это их способность противостоять попыткам определения содержания шифрованных сообщений. Очевидно, ее можно оценить объемом работы, необходимой для вскрытия конкретного шифра. Исходная информация для вскрытия шифра, возможности и цели противника могут быть разными. Очевидно, основной целью криптографического анализа может считаться получение конфиденциальной информации, однако в ряде случаев целью нападения может быть и используемый криптографической системой секретный ключ.
В криптографии с секретными ключами обычно рассматривают следующие основные виды криптографических атак.
1. Атака на основе шифртекста. Противник располагает шифртекстами сi=Ek(mi), в соответствии с неизвестными открытыми сообщениями mi, которые получены с помощью различных криптографических ключей k. Задачей анализа выступает получение хотя бы одного открытого сообщения mi или соответствующего криптографического
ключа ki.
2. Атака на основе известного открытого текста. Противник располагает парами (mi, ci) открытых и соответствующих им шифрованных сообщений. Задачей анализа является определение значения ki, по крайней мере, для одной из пар сообщений. В частности, когда
45
k1=k2= …=km, требуется определить значение k или, по крайней мере, текст нового сообщения xm+1, зашифрованного на том же ключе.
3.Атака на основе выбранного открытого текста. Эта атака отличается от предыдущей тем, что противник имеет возможность выбора открытого текста и получения соответствующего зашифрованного сообщения. Цель анализа – получение значения k. Подобная атака возможна, например, в ситуации, когда противник имеет доступ к шифратору передающей стороны.
4.Атака на основе выбранного шифртекста. Эта атака отличается от второй тем, что противник имеет возможность выбора шифртекста
иполучения соответствующего открытого сообщения. Цель анализа – получение значения k. Такая атака возможна, если противник имеет доступ к шифратору принимающей стороны.
При этом предполагается, что выполняется принцип Кирхгоффса, а именно: противник располагает исчерпывающими сведениями об использованной криптографической системе, стойкость шифра должна определяться только секретностью использованного криптографического ключа.
В действительности истории криптографии известно лишь небольшое число случаев соблюдения этого принципа. В подавляющем большинстве ситуаций для увеличения степени неопределенности противника, усложнения соответствующего анализа любая «чувствительная» информация о криптографической системе закрывается. Одним из противоположных примеров является американский стандарт шифрования конфиденциальной информации DES, сведения о котором были опубликованы и широко обсуждались специалистами.
В криптографии рассматривается теоретическая и практическая стойкость шифров. В рамках первого направления исследуются и доказываются аналитические условия построения так называемых теоретически стойких или совершенных шифров. При этом совершенными называются шифры, для которых любой анализ шифртекстов не раскрывает никакой информации о соответствующем открытом тексте, за исключением, возможно, его размера.
Существование подобных шифров доказывается в одной из теорем Шеннона, однако ценой этой стойкости является необходимость использования для шифрования каждого сообщения случайного равновероятного ключа, не меньшего по размеру самого сообщения. Во всех случаях, за исключением ряда особых, эта цена чрезмерна, по-
46
этому на практике в основном используются шифры, не обладающие абсолютной стойкостью.
Таким образом, большинство применяемых в практике шифров может быть раскрыто за конечное время или, точнее, за конечное число шагов или операцией. В связи с этим особое значение имеет понятие практической стойкости, выражающее практическую трудность их раскрытия. Количественной мерой этой трудности может служить число элементарных арифметических и логических операций, которые необходимо выполнить, чтобы раскрыть тот или иной шифр.
В отсутствие универсальной методики испытаний определение практической стойкости шифров, как правило, осуществляется экспериментально путем проведения различных криптографических атак группой высококвалифицированных специалистов с достаточным техническим оснащением.
На государственном уровне оценка стойкости шифров выполняется уполномоченными организациями. В нашей стране аксиоматическим и нормативно закрепленным экспертом в сфере криптографической защиты информации является ФСБ Российской Федерации.
47
Л е к ц и я 4. ФОРМАЛЬНЫЕ МОДЕЛИ ШИФРОВ
Алгебраическая модель шифра
Понятие «множество» является первичным, а значит, неопределяемым понятием дискретной математики. В связи с этим будем считать множеством совокупность поименованных элементов.
Множества бывают счетные и бессчетные, конечные и бесконечные. Множество Ма называется подмножеством множества Мb, если каждый элемент множества Ма является элементом множества Мb: Ма€Мb. Само множество Мb является своим подмножеством: Мb€Мb. Всякое другое подмножество Ма множества Мb является собственным подмножеством множества Мb. Число элементов, образующих конечное множество, называется его мощностью │Ма│.
Множество элементов, которые принадлежат и множеству Ма, и множеству Мb, называется пересечением множеств Ма и Мb: Мa∩Мb. Множество элементов, которые принадлежат либо множеству Ма, либо множеству Мb, либо и множеству Ма, и множеству Мb, называется объединением множеств Ма и Мb: МaUМb. Множество элементов, которые принадлежат множеству Ма и не принадлежат множеству Мb, называется разностью множеств Ма и Мb: Мa\Мb.
Декартовым произведением Ма·Мb множеств Ма и Мb называется множество М вида:
М=(mi, mj) при условии, что mi €Ма и mj €Мb,
где (mi, mj) – последовательность двух элементов, в которой порядок их записи важен.
Аналогично понятию декартова произведения двух множеств определяется декартово произведение n множеств. Декартовым произ-
ведением М1·М2· … ·Мn = ∏Mi для 1≤i≤ n множеств М1, М2, … Мn называется множество:
М=(mi1, mi2, … min) при условии, что mi1 €М1, mi2 €М2, … min
€Мn.
Таким образом, элементами декартова произведения М1·М2· … ·Мn являются всевозможные последовательности, каждая из которых состоит из n элементов, причем первый элемент принадлежит множеству М1, второй – множеству М2, n-ый элемент – множеству Мn.
Частным случаем декартова произведения является квадрат множества. Квадратом М2 множества М называется декартово произведе-
48
ние Ма·Мb множеств Ма и Мb, в котором сомножители Ма, Мb равны
друг другу Ма=Мb=М.
Отображением f множества А в множество В называется правило, согласно которому каждому элементу а€А ставится в соответствие определенный и единственный элемент b€B; отображение обозначается в виде: f: А→В (рис. 4.1. Диаграмма Эйлера-Венна).
Рис. 4.1. Диаграмма Эйлера-Венна
Элементы множества А называются прообразами, а элементы множества В – образами отображения f. Можно отметить, что отображение как бы «расширяет» область определения, область значений привычной математической функции, включающими только числовые значения, областью любых объектов; в этом смысле понятие отображения является обобщением понятия функции.
Если прообразом каждого элемента множества В является не более одного элемента множества А, то отображение называется вложением или инъективным отображением. Таким образом, если f:А→В – вложение, то множество А можно как бы вложить в множество В в качестве его подмножества. Если для любого b€B прообраз не пуст, то f:А→В – наложение или сюръективное отображение. Другими словами, отображение f:А→В является наложением, если в В отсутствуют «лишние» элементы. Отображение, которое одновременно является вложением и наложением, называется взаимно однозначным, биективным отображением или биекцией.
Пусть М, K, С – конечные, счетные множества возможных открытых текстов, ключей и шифрованных текстов соответственно.
Пусть также Ek: М→С – правило (отображение) зашифрования на ключе k€K.
Пусть Dk: Ek(M)→M – правило расшифрования на ключе k€K.
49
Шифром (шифросистемой) назовем совокупность ∑А=(M, K, C, E, D) введенных множеств, для которых выполняются следующие свойства:
–для любых m€M и k€K выполняется равенство Dk(Ek(m))=m. Очевидно, что выполнение свойства обеспечивает однозначность расшифрования;
–C=UEk(M) для k€K. Это свойство означает, что любой элемент c€C может быть представлен в виде Ek(m) для подходящих элементов m€M и k€K.
Отметим, что в общем случае утверждение – «для любых k€K и
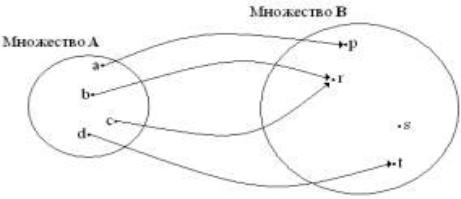
c€C выполняется равенство Ek(Dk(c))=c» – является неверным. Покажем несостоятельность введенного утверждения (рис. 4.2.
Диаграмма Эйлера-Венна). На основании второго свойства алгебраической модели следует, что для произвольных k€K множество С представляет собой объединение, в общем случае, несовпадающих
множеств Ck. Рассмотрим подмножество множества Ci, не совпадающее с множеством Cj. Выберем произвольный элемент с* выделенного подмножества. Предположим, что Dj(c*)=m* и, следовательно, Ej(m*)=c*. Однако исходя из условия Ej(m*)=c**, где c**€Cj, образу m* поставлены в соответствие два прообраза. Таким образом, в силу сделанных предположений, образу m* поставлены в соответствие два различных прообраза c* и c**. Это означает, что конструкция
Ek: М→С не является отображением, что противоречит введенной алгебраической модели шифра.
Рис. 4.2. Диаграмма Эйлера-Венна
50
Заметим, что из первого свойства модели следует свойство инъективности отображения Ek. Другими словами, если m1, m2 €M, причем m1≠m2, то при любом k€K выполняется условие Ek(m1)≠Ek(m2).
В большинстве случаев множества М и С представляют собой объединения декартовых степеней некоторых множеств А и В, соответственно так, что для некоторых натуральных L и L1:
для 1≤i≤L, для 1≤i≤ L1 Множества А и В называют соответственно алфавитом открытого
текста и алфавитом шифрованного текста. Другими словами, открытые и шифрованные тексты записываются привычным образом в виде последовательности символов.
Фундаментальным понятием дискретной математики является понятие бинарного отношения, которое используется для обозначения связи между объектами или понятиями.
Бинарным отношением R2 на множестве М называют подмножество его квадрата: R2€M2. При этом говорят, что элементы mi и mj находятся в отношении R2, если (mi, mj) € R2.
Симметричным называется бинарное отношение R2 на множестве М, такое, что если (mi, mj)€R2, то и (mj, mi) также находится в отно-
шении R2, т. е. (mj, mi)€R2.
Проиллюстрируем симметричное бинарное отношение замены на примере шифра АТБАШ. Напомним, что в нем правило зашифрования состояло в замене i-ой буквы алфавита буквой с номером n–i+1, где n – число букв алфавита. Другими словами, первая буква алфавита, присутствующая в открытом тексте, заменялась последней буквой алфавита, вторая буква алфавита – предпоследней и т. д. Для упрощения рассмотрим алфавит, состоящий всего из пяти букв А = (a, b, c, d, e).
Для задания бинарного отношения воспользуемся так называемой матрицей смежности. При матричном задании отношения используют двумерную таблицу, каждой строке (столбцу) которой взаимно однозначно сопоставляется элемент множества А. Тогда каждая ячейка таблицы с индексами (i, j) взаимно однозначно соответствует множеству А2. Ячейку, которая соответствует элементу, принадлежащему R2€A2, как-то помечают, например, заштриховывают или вписывают единицу, остальные ячейки оставляют чистыми или заполняют нулями. В этих предположениях матрица смежности S(R2) шифра, определяющая рассматриваемое отношение, имеет следующий вид (рис. 4.3. Отношение S(R2).
