
- •ВВЕДЕНИЕ
- •1. СОСТОЯНИЕ ВОПРОСА И ЗАДАЧИ ИССЛЕДОВАНИЯ
- •1.1. Классификация зимних автомобильных дорог
- •1.2. Конструкции, методы проектирования и строительства ледовых переправ и автозимников
- •1.3. Свойства геосинтетических материалов, применяемых для армирования дорожных конструкций
- •Выводы по первой главе
- •2.1. Особенности свойств льда, как материала дорожного покрытия, его физико-механические свойства
- •2.2. Особенности поведения льда под нагрузкой
- •2.3. Анализ напряжённого состояния армированных ледяных образцов-балок в процессе разрушения
- •2.4. Методы определения несущей способности ледового покрова
- •2.5. Оценка несущей способности армированного ледового покрова
- •Выводы по второй главе
- •3.4. Результаты лабораторных испытаний геосинтетических материалов
- •Выводы по третьей главе
- •4.3. Наблюдение за опытным участком и испытания ледового покрова
- •4.4. Извлечение армирующего материала из ледового покрова
- •4.6. Строительство опытных участков на реальных объектах
- •Выводы по четвёртой главе
- •ЗАКЛЮЧЕНИЕ И ОБЩИЕ ВЫВОДЫ
- •Библиографический список

2.3. Анализ напряжённого состояния армированных ледяных образцов-балок в процессе разрушения
Рис. 2.9. Расчётная схема действия нагрузок: F – сила, приложенная к образцу; l – расстояние между опорами
Для оценки эффективности применения геосинтетических материалов в качестве арматуры для льда был выполнен расчёт на прочность ледяных образцов балок. На рис. 2.9 представлена схема действия нагрузок на обра- зец-балку. Поперечное сечение балки – прямоугольник (рис.2.10).
|
|
|
|
И |
|
|
|
Д |
|
|
|
А |
|
|
|
б |
|
|
|
Рис |
|
|
|
|
С |
|
|
|
|
. 2.10. Поперечное сечение образца: Y, Z – главные центральные оси площади А;
Z1 – главная центральная ось площади А1; С – центр тяжести площади А1
Данная схема испытаний моделирует наиболее опасный случай работы льда под нагрузкой: участки, где лёд завис над водой (а не плавает в ней).
Площадь поперечного сечения образца, м2,
A bh, |
(2.1) |
где b – ширина поперечного сечения образца, м; h – высота поперечного сечения образца, м.
Площадь основного поперечного сечения образца без учёта арматуры, м2,
54
A1 A A2 , |
(2.2) |
где A2 – площадь поперечного сечения арматуры, м2, определяемая по формуле |
|
A2 2 2b2, |
(2.3) |
где b2 – ширина поперечного сечения арматуры, м; 2 – высота поперечного сечения арматуры, м.
При действии нагрузки балка испытывает две стадии напряжённого состояния.
Первая стадия продолжается от момента нагружения до момента образования первой трещины, нормальной к его продольной оси. Первая трещина образуется в опасном сечении под нагрузкой при достижении растягивающими напряжениями значений, равных рас-
чётному сопротивлению льда на растяжение ( 0 |
= Rраст). Рассмотрим |
|||
данную стадию более подробно. |
|
И |
||
|
|
|
||
Определим положение нейтральной оси Z0 |
поперечного сечения |
|||
армированного образца. |
|
Д |
|
|
|
|
|
|
|
Статический момент сечения льда (S1) и арматуры (S2) относи- |
||||
тельно нейтральной оси |
А |
|
|
|
|
|
|
|
|
S1 |
A1 y1 , |
|
(2.4) |
|
б |
до оси Z1, м. |
|
||
где y1 – расстояние от нейтральной оси Z0 |
|
|||
S2 |
A2 y2 , |
|
(2.5) |
|
где y2 – расстояние от нейтральной оси Z0 до центра тяжести поперечного сечения арматуры, м.
|
|
|
|
|
h |
|
|
|
|
|
|
y |
2 |
|
a y1 y0 , |
(2.6) |
|||||
|
2 |
|||||||||
где a – расстояние от центраитяжести поперечного сечения арматуры до нижней |
||||||||||
грани образца, м. |
|
|
|
|
|
|
|
|
|
|
С |
|
|
|
|
A |
h |
|
|
||
y |
0 |
|
|
2 |
|
|
a |
(2.7) |
||
|
A |
|
||||||||
|
|
|
2 |
. |
||||||
|
|
|
|
|
1 |
|
|
|
|
|
Если учесть, что dA dA dA 0, |
тогда стати- |
|||||||||
|
|
|
|
|
|
|
Aсж |
Aраст |
|
|
ческий момент армированного сечения относительно нейтральной оси должен быть равен нулю:
SZ0 |
0. |
(2.8) |
Армирование делает рассматриваемое сечение неоднородным. Для решения задачи приведём его к однородному виду, тогда нулю должен быть равен приведённый статический момент Sприв:
55
S |
|
A y A y |
|
E2 |
0, |
|
прив |
2 E |
|||||
|
1 1 2 |
|
||||
|
|
|
1 |
|
||
где E1 – модуль упругости льда, МПа; E2 – модуль упругости арматуры, МПа.
С учётом (2.7) и (2.8) получаем
|
|
|
E |
2 |
|
|
h |
|
|
|
|
|
A |
2 |
|
|
||
|
A |
|
|
|
|
|
a |
|
1 |
|
|
|
||||||
2 E |
|
2 |
A |
|
||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
||||||||
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
. |
(2.9) |
|
|
|
|
|
A A |
|
|
E2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
2 |
|
E1 |
|
|
|
|
|
|||
Момент инерции J основной части сечения без учёта арматуры относительно оси Z
|
|
|
|
|
J |
|
|
bh3 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
(2.10) |
|||
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Момент инерции J2 сечения арматуры относительно нейтраль- |
|||||||||||||||||||||
ной оси Z0 |
|
|
|
|
|
|
|
|
|
|
Д |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.И |
|
|||
|
J |
b2 |
23 |
|
|
A y2 |
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
А |
|
|
|
|
|
(2.11) |
|||||||||||
|
|
2 |
|
|
6 |
|
|
|
|
2 |
|
2 |
|
|
|
||||||
Момент инерции J1 |
б |
|
|
|
|
|
относительнонейтральной оси Z0 |
||||||||||||||
площади |
|
1 |
|
||||||||||||||||||
|
J 1 |
|
J Ay42 J2. |
(2.12) |
|||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Модуль упругости |
момент инерции приведённого сечения: |
||||||||||||||||||||
С |
E |
|
|
E |
|
|
|
|
J1 |
E |
|
J2 |
, |
(2.13) |
|||||||
|
|
пр в |
|
1 |
|
J |
|
|
2 |
J |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
J |
прив |
J |
1 |
|
E2 |
|
J |
2 |
, |
|
|
(2.14) |
||||||||
|
E1 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
EпривJ E1Jприв.
Определяем напряжения, возникающие во льду и арматуре. Напряжения в основной части поперечного сечения, состоящей
изо льда,
|
|
|
E1 |
|
M |
y , |
(2.15) |
|
Eприв |
|
|||||
|
1 |
|
|
J 1 |
|||
где М – изгибающий момент в опасном сечении ( h2 y h1).
M |
Fl |
, |
(2.16) |
|
|||
4 |
|
|
|
где F – сила, действующая на образец, кН; l – расстояние между опорами, м.
56
Напряжения в арматуре |
|
E2 |
|
M |
|
|
|
2 |
|
|
y2. |
(2.17) |
|||
Eприв |
|
||||||
|
|
|
J |
|
|||
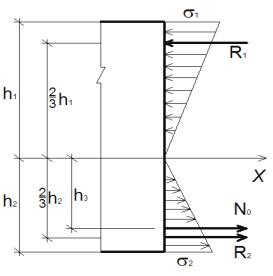
Определим равнодействующие внутренних сил (рис. 2.11), возникающих в растянутой и сжатой зонах поперечного сечения (R2 и R1):
R1 |
|
1 |
1h1 b, |
(2.18) |
|
||||
|
2 |
|
|
|
R |
|
1 |
h |
b. |
(2.19) |
|
|
||||||
2 |
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
Д |
|
|
|
|
|
А |
|
|
Р с. 2.11. Расчётная схема для определения |
|
||||
|
R1б, R0 N0 в первой стадии |
|
|||
Растягивающее |
|
в арматуре N0 |
определяем из условия |
||
усилие |
|
|
|
||
X N0 R1 |
R2 |
0 N0 |
R1 R2 . |
(2.20) |
|
С |
|
|
|
|
|
Первая стадия напряжённо-деформированного состояния балки завершается в момент появления в ней поперечной трещины. При проведении лабораторных испытаний образование первой трещины, нормальной к продольной оси балки, происходило при достижении нагрузки от 3,8 до 7 кН, т.е. при достижении предела прочности Rизг, равного0,4÷0,8 МПа (еговеличина зависит от физических свойств льда).
Построив график (рис. 2.12) зависимости растягивающих напряжений от приложенной нагрузки (на основании известных теоретических данных), мы получили значения, которые соответствуют данным, полученным в ходе лабораторных исследований.
57

|
|
|
|
|
|
И |
Рис. 2.12. Зависимость растягивающих напряжений от |
||||||
|
|
приложенной нагрузки |
||||
|
|
|
|
Д |
||
Исследования армированных и неармированных образцов льда |
||||||
(рис. 2.13) показали различия в их работе. |
|
|||||
а |
|
|
А |
б |
|
|
|
|
б |
|
|
|
|
|
и |
|
|
|
|
|
|
С |
|
|
|
|
|
|
Рис. 2.13. Разрушение неармированного (а) |
|||||
и армированного (б) образцов
При достижении предела прочности ( 1 = Rизг) в балке появляется поперечная трещина. При этом неармированный образец разрушается, образуя две призматические части. Если же образец армирован, то после появления первой трещины он не разрушается, а переходит на вторую стадию. При этом происходит скачкообразное падение нагрузки, а затем плавный её рост (рис. 2.14), чередующийся с последующими скачками падения, являющимися результатом продолжающегося трещинообразования и постепенного разрушения арматуры.
58

Длительность работы образца во второй стадииИ(до момента полного разрушения) зависит от прочности и деформативности армирующего
Рис. 2.14. Диаграмма, иллюстрирующая характер разрушения армированных и неармированных балок изо льда:
1 – неармированный образец; 2 – армированный образец
Во второй стадии в работу вступает армирующий материал.
честву). При этом образованбе новых трещин в балке происходит при более высоких напряжен ях в арматуре. С ростом деформаций в рас-
материала и силы сцепления между армирующим и армируемым ма- |
|
териалами. |
Д |
|
|
Вторая стадия характеризуется дальнейшим развитием трещи- |
|
|
А |
нообразования (как по вел ч не раскрытия трещин, так и по их коли- |
|
тянутой зоне иСв арматуреипроисходит увеличение напряжений, как в ледовом массиве, так и в армирующем геосинтетическом материале. При этом растягивающие напряжения во льду достигают предельных значений раньше, чем в армирующем материале.
В конце второй стадии ширина раскрытия трещин и прогиб балки становятся настолько большими, что конструкция не способна воспринимать дополнительную нагрузку.
Конец второй стадии характеризуется нарушением сплошности льда. Лёд начинает работать как дискретный материал, что приводит к разрушению образца без разрушения арматуры (см. рис. 2.13, б).
После образования трещины (вторая стадия) расчётная схема и схема действия сил показаны на рис. 2.15.
59
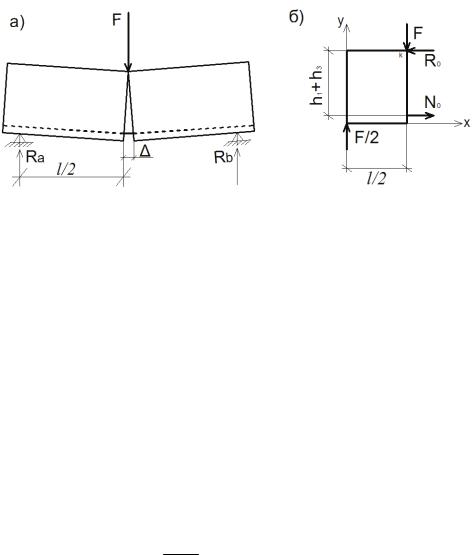
Рис. 2.15. Расчётная схема работы балки (а) и схема действия сил (б) на фрагмент балки во второй стадии
Растягивающее усилие в арматуре (N0) находим из условия рав-
новесия фрагмента балки ( Mk |
0): |
И |
|
|||
N0 |
Fl |
|
|
. |
(2.21) |
|
|
|
|
||||
4 h h |
|
|
||||
|
2 |
3 |
|
Д |
|
|
|
1 |
|
|
|
|
|
Для оценки состояния образца на второй стадии используем мо- |
||||||
дель плоского напряжённого состояния. Напряжение определяем при помощи функции напряжений Эри (x, y) [86]:
x |
|
|
, |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
y2 |
|
|
|
|
|||||||||
|
|
|
|
|
А |
|
|
|
|||||
|
|
2 |
|
|
|
||||||||
y |
|
б2 , |
|
|
|
|
|
||||||
|
|
x |
|
|
|
|
|
|
|
(2.22) |
|||
и |
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
||||||||
xy |
|
|
|
|
Xy Yx, |
|
|||||||
|
|
|
|
||||||||||
|
|
|
|
x y |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где X, Y – постоянные объёмные силы. |
|
|
|
|
|
|
|||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение плоской задачи заключается в определении функции |
|||||||||||||
напряжений (x, y) из бигармонического уравнения (2.22): |
|
||||||||||||
|
4 |
|
|
|
4 |
|
4 |
|
|
|
|||
|
|
2 |
|
|
|
|
|
0. |
(2.23) |
||||
|
4 |
2 |
2 |
4 |
|
||||||||
|
x |
|
x |
y |
y |
|
|
|
|||||
Используя метод конечных разностей [87], исследуемую плоскость разобьём на сетку с прямоугольными ячейками размерами x иy. Для упрощения расчётов сетку выберем с квадратными ячейками:
60

x= y=γ. Бигармоническое уравнение в конечных разностях, записанное для произвольной точки (рис. 2.16), имеет вид
20 0 8( 1 2 3 4) 2 6 8 10 12 5 7 9 11 0.(2.24)
Уравнение (2.23) связывает между собой значения функции в тринадцати точках разностной сетки (см. рис. 2.16).
Напряжения в точке 0 без учёта объёмных сил
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x 0 |
|
|
|
|
2 |
2 0 4 , |
|
|
|
|
|
|||||||||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|||||||||||||||||||
|
y |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
|
|
|
, |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
3 |
|
|
|
|
|
|||||||||||
|
|
2 |
|
|
2 |
|
|
|
|
|||||||||||||||||||
|
|
y 0 |
|
|
x |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
(2.25) |
|||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
6 |
|
8 |
|
10 |
|
. |
|
||||||||||||
|
xy 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
||||||||
|
|
|
|
|
x y |
0 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|||||||||||||
Уравнения |
|
вида |
(2.24) |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
можно составить для каждого |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
из узлов внутри конура. При |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
этом в часть уравнений вой- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
дут и значения функций для |
А |
|
|
|
|
|
|
|
|
|||||||||||||||||||
узлов на контуре и для узлов, |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|||||||||||||
расположенных на расстоян |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
одного шага вне контура. На |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
рис. 2.16 внеконтурная сетка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
показана штрихами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Значения функции на |
|
|
Рис. 2.16. Область, разбитая на ячейки |
|||||||||||||||||||||||||
контуре и вне контура находят |
|
|
||||||||||||||||||||||||||
из граничных условий. Таким образом, неизвестных значений функции окажется столько, сколько узлов внутри контура, но столько же можно составить уравнений вида (2.25).
Значения функции на контуре и вне его найдём из предположения А.П. Синицына о том, что значение на контуре исследуемой области принимается равным значениям изгибающего момента в балке с такой же нагрузкой, что и на краю данной области.
Если на верхней грани прямоугольной области приложена нагрузка q (x), направленная вниз, то для этой грани можно составить следующее условие:
61
y |
|
2 |
q. |
(2.26) |
|
x |
2 |
||||
|
|
|
|
|
|
Сравнивая это соотношение с зависимостью между изгибающим моментом и интенсивностью распределённой нагрузки при изгибе ба-
лок |
d2M |
q, |
заключаем, что функцию напряжений на контуре |
|
dx |
2 |
|||
|
|
|
|
|
пластинки можно принять за значение изгибающего момента в данной точке для балки с такой же нагрузкой. При этом закрепления балки можно принимать любые, так как крепление оказывает влияние только на значения постоянных, появляющихся после интегрирования соотношения (2.26):
M C1x C2 . |
(2.27) |
ным знаком. Производные от функции наИверхней и нижней гранях
На величину напряжений закрепления балки влияния не окажут,
так как напряжение y равно второй части производной функции по x и постоянные С1 и С2 исчезают. На нижней грани пластинки функцию следует брать равной значению изгибающего момента с обрат-
|
|
, а на боковых гранях |
|
|
|
представляют собой поперечные силы в |
|||||
|
x |
|
y |
||||||||
|
|
|
|
|
Д |
|
|||||
соответствующих точках |
|
алки. |
|
|
|
|
|||||
|
|
Производные на верхней, нижней и на боковых гранях можно |
|||||||||
найти из формулы |
|
|
|
|
А |
|
|||||
|
б |
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
и |
xy |
|
. |
(2.28) |
||||
|
|
|
|
||||||||
|
|
|
|
|
x y |
|
|||||
|
|
Значения производных в точках контура можно использовать и |
|||||||||
для определенияСзначений функции в точках вне контура. Так, для точки b (см. рис. 2.16) можно составить следующее соотношение:
|
|
|
|
|
1 |
|
|
|
|
. |
|
|||
|
|
|
|
a |
|
c |
(2.29) |
|||||||
|
|
|||||||||||||
|
y |
|
|
|
2 |
|
|
|
|
|
||||
|
b |
|
|
|
|
|
|
|
|
|
|
|||
Из выражения (2.29) находим значение функции в точке a, |
||||||||||||||
расположенной вне контура пластинки: |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
a |
|
c |
2 |
|
|
. |
(2.30) |
||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
y b |
|
|||
Точно так же для точки l, лежащей на боковой грани:
62

|
|
|
1 |
m |
k . |
|
|
|
|
|
|
(2.31) |
|||
|
2 |
||||||
|
x l |
|
|
|
|
||
Из выражения (2.31) находим значение функции в точке k, лежащей вне контура пластинки:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
k |
m 2 |
|
|
|
|
. |
|
(2.32) |
||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
x l |
|
|||||
В результате плоская задача |
|
|
|
|
|
|
|
|
|
|
||||||
сводится к определению функции |
|
|
|
|
|
|
|
|
|
|
||||||
(x, y) во всех узлах сетки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для решения задачи иссле- |
|
|
|
|
|
И |
|
|||||||||
дуемая нами область была разбита |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
на ячейки (рис. 2.17) размерами |
|
|
|
|
|
|
|
|
|
|
||||||
x= y=1 см. В результате мы по- |
|
|
|
|
|
|
|
|
|
|
||||||
лучили 14 узлов по оси У и 11 уз- |
|
|
|
|
|
|
|
|
|
|
|
|||||
лов по оси X. |
|
|
|
А |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В результате расчётов были |
|
|
|
|
|
|
|
|
|
|
||||||
вычислены нормальные напряже- |
|
|
|
|
2 |
|
|
|||||||||
|
|
б |
|
|
|
|
|
|
|
|||||||
ния x, y, касательные xy |
и глав- |
Д |
|
|||||||||||||
ные напряжения max и min, кото- |
Рис. 2.17 |
Конечно-разностная дискре- |
||||||||||||||
тизация фрагмента исследуемой балки |
||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
||||
рые были определены по формуле |
|
|
|
|
|
|
|
|
|
|
|
|||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
y |
|
x |
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
y |
|
|
||||||
max,min |
|
|
|
|
|
|
|
|
|
|
|
|
xy . |
(2.33) |
||
|
|
2 |
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
По результатам расчёта построены эпюры напряжений (рис. 2.18 – 2.22).
Угол наклона нормали главной площадки определяется по выражению
tg2 0 |
|
2 xy |
|
. |
(2.34) |
|
|
x |
|
|
|||
|
|
|
y |
|
||
Если угол имеет положительное значение, то он откладывается против часовой стрелки, если угол имеет знак минус, то по часовой стрелке.
63

|
|
|
|
И |
Рис. 2.18. Эпюра нормальных напряжений x |
||||
|
|
|
Д |
|
|
|
А |
|
|
|
б |
|
|
|
и |
|
|
|
|
С |
|
|
|
|
Рис. 2.19. Эпюра нормальных напряжений y
64

|
|
|
|
И |
Рис. 2.20. Эпюра касательных напряжений xy |
||||
|
|
|
Д |
|
|
|
А |
|
|
|
б |
|
|
|
и |
|
|
|
|
С |
|
|
|
|
Рис. 2.21. Эпюра главных максимальных напряжений max
65

|
|
|
|
И |
Рис. 2.22. Эпюра главных минимальных напряжений min |
||||
|
|
|
Д |
|
По результатам вычислений были построены изолинии действия |
||||
главных напряжений (рис. 2.23). |
|
|
||
|
|
А |
|
|
|
б |
|
|
|
и |
|
|
|
|
С |
|
|
|
|
Рис. 2.23. Изолинии действия главных напряжений
Сравнивая полученные изолинии с трещинами, образующимися в образцах при проведении лабораторных испытаний (см. рис. 2.13, б), можем сделать заключение, что наклон и зона локализации трещин достаточно хорошо совпадают с аналогичными характеристиками изолиний. Это подтверждает адекватность выбранной модели армированного образца [88].
66
