Принципы выбора оценок погрешностей

В целях единообразия представления результатов и погрешностей измерений показатели точности и формы представления результатов измерений стандартизованы. Стандартом установлено, что в численных показателях точности измерений (в том числе и в погрешностях) должно быть не более двух значащих цифр. При записи результатов измерений наименьшие разряды числовых значений результата измерения и численных показателей точности должны быть одинаковыми. Расчет погрешности округления показывает, что при округлении до двух значащих цифр она составляет не более 5%, а при округлении до одной значащей цифры - не более 50%.

6.3. Систематическая составляющая погрешности

Источниками систематических составляющих погрешностей измерения ("систематических эффектов") могут быть все его компоненты - неадекватная модель объекта измерения, метод измерения, средства измерений и оператор. Оценивание систематических составляющих представляет довольно трудную метрологическую задачу. Трудность заключается в сложности обнаружения систематической погрешности, так как чаще всего ее невозможно выявить путём повторных измерений. Единых рекомендаций по обнаружению и оцениванию методических составляющих систематической погрешности нет. В каждом конкретном случае задача решается индивидуально.

Постоянные инструментальные систематические погрешности выявляют посредством поверки. Поправкачисленно равна выявленному значению систематической погрешности и противоположна ей по знаку. Исправленный результат измерения получают алгебраическим суммированием результата наблюдения и поправки.

Личные систематические погрешности связаны с индивидуальными особенностями оператора. При проектировании средств измерения стремятся максимально исключить возможность появления личных погрешностей. Кроме того, для устранения личных погрешностей необходимо точно соблюдать правила эксплуатации средств измерений и иметь соответствующую квалификацию.

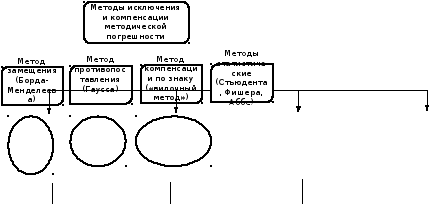
В практике измерений применяют ряд приемов (методов), позволяющих получить результат измерения свободным или почти свободным от постоянной систематической погрешности. К таким приемам относят метод замещения, метод противопоставления, метод компенсации по знаку и другие.

Методы устранения систематических погрешностей

6.4. Случайная составляющая погрешности

Когда при проведении с одинаковой тщательностью и в одинаковых условиях повторных наблюдений одной и той же постоянной величины получают результаты, отличающиеся друг от друга, это свидетельствует о наличии в них случайных погрешностей ("случайных эффектов"). Каждая такая погрешность возникает вследствие одновременного воздействия на результат наблюдения многих непредсказуемых возмущений, и сама является случайной величиной. Методы теории вероятностей и математической статистики позволяют установить вероятностные (статистические) закономерности появления случайных погрешностей и на основе этих закономерностей дать количественные оценки результата измерений и случайной составляющей его погрешности.

Свойства случайной величины описывается функцией распределенияF(x), которая определяет вероятность того, что случайная величинаx будет меньшеx₁:

F(x) = P{x < x₁}. Функция распределения – неубывающая функция, определённая так, чтоF(-)= 0иF(+)= 1. Наряду с функцией распределенияF(x), называемойинтегральной иликумулятивной, широко применяютдифференциальную функцию f(x), которую обычно называютплотностью распределения вероятностей:

.

Функция f(x) всегда неотрицательна и подчиненаусловию нормированияв виде

Это означает, что площадь под графиком кривой f(x) всегда равна единице.

В метрологической практике чаще всего имеют дело с нормальным и с равномерным законами распределения погрешностей. В нормативной метрологической документации в качестве модели распределения случайной составляющей погрешности принимается нормальное распределение, а модели неисключенной систематической составляющей - равномерное распределение.

Для нормального распределения имеем:

;.

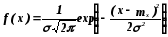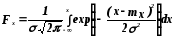Здесь: параметр D = ² - дисперсия, - среднее квадратичное отклонение,m_x - математическое ожидание случайной величины (истинное значение измеряемой величины при отсутствии систематических погрешностей).

В измерительном эксперименте для выборки (группы из nнаблюдений) случайных величинx_i, распределенных по нормальному закону, аналогами теоретических параметровm_xиявляютсясреднее арифметическое выборки (координата центра распределения)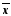исреднее квадратичное отклонение выборки(по международной терминологии –стандартное отклонение)S(x):

; .

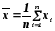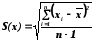Вычисление F(x)при некотором фиксированномx₁даёт вероятностьP{x < x₁} = P₁. При использовании графикаf(x) для вычисления этой величины нужно найти площадь под кривой, расположенную левее точкиx₁(рис. 6.1).

Рис. 6.1. Интегральная (а) и дифференциальная (б) функции распределения случайной величины

В расчётах широко применяют центральное нормированное нормальное распределение, которое получается при переходе к случайной величине:

;

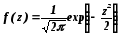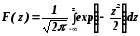
В научной и технической литературе часто приводят таблицы значений функции Ф(z), называемой функцией Лапласа и определяемой выражением:

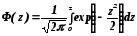
Очевидно, что для z  0 F(z)= 0.5 + Ф(z). Параметры ветви дляz < 0 находят на основе симметрии: F(z)= 0.5 − Ф(z). Дляравномерного закона распределенияслучайной величины:

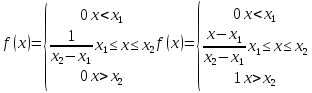
Для количественной оценки случайных погрешностей и установления границ результата измерения используют различные варианты: предельная погрешность, интервальная оценка, числовые характеристики закона распределения.

Предельная погрешность _m -погрешность, больше которой в данном измерительном эксперименте не может появиться. Такая оценка погрешности правомерна только для равномерного распределения, где границы чётко выражены и существует такое значение_m, которое ограничивает возможные значения случайных погрешностей с обеих сторон отцентра распределения.

Более универсальной и информативной является квантильная оценка. Площадь под кривой плотности распределения погрешностей делят вертикальными линиями на части. Абсциссы таких линий называютквантилями. Квантильная оценка погрешности представляется интервалами от −x(P) до+x(P), на которых с заданной вероятностьюPвстречаютсяP · 100% всех возможных значений случайной погрешности.

Интервал с границами x(P) называютдоверительным интервалом случайной погрешности, а соответствующую ему вероятностьP_Д–доверительной вероятностью. При оценке случайной погрешности доверительными границами необходимо указывать значение принятой доверительной вероятности (например,0,5 В приP_Д = 0,95). Доверительные границы случайной погрешностиx(P), соответствующие доверительной вероятностиP_Д, находят по формуле:

x(P) = t·,

где t- коэффициент, зависящий отP_Ди вида закона распределения.

На графике нормального распределения погрешностей по оси абсцисс отложены интервалы с границами ; 2;3(рис. 6.2).

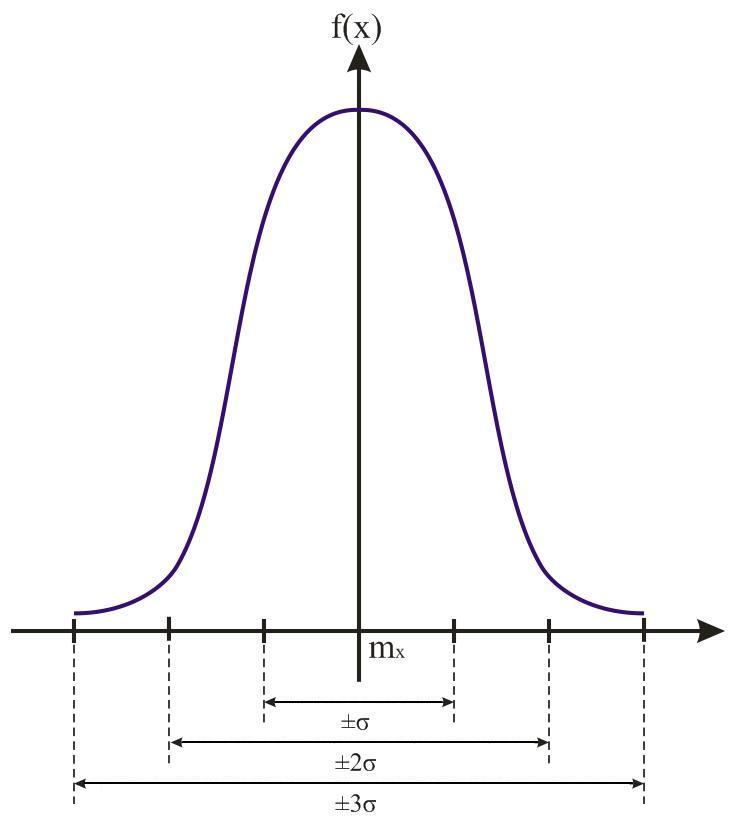
Рис. 6.2. Оценка границ доверительного интервала

Для достоверной оценки границ доверительного интервала необходимо, чтобы число наблюдений n было не меньшим, чемn  (1 + P_Д) / (1 − P_Д). При нормальном распределении погрешностей принято считать случайную погрешность с границами3 предельной (максимально вероятной) погрешностью. В этом случае нормальное распределение называютусеченным. Использование усеченного нормального закона распределения характерно для механических измерений.

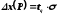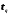Для оценки границ доверительного интервала при малом числе измерений (n  30) одной и той же величины используют формулу,где- коэффициент Стьюдента, зависящий от значения доверительной вероятности и числа измеренийn. При увеличении числа измерений распределение Стьюдента приближается к нормальному распределению.