7.3. Косвенное измерение

При косвенных измерениях искомое значение величины A находят расчётом на основе прямых измерений других величин, связанных с измеряемой величиной известной зависимостью:

A = f (a₁, a₂, … a_i,… a_m) (7.5)

Результатом косвенного измерения является оценка величины А, которую находят подстановкой в формулу (7.5) оценок аргументовa_i. Поскольку каждый из аргументовa_iизмеряется с некоторой погрешностью, то задача оценивания погрешности результата сводится к суммированию погрешностей измерения аргументов. Вклад отдельных погрешностей измерения аргументов в погрешность результата зависит от вида функции (7.5).

С точки зрения оценки погрешностей косвенные измерения делят на линейные и нелинейные. При линейных косвенных измерениях уравнение измерений имеет вид:

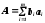
где b_i – постоянный коэффициент при аргументеa_i. Любые другие виды функциональной зависимости (7.5) относят к нелинейным косвенным измерениям.

Погрешности измерения аргументов могут быть заданы либо своими грани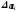цами , либо доверительными границами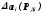с доверительными вероятностями.

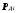Простейшая оценка погрешности результата 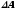получается суммированием предельных погрешностей, т.е. подстановкой границa₁, a₂, … a_mв выражение:

A = a₁ + a₂ + … + a_m(7.6)

Такая оценка завышена, так как предполагает, что погрешности аргументов одновременно максимальны и имеют один знак. Более корректно статистическое оценивание:

.

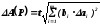Если погрешности измерения аргументов заданы доверительными границами с одинаковыми доверительными вероятностями P_Д, то при нормальном распределении этих погрешностей доверительные границы результата находят по формуле:

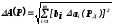(7.7)

Нелинейные косвенные измерения характерны тем, что результаты измерений аргументов подвергаются функциональным преобразованиям. Поэтому при нелинейных косвенных измерениях отказываются от интервальных оценок погрешности результата, ограничиваясь приближённой оценкой её границ. В основе приближённого оценивания погрешности нелинейных косвенных измерений лежит линеаризация функции (7.5) и дальнейшая обработка проводится как при линейных измерениях

Из выражения для полного дифференциала функции А, заменяя дифференциалы на погрешности, получаем:

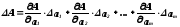(7.8)

Для случая равномерного распределения погрешностей аргументов при числе слагаемых m < 5 границы погрешностей определяют по формуле (7.6). Если погрешности аргументов заданы их доверительными границами, оценку погрешности результата измерения выполняют по (7.7). При этом роль коэффициентовb₁, b₂, …, b_mвыполняют частные производные:

.

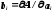Для наиболее часто встречающихся функциональных зависимостей формула (7.8) даёт простые правила оценивания абсолютной Aили относительнойAпогрешностей косвенного измерения.

7.4. Совместное измерение

Этот вид измерений характерен тем, что его целью является установление функциональной зависимости между двумя величинами. Для отыскания зависимости y = f(x) между переменными последовательно устанавливают и измеряют значенияx, одновременно измеряя значенияy. В результате измерений получают координаты исследуемой зависимости (x_i, y_i). Так как результаты измеренияxиyсодержат погрешности, полученные координаты не будут принадлежать истинной зависимости. Поэтому при выполнении совместных измерений, возникает задача аппроксимации зависимостиy = f(x) по экспериментальным данным так, чтобы она наилучшим образом описывала истинную зависимость. Кроме того, необходимо ответить на следующие вопросы:

1. действительно ли аппроксимирующая функция наилучшим образом приближается к искомой зависимости;

2. какой мерой можно оценить приближение экспериментальной зависимости к истинной.

Подобные задачи решаются с применением метода наименьших квадратов. В этом методе оценки параметров зависимости определяют из условия, что сумма квадратов отклонений расчетных значений аппроксимирующей функции от экспериментальных значений должна быть минимальна. При этом предполагается, что результаты измерений (x_i, y_i),i = 1, 2, … mудовлетворяют следующим условиям:

0. - значения аргумента x_iизвестны точно;

1. - систематические погрешности исключены, и результаты измерений y_iсодержат лишь случайные погрешности, которые независимы и имеют одинаковые дисперсии;

2. - погрешности измерения y_iимеют нормальное распределение.

На практике часто встречается случай построения методом наименьших квадратов линейной зависимости y = A + Bx, гдеAиB– постоянные. График функции – прямая линия с углом наклоном = arctg B, пересекающая ось ординат в точке с координатойA.

Каждая экспериментальная точка попадает в поле прямоугольника со сторонами 2x,2y. В случае малых погрешностей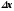экспериментальные точки будут иметь отклонения от идеальной прямой только в пределах погрешности измеренияy_i.

Задача определения наилучшей прямой, аппроксимирующей набор из mэкспериментальных точек (x₁, y₁), … (x_m, y_m) сводится к отысканию значений постоянныхАиВ.

В теории метода наименьших квадратов показано, что наилучшие значения для постоянных АиВ – это те, для которых имеет место минимальное значение выражения:

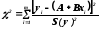(7.9)

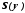Здесь - стандартное отклонение погрешности измеренияy.

Продифференцировав (7.9) по Аи поВи приравняв производные нулю, получим систему уравнений для определения искомых постоянных:

;

,

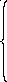
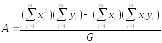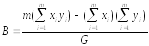Здесь .

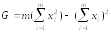Представление о приближении аппроксимирующей функции к истинной зависимости получим, оценив погрешности в определении постоянных АиВ. ПогрешностиΔАиΔВнаходят расчетом по правилам косвенных измерений, исходя из погрешностей измеренияΔy₁, … Δy_m.

Стандартные отклонения погрешностей S(y),S(A) иS(B) можно вычислить по формулам:

;

;

.

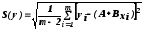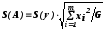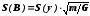Метод наименьших квадратов используется для решения задач аппроксимации многих зависимостей, в том числе выражаемых:

- полиномами y = A + Bx + Cx²+ +…+ Hx^m ;

- экспоненциальными функциями y = A exp(Bx),

где А, В, С,…,Н– постоянные коэффициенты.