
2336
.pdf
М1 14,3 Н·м и М2 62,4 Н·м соответственно. Диаметры начальных окружностей d1 36,36 мм, d2 163,64 мм.
Находим силы, действующие в зубчатой передаче:
– окружная сила
F 2M |
1 |
/d 2 14,3 103 /36,36 786,6 Н, |
|
t |
|
1 |
|
– радиальная сила |
|
|
|
F F tg /cos 786,6 tg200 /cos804' 289 Н, |
|||
r |
t |
|
|
– осевая сила |
|
|
|
|
F F tg 786,6 tg804' 111,5 Н. |
||
|
a |
|
t |
Силы в зацеплении, приложенные к шестерне и к колесу, равны между |
|||
собой, т.е. Ft1 Ft2 |
Ft , |
Fr1 Fr2 Fr и Fa1 Fa2 Fa . Поэтому силы, |
|
приложенные к валу шестерни, равны силам, приложенным к валу колеса. Окружная и радиальная силы действуют перпендикулярно к оси вала,
поэтому сложим их геометрически:
F1 
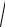 Ft2 Fr2
Ft2 Fr2 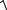
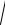 786,62 2892 838 Н.
786,62 2892 838 Н.
Поскольку редуктор одноступенчатый, то подшипники расположены симметрично относительно зубчатых колес и реакция каждой опоры будет равна половине F1 – суммарной радиальной силы, т.е.
R1 R2 R 0,5F1 0,5 838 419 Н.
Осевая нагрузка на подшипник
A Fa 111,5 Н.
По формуле (4.3) из т. 3 определяем необходимую динамическую грузоподъемность подшипника, нагруженного радиальной R и осевой A си-
лами (т.3, рис. 4.1, б):
C (R кК mA)кБ кТ (6 10 5nh)1/ ,
где кК 1 – кинематический коэффициент (т. 3, табл. 4.2); кБ 1,2 – коэффициент безопасности (см. т. 3, табл. 4.1); кТ 1 – температурный коэффициент (т. 3, табл. 4.3); А/ R 111,5/419 0,266; m 1,5 – коэффициент осевой нагрузки (т. 3, табл. 4.4); 3 – показатель степени для шариковых подшипников. С учетом подстановок, выбора срока службы h 10000 ч. и числовых вычислений формула (4.3) из т. 3 примет вид
51
C (R mA) n0,33. |
(2.38) |
После подстановки числовых значений для вала I получим
С1 (419 1,5 111,5) 14250,33 6440 Н 6,44 кН.
Подставляя числовые значения для вала II, получим
С2 (419 1,5 111,5) 3160,33 3915 Н 3,9 кН.
Сравниваем расчетные данные с каталожными (см. т. 3, табл.4.1):
– первый вал
С1расч 6,44 кН С1табл 14 кН,
– второй вал
С2расч 3,9 кН С2табл 25,5 кН.
Расчет следует считать удовлетворительным.
Теперь из таб. 4.1, т. 3, выбираем размеры подшипников:
– |
подшипник 205: |
d1 25 |
мм, D1 52 |
мм, В1 15 мм; |
– |
подшипник 207: |
d2 35 |
мм, D2 72 |
мм, В2 17 мм. |
17.8. После расчетов на компоновочном чертеже (см. т. 3, рис. 4.3) проводим осевыми линиями, параллельными торцам зубчатых колес, на расстоянии с от них по обе стороны колес оси симметрии подшипников. Вычерчиваем подшипники по размерам, взятым из табл. 4.1, т. 3, согласно рис. 4.4, т. 3.
Диаметр шарика определяется по формуле (4.5) из т. 3:
–для подшипника №205
Н1 (D1 d1)/2 (52 25)/2 13,5 мм,
dК1 0,64Н1 0,64 13,5 8,64 9 мм;
–для подшипника №207
Н2 (D2 d2)/2 (72 35)/2 18,5 мм,
dК2 0,64Н2 0,64 18,5 11,84 12 мм.
Толщина колец:
– для подшипника №205
h1 0,3H1 0,3 13,5 4 мм;
– для подшипника №207
h2 0,3H2 0,3 18,5 5,5 мм.
52
17.9. Шестерню изготовляют обычно заодно с валом. Такая деталь называется “вал-шестерня”. По обе стороны шестерни сделаны бурты. Буртом называется утолщенная часть вала, предназначенная для того, чтобы в нее упиралась своим торцом какая-либо деталь. В нашем случае это подшипник, который упирается торцом своего внутреннего кольца в бурт вала. Диаметр бурта dБ больше диаметра шейки под подшипник dП на величину двух заплечиков tБ (т. 3, табл. 4.7).
Определяем диаметр буртов dБ1 (dБ3) вала-шестерни по обе стороны от шестерни по формуле (4.6), рис. 4.3 (т. 3),
dБ1 dП1 2tБ 25 2 4,5 34 мм.
Согласно ряду (4.8) Ra 40 (т. 3) выбираем dБ1 34 мм.
На чертеже согласно рис. 4.3 (т. 3) проводим слева и справа от шестерни контуры буртов до подшипников.
17.10. Находим диаметр отверстия в зубчатом колесе и соответствующей ему шейки вала dШ2 (dШ4) по формуле (4.7) из т. 3:
dШ2 dП2 2...4 35 2 37 мм 38 мм.
Выбираем согласно ряду Ra 40 диаметр dШ2 38 мм, хотя для диаметров посадочных мест желательно применять ряд Ra 20, но в формуле (4.7 из т. 3) 2 мм соответствуют малым диаметрам, а 4 мм – большим.
17.11. По формулам (4.9) и (4.10) из т. 3 находим диаметр dС и длину lС ступицы колеса
dС 1,8dШ2 1,8 38 68,4 мм.
lС (1,2...1,5)dШ2 1,5 38 57 мм.
Для несопрягаемых размеров согласно ряду Ra 40 назначаем dС 75
мм и lС 60 мм.
На чертеже вычерчиваем контуры ступицы и посадочную шейку вала диаметром dШ2. Эта шейка простирается от левого торца ступицы (бурта вала) до торца правого подшипника (см. т. 3, рис. 4.3).
17.12. Левый торец ступицы колеса упирается в бурт вала II (IV), диаметр которого dБ2 (dБ4). Слева в этот бурт упирается левый подшипник. Диаметр бурта dБ2 (dБ4) определяется по формуле (4.6) из т. 3:
dБ2 dП2 2tБ 35 2 4,5 44 мм 45 мм.
Выбираем согласно ряду Ra 40 dБ2 45 мм. Делаем проверку по формуле (4.11) из т. 3:
53
dВК dП2 0,6Н2 35 |
0,6 18,5 46 мм. |
dВК 46 мм >d |
Б2 45 мм, |
что удовлетворительно.
Между правым торцем левого подшипника вала II (IV) и левым торцом ступицы колеса вычерчиваем шейку бурта диаметром dБ2 (dБ4).
Между правым торцом ступицы колеса и левым торцом правого подшипника устанавливаем дистанционное кольцо, у которого внутренний диаметр равен диаметру шейки вала dШ2, а наружный диаметр – dБ2.
17.13. Определяем диаметры шеек под уплотнение подшипников по формуле (4.12) из т.3:
– на 1-м валу (t3 – по табл. 4.7, т. 3)
dУ1 dВ1 2t3 16 2 3,5 23 мм 24 мм,
выбираем манжету по рис. 4.5 и табл. 4.2 (т. 3) с внутренним отверстием dУ1 24 мм, DУ1 40 мм, BУ1 10 мм;
– на 2-м валу
dУ2 dВ2 2t3 25 2 4,5 34 мм 35 мм,
выбираем манжету с внутренним отверстием dУ2 35 мм, DУ2 58 мм,
BУ2 10 мм.
Вычерчиваем шейки валов под уплотнение, у которых длина шейки равна диаметру согласно формуле (4.13) из т. 3, т.е.
lУi dУi .
Выбираем (т. 3, рис. 4.5) 2 5 мм, tУ 3 мм, 30o .
17.14. Определяем длину входной и выходной шеек валов диаметрами dВ1 и dВ2 по формуле (4.14) из т. 3:
– для входного вала I (III)
lВ1 1,8 dВ1 1,8 16 28,8 30 мм,
согласно ряду Ra 40 (4.8) выбираем lВ1 30 мм;
– для выходного вала II (IV)
lВ2 1,8 dВ2 1,8 25 45 мм,
согласно ряду Ra 40 выбираем lВ2 45 мм.
Примечание. Компоновочный чертеж корпуса в плане и главный вид редуктора выполняются на основании и по аналогии с §§4.4 и 4.5 из т. 3.
54

3. ОСОБЕННОСТИ РАСЧЕТА КОНИЧЕСКОЙ ЗУБЧАТОЙ
ПЕРЕДАЧИ
3.1. Общие сведения
Оси валов в конических зубчатых передачах пересекаются под углом(рис. 3.1), который обычно 90 . Зубья у конических колес выполняют прямыми и круговыми. Прямозубые конические колеса применяют при окружных скоростях до 3…8 м/с. Конические передачи имеют размеры большие, чем цилиндрические, они труднее в изготовлении и сложнее в монтаже и наладке. Шестерня в конической передаче располагается на валу консольно. Деформация консоли вала приводит к перекосу шестерни и неравномерности распределения нагрузки по длине зуба. Это приводит к снижению прочности зуба и вызывает шум.
На валах I–I и II–II расположены начальные конусы АОВ и ВОС конических зубчатых колес, которые касаются друг друга по образующей ОВ. Если вращать конус АОВ, то конус ВОС будет тоже вращаться. Каждое
коническое колесо представляет |
собой усеченный конус AA'B'B |
или |
||||
BB'C'C . Начальные конусы образуют с осями I–I и II–II углы δ |
и δ |
2 |
. Ме- |
|||
|
|
|
1 |
|
|
|
жосевой угол равен сумме δ |
δ |
2 |
90 . Основания начальных кону- |
|||
1 |
|
|
|
|
|
|
сов представляют собой диски, окружность которых называется начальной или делительной окружностью, а ее диаметр – делительным диаметром.
Делительные диаметры шестерни и колеса обозначают соответственно d1 и d2 . Образующая начальных конусов ОА, ОВ или ОС называется ко-
нусным расстоянием и обозначается буквой R.
Из треугольника КОВ находим КВ 0,5d1 , КО 0,5d2 . Используя
теорему Пифагора, определим внешнее конусное расстояние как гипотенузу треугольника КОВ:
R 0,5 d |
2 |
d |
2 |
0,5d |
1 |
sinδ |
1 |
. |
(3.1) |
|
1 |
|
2 |
|
|
|
|
Начальный конус делит зубья (рис. 3.1, а) на две части, как и в цилиндрических колесах: выше образующей конуса СО – головка зуба высотой ha , а ниже образующей СО – ножка зуба высотой hf . Высота h ha hf каж-
дого зуба больше у основания начального конуса и уменьшается к его вершине О. Внешними начальными окружностями конических колес на-
зываются окружности оснований начальных конусов. Средними начальными окружностями называются окружности оснований CтП и АтП ,
которые делят пополам усеченные конусы AA'B'B и BB'C'C . Точка П назы-
вается полюсом зацепления.
55
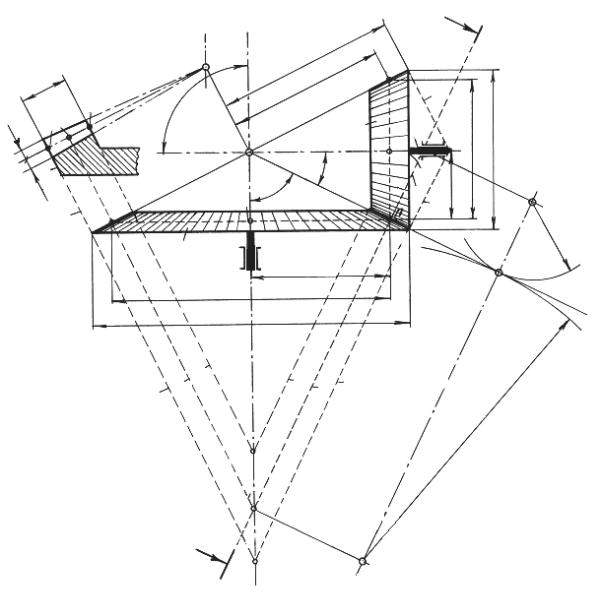
Размеры и форму конических колес определяют следующие элемен-
ты:
а) углы начальных конусов δ1 – шестерни и δ2 – колеса;
б) конусное расстояние R, представляющее собой длину образующей начального конуса;
а) элемент |
|
|
|
|
||
зубчатого венца |
|
II |
|
|||
|
|
|
|
О |
R |
|
|
|
|
|
|
|
|
b |
C ' |
|
|
Rm |
|
|
ha |
CCm |
|
Σ = 90 |
0 |
|
|
|
|
|
|
|||
|
|
|
O |
|
||
|
|
|
|
|
|
|
|
Т |
|
I |
|
δ1 |
|
|
|
|
|
δ2 |
|
|
hf |
C" |
Cm |
C ' |
|
O"2 |
|
|
1 |
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rm2 |
|
|
|
|
|
|
dm2 |
|
|
|
|
|
|
d2 |
|
|
|
|
|
3 |
3 |
2 |
|
|
|
1 |
2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
A ' |
Am |
A |
4 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
m |
|
|
|
z1 |
|
|
O'1 |
|
d |
|
|
|
|
" |
O1 |
|
|
|
|||
|
|
O 1 |
|
|
I |
1 |
сечение |
N - N |
|
|
|
|
|
d |
|||
|
|
|
K |
m1 |
|
|
|
|
B |
' |
|
5 |
|
|
' |
|
|
|
|
r |
|
|
O 1 |
|
||
|
|
|
|
4 |
|
|
|
|
|
|
B |
|
|
1 |
|
|
rэ1 |
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
П" |
1 |
|
|
|
|
|
|
|
|
2 |
1
rэ2
|
O '2 |
N |
O '2 |
|
O2 |
II Рис. 3.1
в) максимальный или внешний модуль m, который измеряется на внешнем торце T зуба CC" (см. рис. 3.1, а). Внешний модуль m является стандартным.
Передаточное отношение определяется аналогично цилиндрической передаче
56

u |
|
n1 |
|
d2 |
|
z2 |
tgδ |
|
. |
(3.2) |
|
|
d |
z |
|
||||||||
12 |
|
n |
2 |
|
|
|
2 |
|
|
||
|
|
|
1 |
1 |
|
|
|
|
|||
Геометрические размеры прямозубой конической передачи определяются по формулам:
– внешние диаметры начальных окружностей (делительные диаметры)
d1 mz1; |
d2 mz2; |
d2 u12d1; |
(3.3) |
– ширина зубчатого венца |
|
|
|
|
b ψ mm , |
|
(3.4) |
где mm – модуль в среднем сечении зуба N N (см. рис. 3.1, а); |
|
||
– внешние диаметры вершин зубьев |
|
|
|
da1 d1 2mcosδ1; |
da2 d2 2mcosδ2; |
(3.5) |
|
– углы конусов шестерни и колеса (их тангенсы)
tgδ1 z1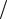 z2 i12; tgδ2 z2
z2 i12; tgδ2 z2 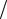 z1 u12 . (3.6)
z1 u12 . (3.6)
Средний модуль определяет размеры зуба в сечении N N и лежит в основе силовых расчетов.
Поскольку ha m [1, с. 161], то из рис. 3.1, а можно найти
mm /m Rm /R.
Из треугольника ВПЕ (рис. 3.2) определим BE 0,5b sinδ1. Находим также 0,5d1 0,5dm1 BE .
После подстановки значений d1, dm1, ВЕ и b получим
mz1 mmz1 mmψsinδ1.
Из рис. 3.1 определяем
sin δ1 |
|
0,5d1 |
|
|
d1 |
|
|
1 |
|
(3.7) |
||
R |
|
|
|
|
|
|
||||||
d12 d22 |
1 u122 |
|||||||||||
|
|
|
|
|
|
|
|
|||||
Окончательно формула для определения m имеет вид
|
|
|
ψ |
|
|
|
m m |
1 |
|
|
. |
(3.8) |
|
|
|
|
||||
|
m |
z |
1 u2 |
|
|
|
|
|
1 |
12 |
|
|
|
Эта формула применяется при эскизном проектировании.
57
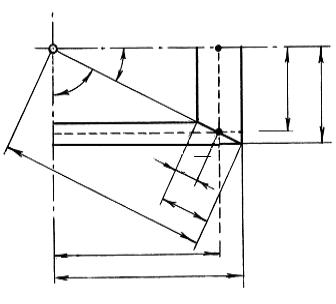
Конические колеса при геометрическом и прочностном расчетах заменяют цилиндрическими, которые соответствуют среднему сечениюN N (см. рис. 3.1, б) конических колес.
Эти цилиндрические колеса с начальными окружностями 1-1 и 2-2 называются эквивалентными. Уясним понятие эквивалентных колес и их геометрических параметров, рис. 3.1, в. Сечение N N перпендикулярно к образующей ОВ начальных конусов и проходит через середину зуба BB', которая обозначается буквой П и называется полюсом зацепления. Конусы 1, 2, 3, 4, 5 называются дополнительными конусами, а их образующие перпендикулярны к образующим начальных конусов.
O |
O1 К |
δ1
δ2
|
|
|
/2 |
/2 |
|
|
|
|
1 |
||
B |
' |
П |
m |
1 |
|
d |
d |
||||
|
Е
b
2 В
R
b
dm2/2 d2/2
Рис. 3.2
Например, треугольник OBO2 имеет прямой угол при вершине В, а треугольник OBO1 имеет прямой угол тоже при вершине В. Образующая дополнительных конусов O1O2 перпендикулярна к образующей ОВ начальных конусов.
Профилем зуба называют его контур при нормальном сечении зуба.
Нормальным сечением зуба называется сечение зуба плоскостью, перпендикулярной к продольной оси зуба B'B (см. рис. 2.1, 2.3, 3.1). Профиль зуба (см. рис. 2.2) состоит из двух боковых линий, очерченных эвольвентами, и вершины, очерченной дугой окружности вершин. Конические колеса отличаются от цилиндрических тем, что высота и толщина зубьев конических колес постепенно уменьшаются (см. рис. 3.1, а) от торца T , т.е. дополнительного конуса 1, к вершине делительных конусов О. Cответственно изменяются шаг, модуль и делительные диаметры. Для удобства измерения размеров конических колес стандартный модуль назначают на внешнем торце T , образованном дополнительным конусом 1 или 4.
Профилирование зубьев конических колес выполняют на поверхностях дополнительных конусов 1, 2, 3, 4 и 5. Если коническое колесо положить торцом T внешнего дополнительного конуса 1 (см. рис. 3.1 и 3.3) на бумагу и затем без скольжения катить его по бумаге, лежащей на плоском столе, то колесо покатится по кругу вокруг центра O2, который является вершиной дополнительного конуса 1. Аналогично, если шестерню поло-
58
жить на дополнительный конус 4, то она тоже покатится вокруг центра
O1.
Таким образом, поверхности дополнительных конусов развертываются на плоскость. При этом радиусы разверток, соответствующие точке В, равны образующим дополнительных конусов O1B и O2Bи являются радиусами наружных делительных окружностей r 1 и r 2 или делитель-
ными диаметрами d 1и d 2 наружных эквивалентных цилиндрических ко-
лес. Торец T конуса 1 оставляет на бумаге контур зубчатого венца 7 (см. рис. 3.3) вместе с профилями зубьев.
Если коническое колесо мысленно положить дополнительным конусом 2 на плоскость N N и затем без скольжения катить его вокруг цен-
тра O2' , который является вершиной среднего конуса 2, то торец Tср оста-
вит на плоскости N N контур зубчатого венца в среднем сечении. Образующая среднего конуса 2 опишет делительную окружность 8 (см. окружность 2-2 на рис. 3.1), диаметр которой равен dэ2 , а радиус - rэ2. Аналогично развертывается среднее сечение N N конической шестерни по дополнительному конусу 5, при этом развернутые цилиндрические колеса по конусам 2 и 5 называются эквивалентными цилиндрическими колесами в среднем сечении. Модуль этих колес равен mm, числа зубьев шестерни и колеса соответственно zэ1 и zэ2, делительные диаметры dэ1 и dэ2 , ширина зубчатого венца (длина зуба) b ψmm .
Итак, окружность 1-1 (см. рис. 3.1, в) есть делительная окружность эквивалентной цилиндрической шестерни диаметром dэ1. Окружность 2-2 – это делительная окружность эквивалентного цилиндрического колеса диаметром dэ2 .
Картина зацепления конических колес в среднем сечении соответствует картине зацепления цилиндрических колес диаметрами dэ1 и dэ2 , что является важным следствием, на котором основаны дальнейшие расчеты.
Для эквивалентных цилиндрических колес модулем служит средний нормальный модуль конического колеса mm, поэтому начальные диамет-
ры определяются по формулам |
|
|
|
|
dэ1 mm zэ1, |
dэ2 mm zэ2. |
(3.9) |
||
Из треугольника O'ПО" и треугольника O' ПО" найдем |
|
|||
1 |
1 |
2 |
2 |
|
rэ1 rm1 cosδ1 ; |
rэ2 rm2 cosδ2 |
rm2 sinδ1 . |
(3.10) |
|
Если эти уравнения умножить на 2, то получим |
|
|||
dэ1 dm1 |
cosδ1 ; |
dэ2 dm2 |
cosδ2 . |
(3.11) |
59
Учитывая, что делительные диаметры dm1 mmz1 и dm2 |
mmz2 , фор- |
||
мулы (3.9) можно записать в виде |
|
|
|
zэ1 z1 cosδ1 |
; zэ2 z2 cosδ2 z2 sinδ1 . |
|
(3.12) |
Конусное расстояние R, |
диаметры начальных окружностей |
d1 и d2 , |
|
угол между осями колес и конусные углы δ1 и δ2 связаны между собой. Приведем аналитические зависимости, которые понадобятся в дальнейших геометрических и силовых расчетах. Эти зависимости выведены для угла между осями колес δ1 δ2 90 .
Из рис. 3.2 и 3.1 находим величину конусного расстояния в функции делительных диаметров и углов:
– делительные радиусы, диаметры и конусное расстояние находятся в зависимости
r1 d1 |
2 R sinδ1 ; |
r2 d2 |
2 R sinδ2; |
(3.13) |
– делительные диаметры связаны между собой передаточным отношением
d2 u12 d1; |
(3.14) |
– конусное расстояние, как функция d1, d2 и u12 :
|
d |
2 |
d |
|
2 |
|
1 |
|
|
|
|
d |
|
|
|
|
|||
|
2 |
|
|
d2 |
d2u2 |
|
1 u2 . |
|
|||||||||||
R |
|
1 |
|
|
|
|
|
|
|
|
1 |
(3.15) |
|||||||
2 |
2 |
2 |
2 |
||||||||||||||||
|
|
|
|
|
|
1 |
1 12 |
|
12 |
|
|
||||||||
Передаточное отношение – функция конусных углов |
|
|
|
|
|||||||||||||||
u |
|
d2 |
|
z2 |
|
sinδ2 |
|
sinδ2 |
tgδ |
|
ctgδ , |
(3.16) |
||||||||
d |
z |
|
|
|
||||||||||||||||
12 |
|
|
|
|
sinδ |
|
|
cosδ |
2 |
|
|
|
|
2 |
1 |
|
||||
где |
1 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
r1 |
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|||
sinδ |
|
cosδ |
|
; |
|
sinδ |
|
|
cosδ . |
(3.17) |
||||||||||
|
1 |
|
R |
|
|
2 |
|
|
|
|
|
2 |
|
R |
1 |
|
||||
Зависимость синусов конусных углов в функции начальных диаметров и передаточного отношения
sinδ |
|
r1 |
|
d1 |
|
|
2d1 |
|
|
|
1 |
|
|
cosδ |
|
, |
(3.18) |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
R 2R 2d 1 u |
2 |
|
|
1 u |
2 |
|
|
2 |
|
|
|||||||
|
|
|
|
|
1 |
12 |
|
|
12 |
|
|
|
|
|
|||||
Передаточное отношение эквивалентных цилиндрических колес назы-
вается эквивалентным передаточным отношением и может быть опреде-
лено по следующей цепочке. Из треугольников O1"O1'П (см. рис. 3.1) и
O2"O2' П имеем зависимости (3.10) … (3.12). Эквивалентное передаточное отношение находим по цепочке с учетом формулы (3.12) и формулы (3.16)
60
