2336

3. Затраченная мощность на валу электродвигателя расходуется не только на преодоление полезной нагрузки, но и на потери мощности в передачах привода, муфты, ленточном транспортере и подшипниках. Она определяется по формуле

Nз Ne / 1,54/0,82 1,88 кВт.

4. Для выбора электродвигателя кроме мощности нужно еще знать его частоту вращения, которая может быть определена с помощью уравнения кинематического баланса. Это уравнение связывает между собой скорости рабочего органа и электродвигателя. В уравнении кинематического баланса (УКБ) вместо передаточного отношения применяется величина, обратная ему, которая называется передаточным числом и обозначается буквой i 1/u. Если частоту вращения двигателя (I-й вал) помножить на i12, где индексы 1 и 2 обозначают: передаточное число между I-м и II-м валами, то получим

n1 i12 n2 , (2.31)

где n2 – частота вращения второго вала. Если частоту вращения II-го вала помножить на i23, то получим

n2 i23 n1 i12 i23 n3, (2.32)

41

где n3 – частота вращения III-го вала и т.д. В нашем случае третий вал является последним. На нем смонтирован барабан ленточного транспортера.

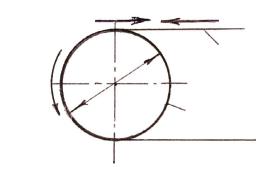
Барабан 5 и лента 6 с кинематической точки зрения представляют собой механизм преобразования движения. За 1 оборот барабана лента переместится на расстояние (рис. 2.5) Dб , а за n3 оборотов лента за 1 минуту переместится на расстояние nз Dб v. Если это значение подставить в уравнение (2.31), то получим УКБ для ленточного транспортера

цепной и зубчатой передач согласно табл. 2.3: u12 4, u23 3. Тогда пе-

редаточные числа будут равны i12 1/u12 1/4 0,25, i23 1/u23 =1/3 0,333. Решая уравнение кинематического баланса относительно n1,

получим после подстановки

n1 v/i12 i23 Dб 66/0,25 0,333 0,2 1261 об/мин.

5. По табл. 2.1 из т. 3 выбираем электродвигатель 4А90L4 мощностью Nэ 2,2 кВт и частотой вращения 1425 об/мин. Частота вращения электродвигателя больше расчетной частоты n1. Чтобы эти частоты совпадали, нужно изменить передаточное отношение редуктора i12.

6. Корректируем передаточное отношение зубчатой передачи редуктора, решая УКБ относительно i12 z1 / z2 ,

Дробь 66/298 рассматриваем как отношение чисел зубьев z1 / z2 . Так как числа очень большие, подбираем примерно ближайшее общее кратное для шестерни с условием z1 17. Задаемся z1 18. Чтобы величина дроби не изменилась, числитель и знаменатель нужно разделить на одно и то же число. Этим числом будет 66/18=3,667. Если теперь числитель и знамена-

42

i12 18/81 0,222, передаточное отношение u12 81/18 4,5.

7.Уточняем скорость транспортера, используя УКБ,

vnэ i12 i23 Dб 1425 0,222 0,333 0,2 66,19 м/мин

или v 66,19 м/мин=1,103 м/с. Погрешности расчета скорости

где vp – расчетное значение скорости; v – заданное значение скорости.

Результаты расчетов – удовлетворительные.

8. Определяем по известным формулам угловые скорости и частоты вращения валов.

8.1. 1-й вал:

– частота вращения n1 nэ 1425 об/мин;

–угловую скорость определим по формуле

n/30 n/9,55;

подставляя числовые значения для первого вала, получим

1 n1 /9,55 1425/9,55 149 с-1.

8.2. 2-й вал:

– частоту вращения определим по формуле (2.31)

43

n2 n1 i12 1425 0,222 316 об/мин;

– угловую скорость найдем по формуле (2.33)

2 n2 /9,55 316/9,55 33 с-1.

8.3.3-й вал:

–частоту вращения вычислим по формуле (2.32)

n3 n1 i12 i23 1425 0,222 0,333 105 об/мин;

– угловую скорость определим по п. 8.1

3 n3 /9,55 105/9,55 11 с-1.

9. Для расчетов на прочность и жесткость нужно знать величину крутящих моментов на валах. Индекс при символе крутящего момента или мощности обозначает номер вала.

9.1. 1-й вал. Расчет крутящего момента на 1-м валу проводится по формуле

где N1 – мощность на 1-м валу (мощность электродвигателя), кВт; n1 –

частота вращения первого вала; м 0,98 – КПД муфты; 2п – КПД пары подшипников.

Подставляя числовые значения в формулу (2.33), получим

М1 9,55 2,2 0,98 0,99 1425 0,0143 Кнּм=14,3 Нּм.

9.2.2-й вал. Крутящий момент определяется по формуле

где u12 4,5 – передаточное отношение между 1-м и 2-м валами;

12 зп 2п 0,98 0,99 0,97.

После подстановки получим

М2 14,3 4,5 0,97 62,42 Нּм.

9.3.3-й вал. По аналогии с формулой (2.34) найдем величину крутящего момента на 3-м валу

44

где u23 3 – передаточное отношение между 2-м и 3-м валами;

23 уп 2п 0,93 0,99 0,92.

Подставляя числовые значения, получим

М3 62,42 3 0,92 172,28 172 Нּм.

10.Проверяем тяговую силу ленточного транспортера, которую найдем из условия равенства работ. Движущей силой выступает (см. рис. 2.5) крутящий момент на 3-м валу, который расходуется на преодоление тяговой силы Ft , т.е. силы сопротивления, и потерь в ременной передаче лен-

точного транспортера, которые оцениваются коэффициентом полезного действия рп . Условие равенства работ выражается формулой, которая со-

ставлена для одного оборота 3-го вала

2 Mз рп Ft Dб .

Сокращая число и решая уравнение относительно Ft , получим

Ft 2 172 0,95/0,2 1634 Н=1,634 кН.

В результате выбора двигателя большей мощности тяговая сила увеличилась на

F (Ftр Ft) 100/Ft (1,634 1,4) 100/1,4 16,7 %,

где Ftр – расчетное значение тяговой силы; Ft – заданное значение тяго-

вой силы.

11. Выбираем материал шестерни сталь 45 улучшенная, НВ=300, материал колеса – сталь 40Х улучшенная, НВ=240. Термообработка обычно производится до нарезания зубьев колес с той целью, чтобы после нарезания зубьев на станке полученная высокая точность не искажалась при термообработке. Сталь с твердостью НВ<350 после термообработки хорошо обрабатывается инструментом из быстрорежущих сталей. 8-я степень точности обеспечивается уверенно на зубофрезерных и зубодолбежных станках. 7-я степень точности требует тонкого фрезерования и долбления или дополнительной отделочной операции – шевингования. Шевингованием достигают 7-ю и 6-ю степени точности зубчатых колес.

После фрезерования и долбления зубья колес хорошо прирабатываются (прикатываются) друг по другу. Для лучшей приработки зубьев и рав-

45

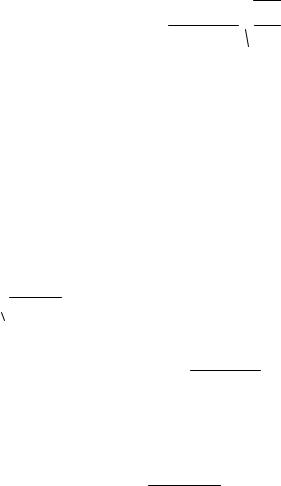
номерного изнашивания твердость рабочих (боковых) поверхностей зубьев шестерни делают больше твердости зубьев колеса. Для прямозубых передач твердость зубьев шестерни выбирают на 20…30 единиц НВ больше, чем колеса. Например, шестерня – 280 НВ, а колесо 250 НВ. Дело в том, что каждый зуб шестерни входит в зацепление с колесом в u12 раз чаще, где u12 – передаточное отношение. За 1 оборот колеса шестерня повернется u12 z1 раз. Поэтому шестерня больше изнашивается и вероятность ее усталостного разрушения выше.

Для косозубых и шевронных колес разность в твердости шестерни и колеса делают еще больше: НВш-НВк=60…80, где НВш – твердость по Бринелю зубьев шестерни, НВк – твердость зубьев колеса. Это позволяет повысить нагрузочную способность передачи на 25…30 %.

Улучшенные стали применяются марок 40, 45, 40Х.

Для выбранного материала определим допускаемый коэффициент контактных напряжений по формулам (2.22) и (2.23)

Сн НВ 1003No , 100 N

где НВ – твердость зубьев по Бринелю; No 20 106 – базовое число циклов; N – действительное число циклов перемены напряжений, которое найдем после подстановки частоты вращения шестерни n1 1425 об/мин и времени работы передачи h 10000ч в формулу (2.25)

N1 60 1425 104 8,55 108,

для колеса n2 316 об/мин, а действительное число циклов

N2 60 316 104 1,9 108.

Так как 3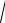No / N 1 для шестерни и колеса, формула (2.22) принима-

ет вид

Сн НВ 100. 100

После подстановки твердости получим

– для шестерни

Сн 300 100 2 Н/мм2, 100

– для колеса

46

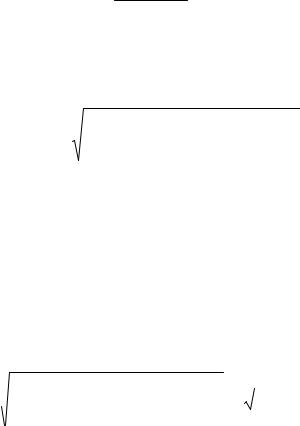
Сн 240 100 1,4 Н/мм2. 100

Для расчетов выбираем меньшее значение, т.е. Сн 1,4 Н/мм2.

12. Торцевой модуль косозубых и шевронных колес определяется по формуле (2.21)

отношение между 1-м и 2-м валами; Сн 1,4 Н/мм2 – коэффициент кон-

терни. После подстановки числовых значений в формулу (2.21) получим

13.Межцентровое расстояние найдем по формуле (2.10)

а0,5mt (z1 z2) 0,5 1,996(18 81) 98,8 мм.

Поскольку модуль нужно округлять в большую сторону, т.к. стоит знак , межцентровое расстояние округляем до ближайшего большего согласно стандартному ряду Ra 40 (см. т. 3, табл. 3.2) a 100 мм.

14.Уточняем торцевой модуль, преобразуя формулу (2.10) mt 2a/(z1 z2) 2 100/(18 81) 2,02 мм.

15.В качестве нормального модуля выбираем ближайшее меньшее согласно стандартному ряду:

1-й ряд: 1; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10.

2-й ряд: 1,25; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9.

Ближайший меньший стандартный модуль mn 2 мм. Тогда угол на-

клона зуба найдем из формулы (2.5)

arccos(mn /mt ) arccos(2/1,02) 8,070 804'.

Рекомендуемый угол наклона зуба 8 ...180 . Следовательно, результат удовлетворительный.

47

16. Определяем геометрические параметры зубчатых колес:

16.1.Делительный диаметр шестерни, формула (2.7) d1 mt z1 2,02 18 36,36 мм.

16.2.Делительный диаметр колеса

d2 mt z2 2,02 81 163,64 мм.

Проверка. Межцентровое расстояние, формула (2.10)

a12 (d1 d2)/2 (36,36 163,64)/2 100 мм.

Результаты расчета удовлетворительные.

16.3. Диаметр вершин зубьев шестерни, формула (2.8)

da1 mt z1 2mп 2,02 18 2 2 40,36 мм.

16.4. Диаметр вершин зубьев колеса

da2 mt z2 2mп 163,64 2 2 167,64 мм.

16.5. Ширину зубчатых колес по формуле

где m 10...20 – коэффициент ширины зуба; mn – нормальный модуль. Ширину колеса после вычисления округляют в ближайшую сторону до стандартного ряда Ra 40 (см. т. 3, табл. 3.2).

После подстановки числовых значений получим

b10 2 20 мм.

17.Теперь переключаемся на методику расчета и компоновки цилиндрических зубчатых колес, валов и подшипников (т. 3, § 4.3).

Исходные данные: числа зубьев шестерни и колеса z1 18, z2 81;

модули: нормальный mn 2 мм, торцевой mt 2,02 мм; угол наклона зубьев 8,070 ; диаметры: шестерни d1 36,36 мм, da1 40,36 мм, колеса d2 163,64 мм, da2 167,64 мм; межцентровое расстояние a 100 мм; ширина b 20 мм; моменты крутящие: на 1-м валу M1 14,3Н·м, на 2-м

валу M2 62,42Н·м.

Нужно провести расчет и скомпоновать чертеж.

17.1. Выписываем в исходные данные геометрические размеры зубчатых колес из пп.16.1…16.5.

48

17.2.Вычисляем размер с (т. 3, рис. 4.2) от торца зубчатых колес до середины подшипников, т.е. их оси симметрии слева и справа от колес по эмпирической формуле

с10mn 10 2 20 мм.

17.3.Определяем размер ао (см. т. 3, рис. 4.2) от оси симметрии зубчатых колес до оси симметрии подшипников

ао с 0,5b 20 0,5 20 30 мм.

17.4. Теперь на миллиметровке в масштабе 1:1 тонкими линиями вычерчиваем контуры зубчатых колес без ступиц (т. 3, рис. 4.3) и проводим оси валов. При этом должно выдерживаться межцентровое расстояние а12 (см. т. 3, рис. 4.3 это а34). Затем проводим перпендикулярно к осям валов оси симметрии подшипников на расстоянии с от торцев зубчатых колес по обе стороны.

Далее переходим к построению ступенчатых валов.

17.5. На рис. 4.3, т. 3, вал III соответствует нашему валу I, а вал IV – нашему валу II.

Наименьшими диаметрами валов I и II, III и IV являются диаметры входной шейки dВ1 (dВ3 ) и выходной шейки dВ2 (dВ4). В дальнейших расчетах и описании будем наши параметры писать без скобок, а параметры соответствующие т. 3, рис. 4.3, – в скобках. Наименьшие диаметры рассчитываются по формуле (4.1), т. 3

где dВi – диаметры входной и выходной шеек, мм; Mi – крутящий момент на i валу, Н·мм; k 50...63 Н/мм2, для быстроходного вала k 50 Н/мм2 , для тихоходного вала k 63 Н/мм2 – допускаемое напряжение.

Для первого (третьего) вала после подстановки числовых значений, если k 50 Н/мм2, получим

Диаметры валов рекомендуется округлять до стандартного ряда Ra 20: 10; 11; 12; 14; 16; 18; 20; 22; 25; 28; 32; 36; 40; 45; 50; 56; 63; 71; 80; 90; 100.

Для второго (четвертого) вала, подставляя числовые значения, найдем, если k 63 Н/мм2,

49

приведен после проверки пригодности выбранных подшипников.

За ними следуют шейки валов под подшипники диаметрами dП1 (dП3) и dП2 (dП4), которые можно определить с помощью эмпирической фор-

мулы (4.2), т. 3,

dПi dУi 0...4 dВi 2t3 0...4,

где t3 – высота заплечика (т. 3, табл. 4.7); цифра 2 – для меньших диаметров, цифра 4 – для больших диаметров.

На эти шейки одеваются подшипники своим отверстием диаметра dП (т. 3, рис. 4.4). Внутренние диаметры подшипников качения, начиная с 20 мм, оканчиваются на 0 и на 5, так построен стандартный ряд: 20, 25, 30, 35, 40, 45, 50,…100 мм. Если две последние цифры номера подшипника умножить на 5, то получим внутренний диаметр dП . Например, подшипник №205, его внутренний диаметр dП 5 5 25 мм; подшипник №311, его внутренний диаметр dП 11 5 55 мм и т.д. Внутренний диаметр является главным размером подшипников, поэтому они подбираются по диаметру отверстия dП . Индекс П в справочных таблицах отсутствует, поэтому диаметр отверстия в них обозначается d . В пособии диаметр шейки вала и отверстие в подшипнике будем обозначать dП .

Определяем внутренний диаметр подшипника на I (III) валу

dП1 dВ1 2t3 0...4 16 2 3,5 2 25 мм.

на II (IV) валу

dП2 dВ2 2t3 0...4 25 2 4,5 1 35 мм.

17.7. Согласно рекомендациям (гл. 4) в цилиндрических прямозубых и косозубых редукторах применяют шариковые радиальные подшипники, которые помимо радиальной нагрузки могут воспринимать еще и осевую до 25 % от радиальной, т.е. работать как радиально-упорный шарикоподшипник.

По табл. 4.1, т. 3, выбираем радиальные однорядные шариковые подшипники легкой серии №205 для вала I и №207 для вала II. Динамическая грузоподъемность их С1 14 кН и С2 25,5 кН, моменты крутящие

50