
2330
.pdf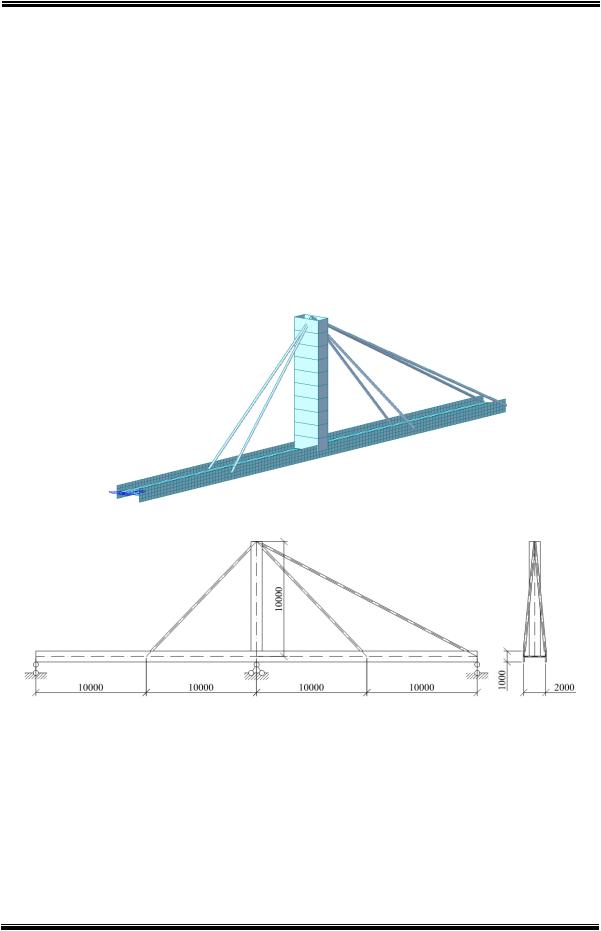
СТРОИТЕЛЬСТВО. СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ И ИЗДЕЛИЯ
Нетрудно видеть, что в начальный момент при t 0 из выражения (4) найдем z(0) B0 jψ j ,
т.е. перемещения узловых линий соответствуют начальному состоянию неповрежденной конструкции. Наибольшие отклонения можно приближенно
определить, |
приняв |
t / 1 , |
тогда |
z (2Bs1 B01)ψ1 Если пренебречь начальной скоростью ( Aj 0), колебания будут происходить
около статического положения поврежденной конструкции, которое приближенно можно определить,
полагая t /(2 1 ), где 1 – первая круговая
частота свободных колебаний моста без одной ванты. Следует заметить, что выше использованы две расчетные модели моста. Первая модель неповрежденной конструкции нужна для определения статического положения моста в момент обрыва
ванты (z0k ), вторая модель – статического поло-
жения zsk , собственных форм ψj и исследования
динамики моста без одной ванты.
Применение метода конечно-элементного моделирования.
Рассмотрим конечно-элементную модель простейшей пространственной вантовой системы, изображенной на рисунках 1 и 2. Пространственная модель вантового моста состоит из пилона, балки и вант. Пилон смоделирован при помощи балочного конечного элемента. Призматический 3D балочный элемент определяют два узла. Каждый узел имеет три поступательные и три вращательные степени свободы. Элемент учитывает жесткость пилона на растяжение-сжатие, на изгиб, на сдвиг и на кручение. Пилон состоит из 10 таких элементов.
Рис. 1. Общий вид вантовой системы.
Рис. 2. Геометрические размеры вантовой системы.
Балка задана пластинчатыми конечными эле- |
E=2.06∙108 кПа, коэффициентом Пуассона k=0.2 и |
ментами. Пластинчатый конечный элемент опре- |
объемным весом p=76.98 кН/м3. Балка жесткости |
деляют 4 узла, расположенных в одной плоскости. |
имеет двутавровое сечение высотой 1 м, шириной |
Балка состоит из 1440 таких элементов, средний |
2 м и толщиной 0.1 м. Пилон задан коробчатым |
размер составляет 0.333x0.3 м. Ванта смоделиро- |
сечением: А=0.6 м2, Jx=0.2667 м4, Jx=0.1175 м4. |
вана элементом работающим только на растяже- |
Ванты заданы круглым сечением площадью А=0.06 |
ние. Работающий только на растяжение линейный |
м2 без предварительного натяжения. Балка закре- |
элемент пространственной конструкции определя- |
плена согласно рисунку 1, пилон в основании за- |
ется двумя узлами. Этот элемент испытывает |
креплен жестко. |
только осевую деформацию. Таких элементов в |
Производим три независимых расчета на дей- |
системе столько же сколько и вант. |
ствие собственного веса: статический с целыми |
Материал для всех элементов вантовой систе- |
вантами, статический с одной оборванной в сече- |
мы определен как сталь с модулем упругости |
нии x=10 м, и динамический с обрывам вант в том |
Вестник СибАДИ, выпуск 4 (22), 2011 |
21 |

СТРОИТЕЛЬСТВО. СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ И ИЗДЕЛИЯ
же сечении. При каждом расчете определяем со- |
вая вынужденных колебаний балки согласно рисун- |
гласно рисунку 3, в узлах 2 и 5 перемещения, в |
ку 4. К 50 секундам нагрузка возрастает до 100%. В |
узлах 1,3,4 и 6 нормальные напряжения. |
диапазоне от 50 до 60 секунд при полных нагрузках |
|
вантовая система работает как «статическая схема |
|
с целой вантой». В 60 секунд кривая изменения |
|
сил, компенсирующих работу ванты, мгновенно |
|
падает до нуля, и возникает эффект «обрыва ван- |
|
ты». Обрыв ванты вызывает колебания вантовой |
|
системы. |
|
Для анализа трех состояний вантовой системы по- |
|
строим график перемещений для узловой линии 5. |
Рис. 3. Сечение балки. |
|
Первые два расчета довольно просты, поэтому |
|
описаны не будут. Следует отметить, что третий |
|
расчет выполнен в динамической постановке. |
|
Плотность материала и собственный вес всех эле- |
|
ментов вантовой системы учтены. |
|
Удаляем одну ванту, прикрепленную к узловой |
|
линии 5 в сечении х=10м, а в качестве компенсации |
|
на балку жесткости и пилон прикладываем сосре- |
|
доточенные силы, равные продольной силе в от- |
|
брошенной ванте. Рассматривается простое квази- |
|
статическое (медленное) нагружение, когда все |
|
нагрузки, включая реакцию отброшенной ванты, |
Рис. 4. Изменения сил во времени. |
меняются во времени пропорционально одному |
|
параметру. Собственный вес и силы, компенси- |
|
рующие работу ванты, плавно нарастают не вызы- |
|
Рис. 5. Вертикальные перещения (мм) для трех состояний конструкций.
Заключение |
Библиографический список |
На основании изложенного можно заключить, |
|
что применение модели складки с методом разло- |
1. Александров А.В. Строительная механика. |
жения по собственным формам позволяет допол- |
Тонкостенные пространственные системы/ А.В. |
нительно к проведенным расчетам с использова- |
Александров, Б.Я. Лащеников, Н.Н. Шапошников. – |
нием больших программных МКЭ-комплексов вы- |
М.: Стройиздат, 1983. – 488 с. |
полнить качественный анализ динамики сложной |
2. Гулд С. Вариационные методы в задачах о |
конструкции |
собственных значениях. – М.: Мир, 1970.–328 с. |
22 |
Вестник СибАДИ, выпуск 4 (22), 2011 |

СТРОИТЕЛЬСТВО. СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ И ИЗДЕЛИЯ
3. Вибрации в технике: Справочник._М: Маши-
ностроение, 1978.–Т1.–352 с.
DYNAMICS CABLE-STAYED BRIDGE AFTER
BREAKAGE STAY CABLE
G.M. Kadisov, V.V. Chernyshov
The fold model of the mixed method of dynamic analysis of cable-stayed bridge is offered, that is used for comparison with results received by FEM analysis.
Кадисов Григорий Михайлович - доктор технических наук, профессор, заведующий кафедрой
УДК 625.7
«Строительная механика», Сибирская государственная автомобильно-дорожная академия (СибАДИ). Основное направление научных исследований: статика, динамика и устойчивость пространственных конструкций. Общее количество публикаций 60. Е-mail: kadisov@rambler.ru
Чернышов Виталий Витальевич - аспирант Сибирская государственная автомобильнодорожная академия. Основное направление научных исследований: мосты, динамика сооружений. Общее количество публикаций 2.
Е-mail: Chervv@mail.ru
ОБ ОПРЕДЕЛЕНИИ ПРЕДЕЛА ПРОЧНОСТИ АСФАЛЬТОБЕТОНА НА РАСТЯЖЕНИЕ ПРИ ИЗГИБЕ
Г.М. Левашов, В.В. Сиротюк
Аннотация. В статье рассматривается возможность применения существующих положений сопротивления материалов к оценке предела прочности асфальтобетона на растяжение при изгибе. Приведены результаты испытаний.
Ключевые слова: предел прочности, асфальтобетон, одноосное растяжение, сжатие, изгиб.
Введение |
мативные характеристики асфальтобетона при |
В действующем нормативном документе по |
изгибе путём механических испытаний образцов- |
проектированию нежёстких дорожных одежд ОДН |
балочек размером 40х40х160 мм по ГОСТ 12801-98 |
218.046-01 [1] к основным расчётным параметрам |
[3]. Таким образом, на данный момент нет даже |
асфальтобетона относятся значения модуля упру- |
единого нормированного подхода к методике про- |
гости и сопротивления растяжению при изгибе. В |
ведения испытаний асфальтобетона на растяже- |
этом документе произошло практически четырёх- |
ние при изгибе. |
кратное увеличение расчётного значения предела |
В то же время в строительной отрасли дейст- |
прочности на растяжение при изгибе по сравнению |
вуют другие, более «строгие» документы [5, 6, 7], |
с ранее действующим документом. Так, в соответ- |
по которым расчёт цементобетонных (железобе- |
ствии с отменённым ВСН 46-83 [2], для плотного |
тонных) элементов на изгиб производится с помо- |
асфальтобетона на битуме БНД 90/130 предел |
щью зависимостей теории упругости по норматив- |
прочности составлял 2,4 МПа, а в изданном взамен |
ным значениям прочности на одноосное сжатие и |
ОДН 218.046-01 [1] – увеличился до 9,5 МПа. При |
растяжение. |
этом многие авторы отмечают невозможность по- |
Рассмотрим, как избежать вышеуказанных про- |
лучения в лабораторных условиях столь высоких |
тиворечий и вернуться к классическим решениям |
значений этого показателя. |
сопротивления материалов. |
Такая вольная трактовка значений расчётной |
Основная часть |
характеристики возможна только при отсутствии |
Принято, что значение предела прочности на |
достоверного теоретического решения. Авторы |
растяжение при изгибе (величина максимальных |
вышеуказанных документов базируются на «назна- |
нормальных горизонтальных напряжений) устанав- |
ченных» ими нормативных значениях расчётных |
ливается по результатам нагружения образца в |
параметров и нормативной методике определения |
виде балки сосредоточенной силой посередине |
предела прочности на растяжение при изгибе [3]. |
пролета. Анализировать расчётную схему испыта- |
Однако в ГОСТ 12801-98 [3], устанавливающем |
ний образца-балки на изгиб необходимо с позиции, |
методы испытаний материалов на основе органи- |
что асфальтобетон, как и большинство других ма- |
ческих вяжущих, нет чёткого указания о примени- |
териалов (пластмассы, цементобетон и др.) имеет |
мости этого документа для испытания образцов в |
различные модули упругости при растяжении и |
виде балок из асфальтобетона. В то же время, |
сжатии. Обозначим модуль упругости при растяже- |
пункт 7.10 действующего Пособия по строительству |
нии Е1, а при сжатии – Е2. Вследствие того, что |
асфальтобетонных покрытий и оснований автомо- |
модули упругости при сжатии и растяжении раз- |
бильных дорог и аэродромов (к СНиП 3.06.03-85) |
личны, эпюра горизонтальных напряжений имеет |
[4] рекомендует определять прочностные и дефор- |
излом по нейтральной оси. |
Вестник СибАДИ, выпуск 4 (22), 2011 |
23 |
СТРОИТЕЛЬСТВО. СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ И ИЗДЕЛИЯ
Тогда горизонтальные нормальные напряже- |
требованиям ГОСТ 12801-98 [3]. Обработка ре- |
||||||||||||||||||||||
ния в растянутой (σ1) и сжатой (σ2) зонах составят |
зультатов испытаний заключалась в определении |
||||||||||||||||||||||
по [8]: |
|
Mx |
|
|
|
|
|
|
|
|
|
|
|
Mx |
|
|
предела прочности при одноосном растяжении |
||||||
|
E1 |
|
|
|
|
|
|
|
|
|
E2 |
|
, |
(1) |
рас (МПа), относительной вертикальной дефор- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
σ1= Eприв |
|
|
|
J |
|
y1;σ2= Eприв |
|
J |
y2 |
|
мация ε и модуля деформации при растяжении |
||||||||||||
где Е1, Е2 – модуль упругости асфальтобетона при |
Eдрас (МПа). |
||||||||||||||||||||||
растяжении и при сжатии, соответственно; J – мо- |
|
||||||||||||||||||||||
мент инерции всего сечения относительно цен- |
|
||||||||||||||||||||||
тральной оси; Mx – величина действующего изги- |
|
||||||||||||||||||||||
бающего момента; Еприв – приведённый модуль |
|
||||||||||||||||||||||
упругости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Высота растянутой зоны при этом определяет- |
|
||||||||||||||||||||||
ся как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
h1 |
|
|
|
|
|
E2 |
|
|
|
|
h |
, |
|
|
|
|
|
|
(2) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
E1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
E2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
где h – общая высота сечения балки. |
|
|
|
||||||||||||||||||||
Значение приведённого модуля упругости, рас- |
|
||||||||||||||||||||||
считывалось по формуле, предложенной |
проф. |
|
|||||||||||||||||||||
Ф.С. Ясинским [8]: |
|
|
|
|
|
|
4E1E2 . |
|
|
|
(3) |
|
|||||||||||
Eприв |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||
E1 |
E2 |
|
|
|
|
|
|||||||||||||||||
Формулы, полученные выше, справедливы только в том, случае, когда изгиб происходит в пределах упругих деформаций.
Рассмотрим теперь более сложную задачу, когда возрастающая нагрузка Р доведёт систему до разрушения. Вначале балка будет работать в пределах упругих деформаций. Затем в середине пролёта при некотором значении момента М в наиболее нагруженной точке напряжения достигают предела текучести. При увеличении нагрузки пластическая зона постепенно проникает вглубь сечения. Интенсивно нарастающие деформации концентрируются в наиболее напряжённом сечении (в нашем случае под грузом), в этом месте появится так называемый пластический шарнир. Момент в этом сечении достигнет предельной величины разрушающего момента Мраз [8].
Значение разрушающего момента внутренних сил относительно нейтральной оси в этом случае определяется по формуле:
|
h2 |
|
h2 |
|
|||
Mxраз трас |
1 |
b |
тсж |
2 |
b. |
(4) |
|
2 |
2 |
||||||
|
|
|
|
|
|||
Возможность применения (1) и (4) для определения расчётным путём предела прочности асфальтобетона на растяжение при изгибе, ограничивается тем, что нет и нормированной методики определения предела прочности асфальтобетона на одноосное растяжение [9].
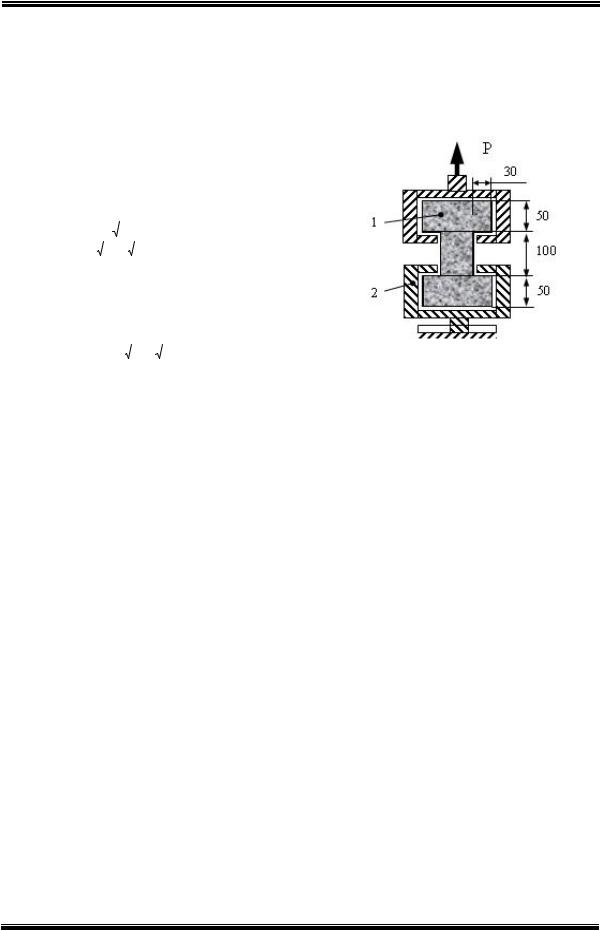
Мы использовали методику, суть которой отражена на рисунке 1. Для испытаний использовали образцы из асфальтобетона «гантелеобразной» формы, полученные путём выпиливания циркулярной пилой с алмазными дисками из образцов с размерами 200х100х40 мм, изготовленных на «стенде СибАДИ» [10]. Испытания проводили при температурах образцов: (минус 20±2) °С, (0±2) °С, (20±2) °С и (40±2) °С на универсальной испытательной машине GOTECH UG-LA10 при постоянной скорости нагружения (3,0±0,3) мм/мин. согласно
Рис. 1. Испытания по определиению предела прочности на растяжение: 1 – асфальтобетонный
образец; 2 – металлические захваты
Параллельно проводились испытания по определению предела прочности при сжатии асфальтобетона по стандартной методике [3]. При этом было испытано по восемь образцов при каждой фиксированной температуре: (минус 20±2) °С, (0±2) °С, (20±2) °С и (40±2) °С.
Подобрана корреляционная зависимость (с коэффициентом корреляции R2 = 0,98), связывающая предел прочности при растяжении и предел прочности при сжатии асфальтобетона:
Враст 0,015 Всж 2 |
0,476 Враст 0,397. |
Таким образом, предел прочности асфальтобетона при растяжении находится в диапазоне от 20% до 35% от предела прочности при сжатии в зависимости от его температуры.
В ходе экспериментальных исследований установлено наличие линейной корреляционной зависимости между модулем упругости асфальтобетона при сжатии и при растяжении. Так, при температуре 0 оС имеем Ераст = 0,40∙Есж. Тогда при расчётном значении температуры 0 оС, высота растянутой зоны (положение нейтральная оси от нижней грани элемента), определенная по формуле (2) составит h1 = 0,615∙h. А при температуре 20 оС – Ераст = 0,16∙Есж и h1 = 0,715∙h.
Получается, что при расчётной температуре, растянутая зона будет занимать примерно 2/3 от общей высоты сечения асфальтобетонного образца – балки.
Полученное соотношение между высотой поперечного сечения сжатой и растянутой зоны проверено экспериментальным методом.
Сущность этого метода состоит в определении горизонтальных деформаций по высоте сечения асфальтобетонной балки при изгибе. Для чего с
24 |
Вестник СибАДИ, выпуск 4 (22), 2011 |

СТРОИТЕЛЬСТВО. СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ И ИЗДЕЛИЯ
помощью аэрозольных красок и перманентного маркера на боковую грань балки наносилась сетка с шагом 10 мм (рисунок 2).
Рис. 2. Пример построения сетки для определения относительных деформаций (а); эпюра горизонтальных деформаций (б): 1 – эксперименталь-
ные данные, 2 – теоретические данные
Спомощью видеоаппаратуры фиксировалось положение узлов сетки до приложения нагрузки и в процессе нагружения (для примера расчёта выбрана нагрузка равная 30 % от разрушающей). На каждом цифровом фотоснимке назначалась одна и та же базовая точка (точка начала координат) и определялось положение узлов сетки в декартовых координатах. Единицей измерения при создании декартовых координат служил один пиксель изображения. В результате измерений координат узлов сетки до и после приложения нагрузки определяли изменения относительных вертикальных и горизонтальных деформаций по толщине асфальтобетонной балки.
На рисунке 2 б представлена эпюра относительных горизонтальных деформаций по толщине сечения асфальтобетонной балки в точке приложения силы. Неравномерность этой эпюры объясняется неоднородной структурой асфальтобетона (наличием фракций крупного заполнителя до 20 мм).
Для экспериментального определения положения нейтральной оси при изгибе асфальтобетонной балки было испытано восемь асфальтобетонных образцов при температуре (20±2) °С. Результаты испытаний свидетельствуют о достоверности наших расчётов: погрешность между теоретическим и экспериментальным результатами не превышала 6 %.
Результаты экспериментальных исследований подтверждают достоверность выдвинутой гипотезы
оположении нейтральной линии в асфальтобетоне при изгибе. Нейтральная ось, в нашем случае, не проходит через центр тяжести сечения, а разделяет сечение на две неравные части.
Сучётом положений, описанных выше, результаты испытаний по определению предела прочности асфальтобетона на растяжение при изгибе (МПа) предлагается обрабатывать по формуле:
|
E |
|
M |
р |
, |
(5) |
|
В |
|
1 |
|
|
х |
h1 |
|
|
|
J |
|
|
|||
|
Eприв |
|
|
|
|
||
где M p Pl – величина разрушающего изгибаю-
x 4
щего момента, Н∙мм; P - величина разрушающей
нагрузки, Н; l – расстояние между опорами (пролёт), мм; Eприв – значение приведённого модуля упругости определяется по (3), МПа; h1 – высота растянутой зоны определяется по (2), мм; Е1 – модуль упругости асфальтобетона на растяжение, МПа.
Напомним, что в соответствии с действующими нормативными документами [1, 3] принято, что асфальтобетон имеет одинаковые значения модуля упругости на растяжение и сжатие, тогда нейтральная ось проходит через центр тяжести поперечного сечения, т.е. hраст.з = 0,5∙h. В этом случае, формула (5) примет привычный вид:
|
В |
|
3Pl |
10 2 , |
(6) |
|
2bh2 |
||||||
|
|
|
|
где P – величина разрушающей нагрузки, кН; l – величина пролета балки (расстояние между опорами), см; b, h – ширина и высота поперечного сечения балки, см;
Для определения предела прочности на растяжение при изгибе асфальтобетона было испытано по восемь образцов при каждой фиксированной температуре. По результатам испытаний подобрана корреляционная зависимость, связывающая предел прочности на растяжение при изгибе асфальтобетона (σВ, МПа) с его температурой (Т, °С). На рисунке 3 представлена графическая интерпретация полученной зависимости.
Рис. 3. Зависимость предела прочности на растяжение при изгибе асфальтобетона
от температуры испытаний
Сопоставление экспериментальных данных с теоретическим решением по формулам (1) и (4) показывает, что расхождение экспериментальных данных с теоретическими не более 10 % при температуре минус 20 °С, и не более 5 % при температуре 20 °С.
Заключение
Результаты исследования показывают возможность применения теории изгиба конструкций, изготавливаемых из материалов, обладающих различными модулями упругости на растяжение и сжатие, с учётом принципа «образования пластического шарнира», при оценке прочностных характеристик асфальтобетона.
Наши исследования будут продолжены, но даже полученные результаты свидетельствуют о воз-
Вестник СибАДИ, выпуск 4 (22), 2011 |
25 |

СТРОИТЕЛЬСТВО. СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ И ИЗДЕЛИЯ
можности определения более обоснованных значений предела прочности асфальтобетона на растяжение при изгибе, что в свою очередь будет способствовать более качественному анализу экспериментальных данных, особенно при назначении расчётных нормативных значений для проектирования нежёстких дорожных одежд.
Библиографический список
1.ОДН 218.046-01 Проектирование нежестких дорожных одежд [Электрон. ресурс]. – Введен 2001-01-01 // Кодекс. Право / ЗАО «Информационная компания «Кодекс». – СПб., 2011.
2.ВСН 46-83 Инструкция по проектированию дорожных одежд нежесткого типа [Электрон. ре-
сурс]. – Введен 1984-01-01, отменен 2001-01-01 //
Кодекс. Право / ЗАО «Информационная компания
«Кодекс». – СПб., 2011.
3.ГОСТ 12801-98 Материалы на основе органических вяжущих для дорожного и аэродромного строительства [Электрон. ресурс]. – Введен 1999- 01-01 // Кодекс. Право / ЗАО «Информационная компания «Кодекс». – СПб., 2011.
4.Пособие по строительству асфальтобетонных покрытий и оснований автомобильных дорог и аэродромов (к СНиП 3.06.03-85) [Электрон. ресурс]
//Кодекс. Право / ЗАО «Информационная компания
«Кодекс». – СПб., 2011.
5.СП 52-101-2003 Бетонные и железобетонные конструкции без предварительного напряжения арматуры [Электрон. ресурс] – Введен 2004-03-01 // Кодекс. Право / ЗАО «Информационная компания
«Кодекс». – СПб., 2011.
6.Пособие по проектированию бетонных и железобетонных конструкций из тяжелого бетона без предварительного напряжения арматуры (к СП 52- 101-2003) [Электрон. ресурс] // Кодекс. Право / ЗАО «Информационная компания «Кодекс». – СПб., 2011.
7.СП 35.13330.2011 Мосты и трубы. Актуализированная редакция СНиП 2.05.03-84* [Электрон.
УДК 624.012
ресурс] – Введен 2011-05-20 // Кодекс. Право / ЗАО «Информационная компания «Кодекс». – СПб., 2011.
8.Сопротивление материалов. Под ред. А.Ф. Смирнова. Учебники для вузов. Изд. 3-е, перераб. и.доп. М.: «Высшая школа», 1975. – 480 с.
9.Автомобильные дороги и мосты. Проектирование состава асфальтобетона и методы его испытаний / Обзорная информация. –М.: Информавто-
дор, 2005. –Вып.6. -62с.
10.Сиротюк В.В., Крашенинин Е.Ю. Лабораторный метод изготовления армированных асфальтобетонных образцов /Вестник ТГАСУ. -Томск:
Изд-во ТГАСУ, 2007. -С.54-60.
ABOUT DEFINITION ULTIMATE TENSILE STRENGTH BENDING A BEAM OF ASPHALT
CONCRETE
G.M. Levashov, V.V. Sirotuk
Possibility of application the existing positions resistance materials to a definition ultimate tensile strength bending a beam of asphalt concrete is shown. Results of tests are brought.
Сиротюк Виктор Владимирович – д-р техн. наук, проф., зав. кафедрой «Проектирование дорог» Сибирской государственной автомобильнодорожной академии (СибАДИ). Применение геосинтетических материалов в дорожных конструкциях, применение золошлаковых смесей в дорожном строительстве. Общее количество пуб-
ликаций – 206 . E-mail: sirotuk_vv@sibadi.org.
Левашов Григорий Михайлович – преподаватель кафедры «Проектирование дорог» Сибирской государственной автомобильно-дорожной академии (СибАДИ). Применение геосинтетических материалов в дорожных конструкциях. Общее количество публикаций – 13.
E-mail: Levashov-omsk@mail.ru.
РАСЧЕТ КОНСТРУКЦИЙ МОСТОВЫХ ПРОЛЕТНЫХ СТРОЕНИЙ КОРОБЧАТОГО СЕЧЕНИЯ НА ИЗГИБ С КРУЧЕНИЕМ
С.А. Матвеев, Е.А. Мартынов
Аннотация. Рассмотрены особенности расчета железобетонного пролетного строения коробчатого сечения при изгибе с кручением. Получены компоненты напряженнодеформированного состояния для различных соотношений высоты и ширины поперечного сечения. Установлено, что при увеличении ширины сечения влияние кручения возрастает и схема работы конструкции существенно отличается от балочной.
Ключевые слова: изгиб, кручение, коробчатое сечение.
Введение |
|
стране, так и во всем мире. К таким конструкциям |
Железобетонные коробчатые конструкции по- |
относятся пролетные строения мостов в виде ба- |
|
лучили широкое распространение, |
как в нашей |
|
26 |
Вестник СибАДИ, выпуск 4 (22), 2011 |

СТРОИТЕЛЬСТВО. СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ И ИЗДЕЛИЯ
лок и плит, кессонные фундаменты, отдельные виды плит перекрытий и т.д.
Одной из проблем, с которой сталкиваются проектировщики при расчете коробчатых конструкций, является учет кручения от нагрузки, приложенной с эксцентриситетом.
Основная часть
Кручение в железобетоне представляет собой весьма сложное явление, для описания которого требуется привлечение ряда гипотез, подтвержденных экспериментом. Проблема изгиба с кручением постоянно включается в "Планы важнейших научноисследовательских работ по бетону и железобетону" научно-исследовательских институтов и вузов.
Внастоящее время имеется больше десятка предложений по оценке прочности железобетона при наличии кручения.
Вдействующих нормативных документах присутствует ряд положений, касающихся оценки прочности при наличии кручения, которые, несмотря на имеющийся опыт проектирования, пока освещены недостаточно и не всегда согласуются с реальной работой железобетона. В них отсутствуют целые разделы, например, по определению напряжений в арматуре, воспринимающей нормальные и касательные напряжения; не учитывается снижение предела призменной прочности бетона из-за сложного напряженного состояния; учет нелинейности работы материала и т.д. Характер разрушения конструкции зависит от формы поперечного сечения, схемы поперечного и продольного армирования, а также от вида загружения.
При действии только крутящих моментов в начальной стадии загружения железобетонный элемент работает упруго. В нем возникают касательные, а, следовательно, и главные сжимающие и растягивающие напряжения, ориентированные под углом, близким к 45° по отношению к продольной оси элемента. После того, как удлинения бетона по направлению действия главных растягивающих напряжений достигнут предельных значений, в бетоне образуются развивающиеся по всему контуру сечения диагональные трещины. В реальных конструкциях крутящие моменты действуют, как правило, в сочетании с другими видами усилий, например, изгибающим моментом и поперечной силой. Если значения крутящих моментов невелики, то спиральные трещины развиваются только в зоне, растянутой от совместного действия изгибающего и крутящего моментов. После образования спиральных трещин усилия в направлении главных растягивающих напряжений воспринимает арматура, а усилия, действующие по направлению главных сжимающих напряжений - бетон.
Разрушение железобетонного элемента при совместном действии изгибающего и крутящего моментов происходит, как правило, по сложному сечению вследствие:
- достижения арматурой физического или условного предела текучести с последующим разрушением бетона сжатой зоны;
- достижения поперечной арматурой предела текучести с последующим раздроблением бетона
сжатой зоны; при этом напряжения в продольной арматуре не достигают предела текучести;
-достижения продольной арматурой предела текучести с последующим раздроблением бетона сжатой зоны; при этом напряжения в поперечной арматуре не достигают предела текучести;
-раздробления сжатого бетона, заключенного
вполосах между спиральными трещинами; при этом напряжения в арматуре как поперечной, так и продольной ниже предела текучести.
Существует два основных направления развития методов расчета железобетонных конструкций при действии крутящих моментов.
Первое направление включает расчетную модель "пространственного сечения", второе – расчетную модель пространственной фермы или кар- касно-стержневую модель, предложенную в 20-х годах XX века Е. Раушем.
В общем виде расчетная модель пространственного сечения должна содержать полную систему уравнений, которая связывает статическую, физическую и геометрическую стороны задачи, с привлечением диаграмм деформирования бетона и арматуры максимально приближенных к реальным. Однако практическая реализация модели пространственного сечения в общем виде представляет значительные трудности, в силу чего в нормах используют упрощенные расчетные методы, опирающиеся, главным образом, на эмпирические зависимости.
Экспериментальные исследования показывают, что при разрушении железобетонного элемента по пространственному сечению, в зависимости от значений изгибающего и крутящего моментов, а также наличия и величины поперечной силы возможны три схемы расположения сжатой зоны.
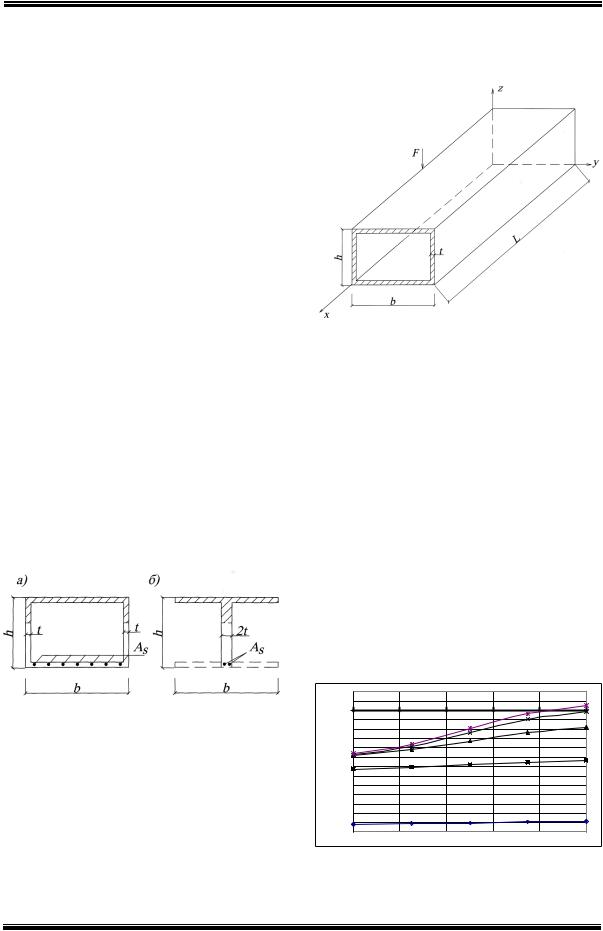
Первая схема (рисунок 1.а) соответствует расположению сжатой зоны у верхней грани элемента и имеет место при воздействии на элемент значительных по величине изгибающего и крутящего моментов.
Рис. 1. Схемы расположения сжатой зоны
Вторая схема (рисунок 1.б) соответствует расположению сжатой зоны у боковой грани и имеет место при воздействии крутящего момента и поперечной силы (изгибающий момент так мал, что его влиянием можно пренебречь).
Третья схема (рисунок 1.в) соответствует расположению сжатой зоны у нижней грани. Такой случай может иметь место в зоне, где действуют небольшие изгибающие моменты, мало влияющие на вид разрушения элемента. При этом площадь
Вестник СибАДИ, выпуск 4 (22), 2011 |
27 |
СТРОИТЕЛЬСТВО. СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ И ИЗДЕЛИЯ
поперечного сечения верхней арматуры, которая попадает в растянутую зону может быть меньше площади нижней арматуры.
Согласно теории Е. Рауша бетонный элемент с ортогональной арматурой, подверженный сдвигу, имеет диагональные трещины, которые разделяют бетон на отдельные центрально сжатые полосы. Вместе с арматурой, работающей на растяжение, они образуют стержневую систему, противодействующую сдвиговым усилиям.
Для упрощения расчетов предполагалось, что диагональные бетонные полосы наклонены под углом 45° к арматуре. В соответствии с предложенной Раушем теорией железобетонный элемент сопротивляется кручению подобно условной трубе, то есть таким образом, что прикладываемый крутящий момент воспринимается потоком касательных напряжений в стенке трубы. Следует отметить, что теория пространственной стержневой системы была разработана на основе анализа результатов опытов, которые показали, что прочность сплошного сечения железобетонного стержневого элемента при кручении приблизительно равна прочности некоторого заменяющего полого сечения.
Отечественные и зарубежные нормы расчета [1-3] коробчатых элементов, работающих на изгиб с кручением, как правило, предполагают балочную схему работы конструкции. При этом в зависимости от граничных условий, одна полка полностью сжата, другая – полностью растянута. Тогда расчет коробчатого сечения сводится к расчету эквивалентного таврового сечения, полка в растянутой зоне во внимание не принимается, а вся арматура в растянутой полке является расчетной (рисунок 2).
Данное исследование проводится для проверки принятых в нормативных документах гипотез и методов расчета при проектировании конструкций мостовых пролетных строений произвольного размера при изгибе с кручением.
Рис. 2. Замена коробчатого сечения тавром: а) исходная схема; б) эквивалентная схема
Для первоначальных исследований была выбрана задача определения напряженнодеформированного состояния шарнирно опертой по двум краям конструкции коробчатого сечения нагруженной сосредоточенной силой, которая приложена в середине пролета над одной из вертикальных стенок (рисунок 3).
Для расчетов приняты следующие исходные данные: длина L = 30 м, высота сечения h = 1 м, толщина стенки t = 10 см, материал – бетон класса В35 (модуль упругости Е = 34500 МПа, коэффициент Пуассона = 0,2), сила F = 100 кН, балка за-
креплена шарнирно на опорах, собственный вес не учитывается. Ширина конструкции b варьировалась от h (балочная схема) до 10h (плита).
Рис. 3. Расчетная схема
В данном варианте задачи влияние армирования на напряженно-деформированное состояние конструкции не учитывалось, материал принят изотропным и упругим.
Расчет выполнялся численно методом конечных элементов. Во избежание ошибок вычисления проводились в двух программных комплексах: "ЛИРА" и "MIDAS".
Конструкция аппроксимирована пластинчатыми элементами оболочки размером в плане 0,25х0,25 м. Граничные условия задачи:
v = w = v/ x = 0 при х = 0, z = 0, что соответствует шарнирно-подвижной опоре;
u = v = w = v/ x = 0 при х = L, z = 0, что соответствует шарнирно-неподвижной опоре.
В результате расчетов определены перемещения, усилия, напряжения и траектории главных напряжений в конструкции.
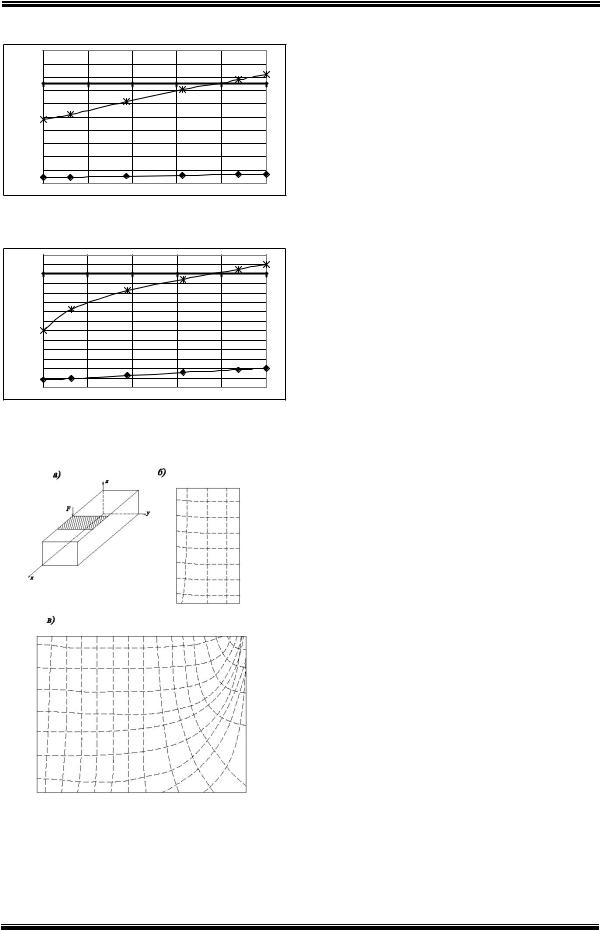
На рисунках 4-7 приведены графики изменения прогибов, нормальных напряжений х и траекторий главных напряжений на верхней грани при различных соотношениях h/b. Знак минус на эпюре прогибов соответствует выгибу конструкции.
|
-4 |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 5 |
|
-2 |
||||||
|
0 |
|
|
|
|
|
x/b |
|
2 |
|
|
|
|
|
4 |
|
4 |
|
|
|
|
|
3 |
|
6 |
|
|
|
|
|
|
мм |
8 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
w, |
12 |
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
22 |
|
|
|
|
|
1 |
|
24 |
|
|
|
|
|
|
|
26 |
|
|
|
|
|
|
Рис. 4. Эпюры прогибов верхней полки
всередине пролета:
1– при h/b=1; 2 – при h/b=2,5; 3 – при h/b=5; 4 – при h/b=7,5; 5 – при h/b=10
28 |
Вестник СибАДИ, выпуск 4 (22), 2011 |
СТРОИТЕЛЬСТВО. СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ И ИЗДЕЛИЯ
|
1.0 |
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
2 |
|
0.2 |
|
|
|
|
|
|
|
|
|
|
|
|
x/b |
|
|
-0.2 |
|
|
|
|
|
|
|
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
МПа |
-0.6 |
|
|
|
|
|
|
-1.0 |
|
|
|
|
|
|
|
х, |
|
|
|
|
|
|
|
-1.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1.8 |
|
|
|
|
|
|
|
-2.2 |
|
|
|
|
|
|
|
-2.6 |
|
|
|
|
|
1 |
|
-3.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5. Эпюра х в верхней полке в середине |
|||||||
|
|
пролета: 1 – при h/b=1; 2 – при h/b=10 |
|
||||
|
1.0 |
|
|
|
|
|
2 |
|
0.5 |
|
|
|
|
|
|
|
0.0 |
|
|
|
|
|
x/b |
|
-0.5 |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
-1.0 |
|
|
|
|
|
|
МПа |
-1.5 |
|
|
|
|
|
|
-2.0 |
|
|
|
|
|
|
|
-2.5 |
|
|
|
|
|
|
|
х, |
-3.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-3.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-4.0 |
|
|
|
|
|
|
|
-4.5 |
|
|
|
|
|
1 |
|
-5.0 |
|
|
|
|
|
|
|
-5.5 |
|
|
|
|
|
|
|
-6.0 |
|
|
|
|
|
|
Рис. 6. Эпюра х в верхней полке при x = L/4: |
|||||||
|
|
|
1 – при h/b=1; 2 – при h/b=10 |
|
|||
Рис. 7. Траектории главных напряжений в верхней полке:
а) расчетная схема; б) при h/b=1; в) – при h/b=10
Заключение
Анализ полученных результатов позволяет сделать следующие выводы:
1.При балочной схеме конструкции (h=b) вся верхняя полка испытывает сжатие, нижняя – растяжение. Нейтральная линия практически совпадает с осью симметрии. Влияние крутящего момента на величину нормальных напряжений и перемещений невелико, крен между крайними точками сечения не превышает 2,5 %.
2.При увеличении ширины элемента разница прогибов и напряжений в крайних точках сечения увеличивается, нулевая линия поворачивается относительно оси.
3.При балочной схеме работы траектория главных напряжений практически ортогональна граням конструкции. В данном случае полностью оправдано применение продольной и поперечной арматуры в виде прямоугольных сеток, уложенных вдоль граней, а расчет может проводиться по эквивалентной схеме в виде тавра.
4.При определенном соотношении b и h (в
нашем случае b 9,16h) верхняя (нижняя) полка и стенки испытывают разнознаковые напряжения. Следовательно, такие конструкции при расчете приводить к тавровому сечению не допустимо.
5. Траектория главных напряжений при плитной работе конструкции существенно отличается от балочной схемы. Расчет рационального армирования в данном случае вызывает значительные затруднения. Следует учитывать так же, что нагрузка является подвижной, т.е. траектории главных напряжений зависят не только от величины силы, но и от ее местоположения.
Полученные данные показывают, что методики расчета, заложенные в нормативных документах справедливы только для балочных конструкций. При переходе от балочной схемы работы к плитной происходит качественное изменение характера напря- женно-деформированного состояния конструкции.
Для развития теории расчета коробчатых железобетонных конструкций необходимо изучить границы применимости различных методов расчета, на которые будут влиять соотношения геометрических размеров, величин изгибающих и крутящих моментов. Необходим учет схем армирования и нелинейности материалов на напряженно-деформированное состояние конструкции.
Библиографический список
1.СП 35.13330.2011. "СНиП 2.05.03-84. Мосты
итрубы. Актуализированная редакция".
2.СП 52-101-2003. Бетонные и железобетонные конструкции без предварительного напряжения арматуры.
3.EN 1992-2. Eurocode 2. Design of concrete structures - Concrete bridges - Design and detailing rules.
THE CALCULATION OF BRIDGE STRUCTURES WITH BOX-SHAPED CROSS SECTION AT A BEND WITH TORSION
S.A. Matveev, E.A. Martynov
Вестник СибАДИ, выпуск 4 (22), 2011 |
29 |

СТРОИТЕЛЬСТВО. СТРОИТЕЛЬНЫЕ МАТЕРИАЛЫ И ИЗДЕЛИЯ
Features of calculation of a concrete bridge struc- |
вание и расчет слоистых дорожных конструкций; |
tures with box-shaped cross section are considered at |
геосинтетические материалы в строительстве. |
a bend with torsion. Components of the intense- |
Общее количество опубликованных работ: 115. |
deformed condition for various parities of height and |
Е-mail: matveev_sa@sibadi.org |
width of section are received. |
Мартынов Евгений Анатольевич - кандидат |
|
|
Матвеев Сергей Александрович - доктор |
технических наук, доцент. Основные направления |
технических наук, профессор кафедры «Строи- |
научной деятельности Расчет конструктивно- |
тельная механика». Основные направления науч- |
анизотропных конструкций. Общее количество |
ных исследований – математическое моделиро- |
опубликованных работ: 50 |
УДК 656
ВЫСОЛООБРАЗОВАНИЕ В КОНСТРУКЦИЯХ СТРОИТЕЛЬНЫХ ОБЪЕКТОВ
В.П. Михайловский, В.С. Прокопец
Аннотация. Выявлены основные причины, способствующие образованию высолов на стенах зданий и тротуарных плитках. Проведено натурное наблюдение с фотофиксацией различных видов высолов, с установлением причин их возникновения. Проведен ренгенофазовый анализ образовавшихся высолов. Даны конкретные предложения по предупреждению высолообразования.
Ключевые слова: высолы, натурные наблюдения, причины и предупреждение высолообразования.
Введение
Архитектурная выразительность является одним из важнейших критериев при выборе материалов для возведения строительных объектов, их отделки и облагораживания прилегающих к ним территорий. Одним из недостатков таких материалов является появление высолов (выцветов) на поверхности.
Высолы понимаются как образование белых налетов (отложений) на поверхности и внутри материала. Выцветы характерны для цветных растворов и бетонов, и здесь процесс высолообразования может идти с явлением осветвления оксидов пигментов, применяемых цветных цементов, и появлением на поверхности светлых пятен. Материалы статьи посвящены в основном высолообразованию. Высолы не только портят внешний вид объектов, но и разрушают их.
Причины высолообразования
1.Наиболее распространенной причиной появления высолов является гидролитический распад некоторых минералов портландцементного клинкера в процессе твердения с выделением значительного количества гидроксида кальция в свободное состояние. Уже в начальной стадии процесса гидратации цемента происходит быстрое взаимодействие алита с водой с образованием гидросиликата кальция и гидроксида:
2(3CaO SiO2 ) 6H2O
3CaO 2SiO2 3H2O 3Ca(OH )2
Белит гидратируется медленнее алита и при его взаимодействии с водой выделяется меньше
Ca(OH)2 ,что видно из уравнения химической реакции:
2(2CaO SiO2 ) 4H2O
3CaO 2SiO2 3H2O Ca(OH )2
Об объемах выделяющегося гидроксида кальция можно судить по тому, что алита в портландцементном клинкере содержится порядка 45…60%, а белита – 20…30%, поэтому гидроксида образуется около 15% от массы цемента.
С целью выяснения характера и возможных причин высолообразования были отобраны образцы цементно-песчаного покрытия стен и образовавшихся на них высолов. Данные образцы отобраны с одного, наиболее характерного здания в районе элитной застройки «Старгород» г.Омска. Рентгенофазовый анализ состава отобранных образцов показал наличие следующих фаз (рисунки 1,2).
Высолы содержат значительное количество кварца SiO2 (ICDD 46-1045), сульфата натрия
Na2SO4 (ICDD 37-1465), K3Na(SO4)2 (ICDD 20-928)
и кальцита CaCO3 (ICDD 5-586). По данным химического состава в них присутствуют также Na, Fe, S, Ca, K.
Анализы выполненных физико-химических исследований данного объекта показывают, что по химическому составу образовавшиеся на поверхности цементно-песчаного раствора высолы можно отнести к двум разновидностям: карбонатнокальциевым и сульфатно-натриевым.
30 |
Вестник СибАДИ, выпуск 4 (22), 2011 |
